1. 
   является аналитической в области ;
   
2. 
   ;
   
3. 
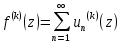   Ряд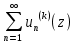 сходится равномерно в любой замкнутой подобласти области .
   

10. Степенные ряды. Теорема Абеля.11. Радиус и круг сходимости. Следствия из теоремы Абеля. Ряд вида ∑(????−????0)????∞????=0.Область 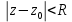называется кругом сходимости, а число 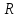радиусом сходимости степенного рядаСледствия из теоремы Абеля.

1. 
   Если степенной ряд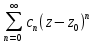 расходится в некоторой точке 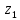, то он расходится для всех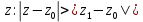
   
2. 
   Для любого степенного ряда существует такое число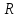 , что внутри круга 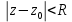ряд сходится, а вне этого круга расходится. В круге 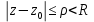ряд сходится абсолютно.
   

Замечание. 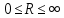. При 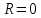степенной ряд сходится лишь в точке . При 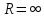ряд сходится в любой точке

3. 
   Внутри круга сходимости степенной ряд сходится к аналитической функции.
   
4. 
   Степенной ряд внутри круга сходимости можно почленно интегрировать и дифференцировать любое число раз, причём радиус сходимости полученных рядов равен радиусу сходимости исходного ряда.
   
5. 
   Коэффициенты степенного ряда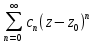 находятся по формулам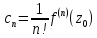
   
6. 
   Радиус сходимости степенного ряда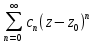 находится по формулам:
   

---

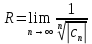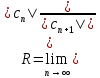
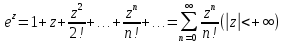
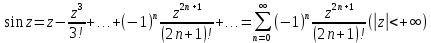
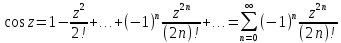
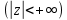
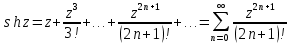
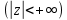
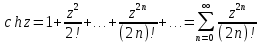
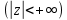
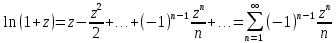
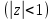
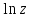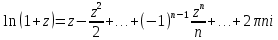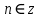
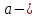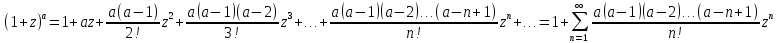
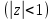
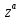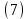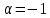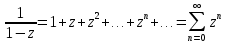
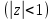
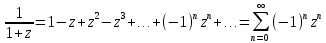
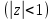
или 12. Ряд Тейлора. Разложение аналитической в круге функции в ряд Тейлора.13. Разложение элементарных функций комплексной переменной в ряд Тейлора.1) 2) 3) 4) 5) 6) Здесь – главная ветвь логарифма для многозначной функции, где 7) это альфа Здесь - главная ветвь степенной функции8) Частный случай разложения : при получим бесконечную геометрическую прогрессию 14. Нули аналитической функции. Примеры.

---

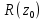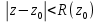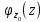15. Правильные и особые точки аналитической функции.Опред. Точка называется правильной точкой для аналитической в области функции , если существует степенной ряд с радиусом сходимости такой, что в общей части круга сходимости и области сумма этого ряда совпадает с . Точки, не являющиеся правильными, называются особыми.Опред. Точка называется изолированной собой точкой функции , если однозначная аналитическая функция в кольце 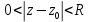, а 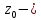особоая точка.Классификация изолированных особых точек

1. 
   Устранимая особая точка
   

Опред. Изолированная особая точка называется устранимой особой точкой, если существует конечный предел 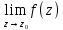Теорема 1 Для того чтобы точка была устранимой особой точкой функции , необходимо и достаточно, чтобы ряд Лорана функции в точке не содержал главной части (то есть все коэффициенты 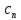с отрицательными номерами равны 0)

2. 
   Полюс
   

Опред. Изолированная особая точка

---

называется полюсом, если предел

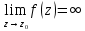
Для того чтобы точка была полюсом функции , необходимо и достаточно, чтобы эта точка была нулём для функции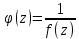

Точку называют полюсом n-го порядка для функци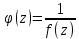и . При 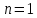полюс называют простым.

Для того чтобы точка была полюсом n-го порядка функции , необходимо и достаточно, чтобы функцию можно было представить в ви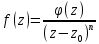де , где 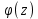аналитична в точке и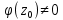

Теорема 2.

Для того чтобы точка была полюсом n-го порядка функции , необходимо и достаточно, чтобы главная часть ряда Лорана функции в точке имела конечное число членов, не более 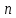, причём 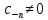, то есть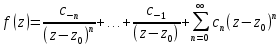

3. 
   Существенно особая точка
   

Опред. Изолированная особая точка называется существенно особой точкой, если не существует.Теорема 3

---

Для того чтобы точка была полюсом n-го порядка функции , необходимо и достаточно, чтобы главная часть ряда Лорана функции в точке содержала бесконечно много членов.Замечание. Исследование характера бесконечно удалённой точки удобно проводить заменой 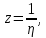при этом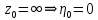 16. Ряд Лорана. Область сходимости ряда Лорана. Разложение аналитической функции в ряд Лорана.17. Устранимая особая точка. Полюс m-го порядка. Существенно особая точка. Определение характера особой точки по главной части ряда Лорана.Если что вопрос 19

1. 
   Устранимая особая точка
   

Опред. Изолированная особая точка называется устранимой особой точкой, если существует конечный предел Теорема 1 Для того чтобы точка была устранимой особой точкой функции , необходимо и достаточно, чтобы ряд Лорана функции в точке не содержал главной части (то есть все коэффициенты с отрицательными номерами равны 0)

2. 
   Полюс
   

Опред. Изолированная особая точка называется полюсом, если предел Для того чтобы точка была полюсом функции , необходимо и достаточно, чтобы эта точка была нулём для функции

---

Смотрите также файлы

• Характеристика торгового предприятия.doc

• Брак и семья.doc

• Итоговая работа по обж за курс 9 класса. Рекомендованное время выполнения 15 минут.docx

• 3. Experience is the best teacher. Let me share my opinion about the statement Experience is the best teacher.docx

• Вопросник по вт.docx