Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

Московский технический университет связи и информатики

Кафедра теории электрических цепей

Курсовая работа 1

по дисциплине «Теоретические основы электротехники»

Вариант 23


Выполнил студент группы БИН2107 Толканова Т.А.
Проверил: пр. Елисеев С.Н.

Москва 2022

ЗАДАЧА 1. РАСЧЕТ РЕЗИСТИВНЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА



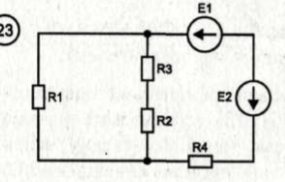
Рисунок 1- Схема цепи





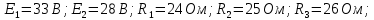
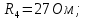
1.2.Метод уравнений Кирхгофа



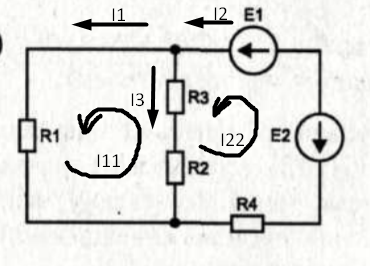
Рисунок 2- Расписанная схема цепи

В схеме два узла, а значит нужно одно уравнение по первому закону Кирхгофу. Первый закон гласит, что сумма токов сходящихся в узле равна нулю. Принято считать, что входящие токи являются положительными, а выходящими отрицательными.  Исходя из этих условий, уравнение для данной цепи имеет такой вид 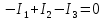(1):

(1)
На схеме два контура, следовательно, будет два уравнения по второму закону Кирхгофу. Направления обхода для двух контуров выбраны против часовой стрелки.

В первом контуре ток 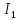совпадает с направлением обхода контура - падение напряжения положительное. Ток 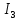не совпадает, таким образом, падение напряжения будет отрицательным. В первом контуре отсутствует источник ЭДС и это значит, что сумма падений напряжений будет равно нулю.

---

Уравнение для первого контура 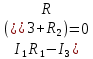(2):
(2)

Во втором контуре ток 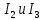совпадают с направлением обхода контура из этого можно сделать вывод, что падения напряжений будут положительными. Обход контура против часовой стрелки значит, ЭДС 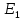будет со знаком плюс, так как совпадает с направлением, а ЭДС 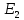будет со знаком минус, так как он не совпадает с направлением.

Уравнение для второго контура 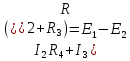(3):
(3)
Все эти три уравнения образуют систему 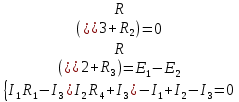(4): 
(4)
Решение методом подстановки 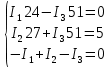(5):

(5)

Ответы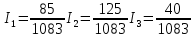: (6)

(6)

1.3. Метод контурных токов



Рисунок 3- Расписанная схема цепи

Направления обхода для двух контуров выбраны против часовой стрелки.

Контурных токов два, тогда получаем два уравнения.

Первое уравнение будет состоять из контура 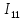умноженного на сумму сопротивлений входящих в данный контур, а затем вычитаем ток 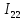умноженного на сумму общих сопротивлений первого и второго контуров. Данное выражение будет равняться 0, так как отсутствует источник ЭДС. Уравнение для первого контура 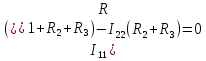(7):
(7)

Второе уравнение будет состоять из контура 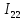умноженного на сумму сопротивлений входящих в данный контур, а затем вычитаем ток 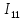умноженного на сумму общих сопротивлений первого и второго контуров. Данное выражение будет равняться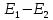

---

. ЭДС будет положительным, потому что направление обхода (против часовой стрелки) совпадает с направление ЭДС, в противном случае ЭДС должен быть отрицательным. Уравнение для второго контура 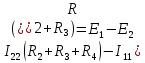(8):
(8)
Все эти два уравнения образуют систему 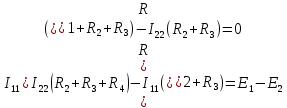(9): 
(9)

Контурный ток равен действительному току, который принадлежит только этому контуру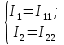. (10)

(10)

Токи, протекающие через общие сопротивления определяем, как алгебраическую сумму контурных токов, учитывая направление обхода.  Например, через резисторы 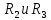 протекает ток , его направление совпадает с направлением обхода второго контура и противоположен направлению первого контура. Значит, для него выражение будет выглядеть (11)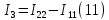



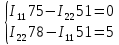
Решение методом подстановки 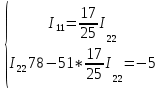(12):



(12)

Ответы 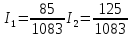(13):

(13)



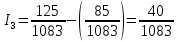
1.5. Метод двух узлов



Проводимости ветвей 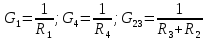(14)

(14)

Составим узловое уравнение для узла 1. Знак ЭДС определяется её направлением, если к узлу, то положительное, если от узла – отрицательное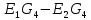. (15)

(15)

Определим напряжение 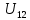. В числителе будет алгебраическая сумма токов в знаменатели сумма проводимости 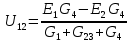(16)

(16)

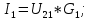
Найдем токи в ветвях. Если направление ЭДС совпадает с направление напряжения, то берем напряжение со знаком плюс. В противном случае со знаком минус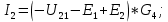. (17)

---

(17)



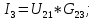
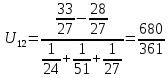
Решение методом подстановки 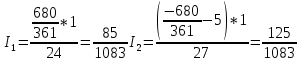(18)



(18)



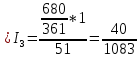
1.6. Метод наложения

В цепи два источника, поэтому разложим его на две схемы. В каждой с помощью закона Ома найдём токи этих подсхем.

Составим частную схему с первым источником ЭДС и рассчитаем частные токи в ней, убрав второй источник.



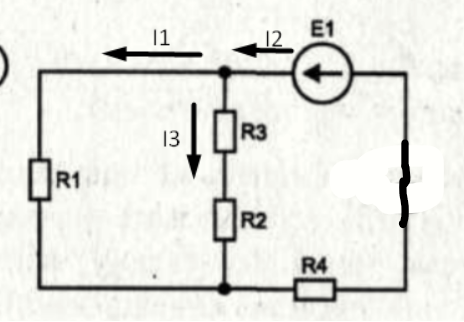
Рисунок 4 – Первая подсхема

Найдем ток по закону Ома для полной цепи 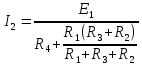(19)

(19)

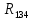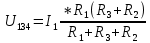Найдем напряжение на (20)

(20)

Тогда то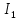к и ток 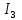равены 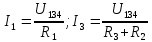(21)

(21)

Составим частную схему со вторым источником ЭДС 



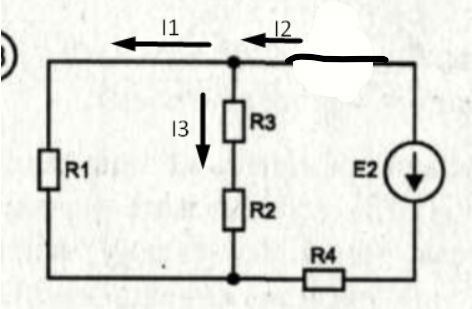
Рисунок 5 – Вторая подсхема

Найдем ток по закону Ома для полной цепи 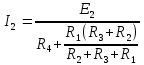(22)

(22)

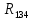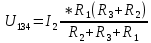Найдем напряжение на (23)

(23)

Тогда то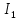к и ток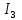 равены (24)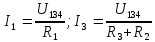

---

(24)

Найдем токи в исходной цепи, для этого просуммируем частичные токи, учитывая их направление. Если направление частичного тока совпадает с направлением исходного тока, то берем со знаком плюс, в противном случае со знаком минус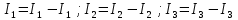.(25)

(25)

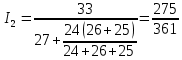
Решение методом подстановки. Для первой цепи 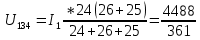(26)



(26)



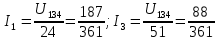
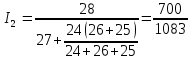
Решение методом подстановки. Для второй цепи 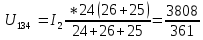(27)



(27)



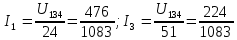
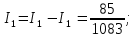
Токи в исходной цепи 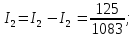(28):



(28)



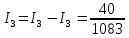
1.7. Рассчитать ток в сопротивление R1 методом эквивалентного генератора ЭДС



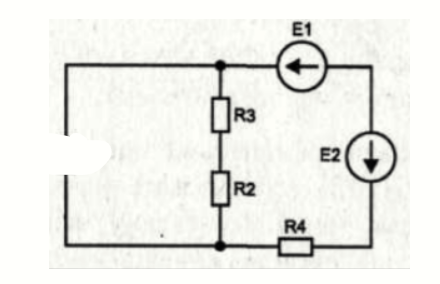
Рисунок 6 – Вторая подсхема

Находим эквивалентное сопротивление (29)



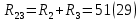
Находим эквивалентное сопротивление ЭДС (30)



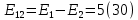
Произвольно задаем E эк (31)



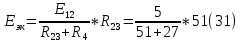
Находим эквивалентное сопротивление (32)



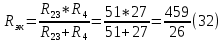
Находим ток пустой цепи (33)



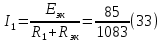
ЗАДАЧА 2. РАСЧЕТ РАЗВЕТВЛЕННЫХ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА



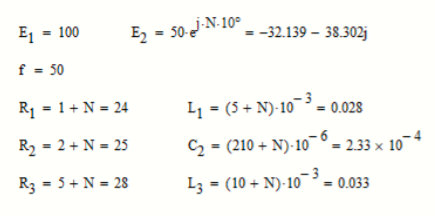
Рисунок 7 - Сопротивления реактивных элементов



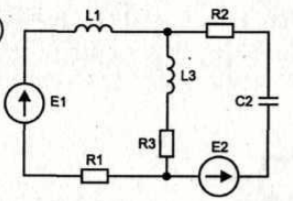
Рисунок 8 – Схема цепи

Найдем сопротивления реактивных элементов:

---

Смотрите также файлы

• 2е задание 10 баллов психологический анализ ситуации. Задние Заполните Таблицу 1, кратко представьте основные этапы трансформации предмета психологии от души до психики. Цель.rtf

• ож 616. 002. 197 Мтар 76. 29. 55.docx

• Приобретенные пороки клапанов сердца.docx

• Название Дата.docx

• Глобальная компьютерная сеть Internet.docx