Файл: Курсовая работа 1 по дисциплине Теоретические основы электротехники.docx
Добавлен: 09.11.2023
Просмотров: 138
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
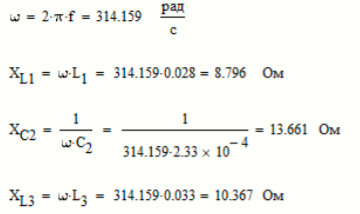
Рисунок 9.1 - Сопротивления реактивных элементов
Найдем сопротивления ветвей:
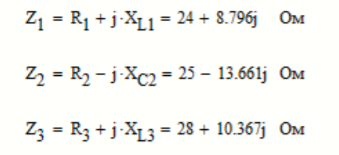
Рисунок 9.2 - Сопротивления ветвей
2.2. Метод уравнений Кирхгофа
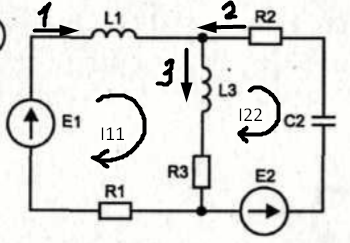
Рисунок 10 - Схема цепи
В схеме два узла, а значит нужно одно уравнение по первому закону Кирхгофу. Первый закон гласит, что сумма токов сходящихся в узле равна нулю. Принято считать, что входящие токи являются положительными, а выходящими отрицательными. Исходя из этих условий, уравнение для данной цепи имеет такой вид (34):
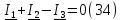
На схеме два контура, следовательно, будет два уравнения по второму закону Кирхгофу. Направления обхода для двух контуров выбраны по часовой стрелки.
В первом контуре ток
совпадает с направлением обхода контура - падение напряжения положительное. Ток 
совпадает, таким образом, падение напряжения будет положительным. В первом контуре источник ЭДС будет положительным. Уравнение для первого контура (36):
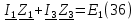
Во втором контуре ток
не совпадают с направлением обхода контура из этого можно сделать вывод, что падения напряжений будут отрицательным. Обход контура по часовой стрелки значит, ЭДС
будет со знаком минус, так как не совпадает с направлением. Уравнение для второго контура (37):
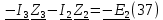
Все эти три уравнения образуют систему 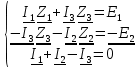(38):
(38)Вычисления комплексных токов в Mathcad с помощью обратной матрицы:
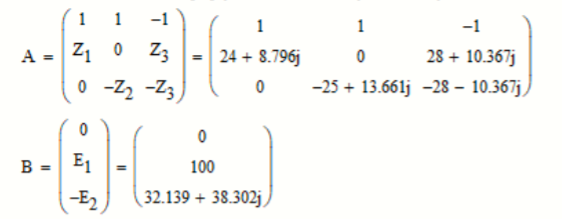
Рисунок 11 – Система уравнений через матрицы
Решая систему, получаем токи:
Рисунок 12 – Ответы
Векторная диаграмма токов:
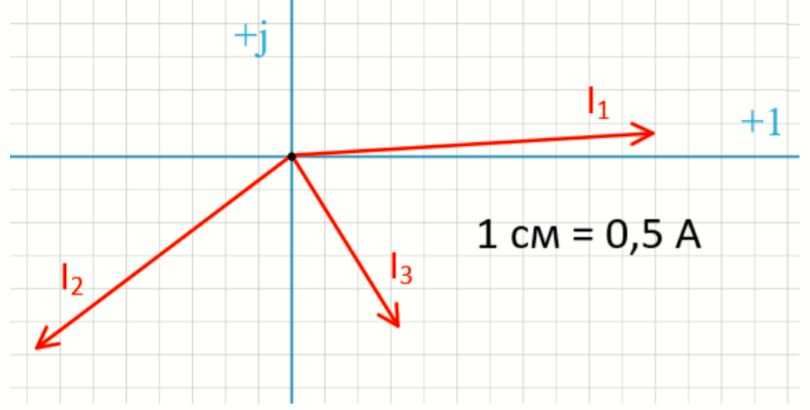
Рисунок 13- Векторная диаграмма токов
2.3. . Метод контурных токов
Рисунок 14 - Схема цепи
Направления обхода для двух контуров выбраны по часовой стрелки.
Контурных токов два, тогда получаем два уравнения.
Первое уравнение будет состоять из контура
умноженного на сумму сопротивлений входящих в данный контур, а затем вычитаем ток 
умноженного на сумму общих сопротивлений первого и второго контуров. Данное выражение будет равняться положительному 
, так как ЭДС совпадает с направлением. Уравнение для первого контура (39):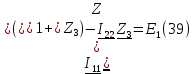 
Второе уравнение будет состоять из контура
умноженного на сумму сопротивлений входящих в данный контур, а затем вычитаем ток умноженного на сумму общих сопротивлений первого и второго контуров. Данное выражение будет равняться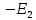 
, так как ЭДС не совпадает с направлением с направлением обхода контура. Уравнение для второго контура (40):
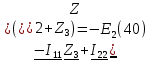
Все эти два уравнения образуют систему 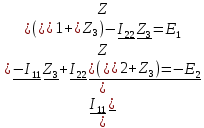(41):
(41)Контурный ток равен действительному току, который принадлежит только этому контуру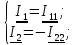. (42)
(42)Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода. Например, через резисторы
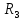протекает ток , его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть (43)
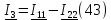
Вычисления комплексных токов в Mathcad через обратную матрицу:
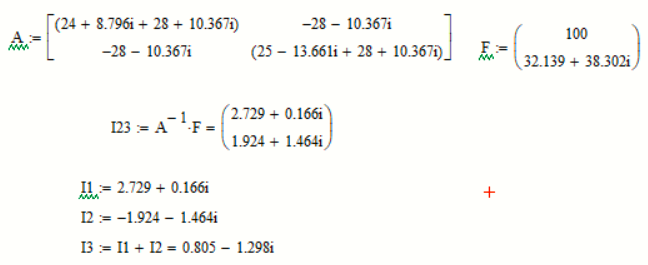
Рисунок 15-Вычисления в Mathcad
2.4. Метод узловых потенциалов
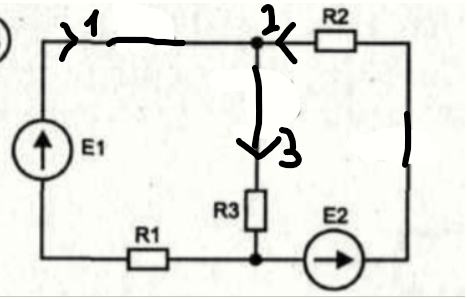
Рисунок 16- Цепь
Проводимости ветвей. (44)
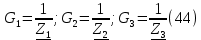
Составим уравнения по первому закону Кирхгофа для узла 1. (45)
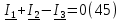
Используя обобщённый закон Ома составим уравнения для нахождения каждого из токов.(46)
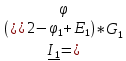
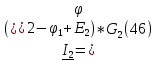
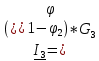
Подставим полученные выражения для токов в уравнения (47)
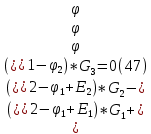
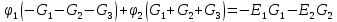
Вычисления комплексных токов в Mathcad по методу узловых потенциалов:
Рисунок 17 – Вычисления в Mathcad
2.6. Метод наложения
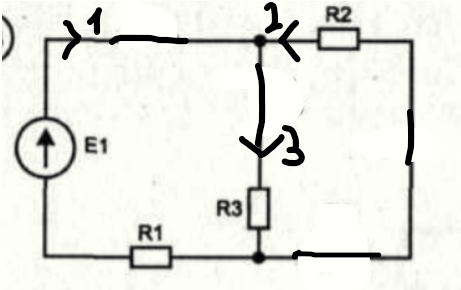
Рисунок 18 - Первая подсхема
В цепи два источника, поэтому разложим его на две схемы. В каждой с помощью закона Ома найдём токи этих подсхем.
Составим частную схему с первым источником ЭДС и рассчитаем частные токи в ней, убрав второй источник.
Найдем ток по закону Ома для полной цепи (48)
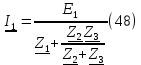
Найдем напряжение на
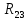(49)
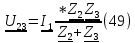
Тогда ток
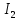и ток 
равены (50)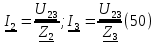
Составим частную схему со вторым источником ЭДС
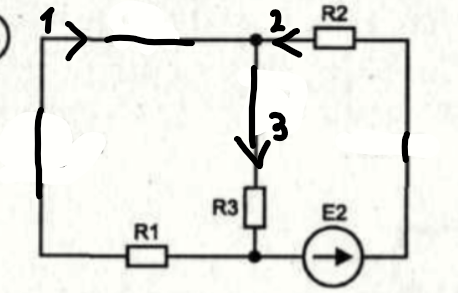
Рисунок 19 - Вторая подсхема
Найдем ток по закону Ома для полной цепи (51)
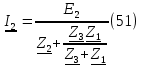
Найдем напряжение на
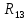(52)
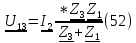
Тогда ток
и ток равены (53)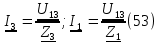
Найдем токи в исходной цепи, для этого просуммируем частичные токи, учитывая их направление. Если направление частичного тока совпадает с направлением исходного тока, то берем со знаком плюс, в противном случае со знаком минус.(54)
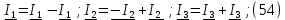
Вычисления комплексных токов в Mathcad по методу наложения:
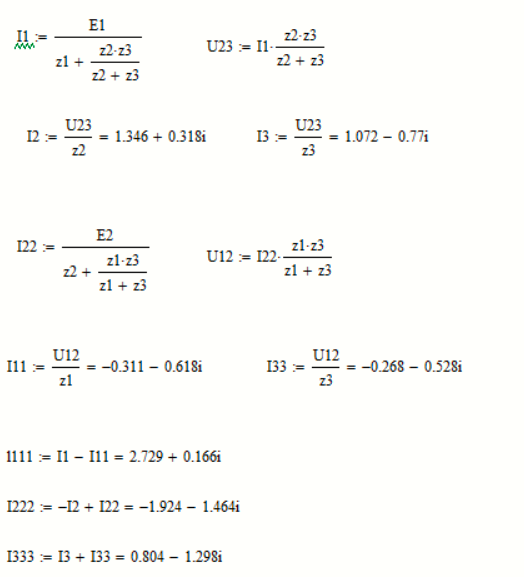
Рисунок 20 – Вычисления в Mathcad
2.7. Рассчитать ток в сопротивление R1 методом эквивалентного генератора ЭДС
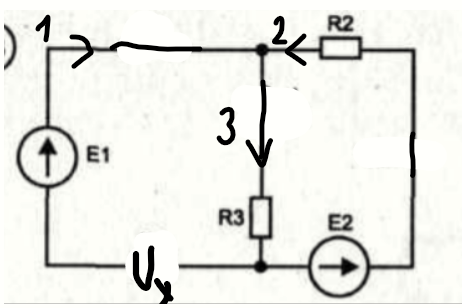
Рисунок 21 – Схема без R1
Произвольно задаем E эк (55)
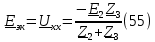
Находим эквивалентное сопротивление (56)
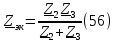
Находим ток пустой цепи (57)
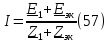
Вычисление в Mathcad тока на
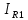используя метод подстановки:
Рисунок 22 – Вычисления в Mathcad
Кривая изменения найденного тока во времени:
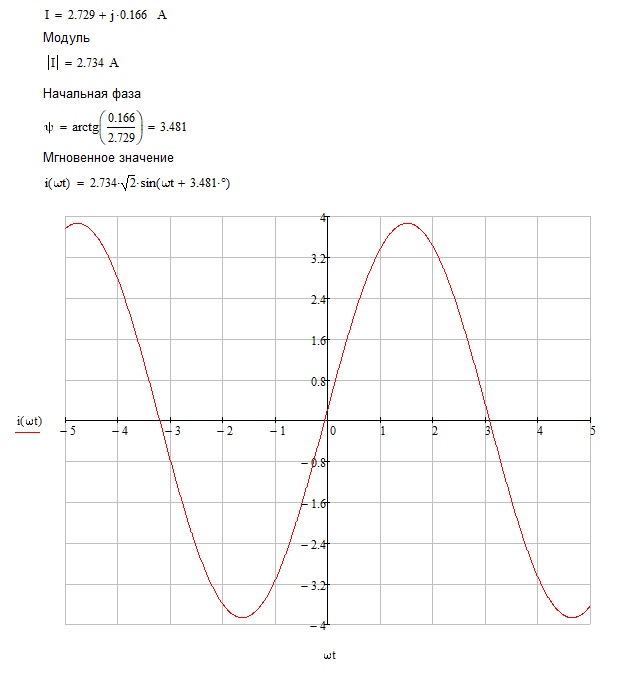
Рисунок 23 – Кривая изменения найденного тока во времени
2.9. Баланс комплексных мощностей
Баланс мощностей (58):
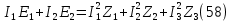
Вычисление баланса мощностей в Mathcad:
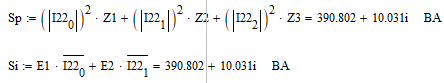
Рисунок 24 – Вычисления в Mathcad