Файл: Вихревое электрическое поле электрическое поле, порождаемое переменным магнитным полем.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 52
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Билет 11
Вихревое электрическое поле — электрическое поле, порождаемое переменным магнитным полем.
Согласно закону Фарадея, возникновение ЭДС электромагнитной индукции возможно и в случае неподвижного контура, находящегося в переменном магнитном поле. Однако сила Лоренца на неподвижные заряды не действует и привести их в движение не может. Поэтому с помощью силы Лоренца нельзя объяснить возникновение ЭДС индукции в неподвижном контуре, в отличие от контуров, движущихся в магнитном поле.
Максвелл для объяснения ЭДС индукции в неподвижном проводнике предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, которое и является причиной возникновения индукционного тока в проводнике.
Согласно этой теории в пространстве, в котором изменяется магнитное поле, непременно возникает электрическое поле с замкнутыми линиями индукции, при этом вектор индукции магнитного поля В в каждое точке пространства перпендикулярен вектору напряженности Ё созданного им электрического поля. Такое поле называют вихревым электрическим полем.
Электромагнитное поле - это фундаментальное физическое поле, взаимодействующее с электрически заряженными телами, представимое как совокупность электрического и магнитного полей, которые могут при определенных условиях порождать друг друга. Электромагнитное поле (его изменение со временем) описывается в электродинамике в классическом приближении посредством системы уравнений Максвелла. При переходе от одной инерциальной системы отсчета к другой электрическое и магнитное поле в новой системе отсчета - каждое зависит от обоих - электрического и магнитного - в старой, и это еще одна из причин, заставляющая рассматривать электрическое и магнитное поле как проявления единого электромагнитного поля.
Ток смещения, или абсорбционный ток — величина, прямо пропорциональная скорости изменения электрической индукции. Это понятие используется в классической электродинамике. Введено Дж. К. Максвеллом при построении теории электромагнитного поля. Введение тока смещения позволило устранить противоречие в формуле Ампера для циркуляции магнитного поля, которая после добавления туда тока смещения стала непротиворечивой и составила последнее уравнение, позволившее корректно замкнуть систему уравнений (классической) электродинамики. Существование тока смещения также следует из закона сохранения электрического заряда. Строго говоря, ток смещения не является электрическим током, но измеряется в тех же единицах, что и электрический ток.
Уравнения Максвелла
В данные уравнения входят 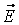 - напряженность электрического поля,
- напряженность электрического поля, 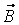 индукция магнитного поля. Эти величины являются основными, т.к. определяют силу, действующую на заряженную частицу (Fл) – силу Лоренца.
индукция магнитного поля. Эти величины являются основными, т.к. определяют силу, действующую на заряженную частицу (Fл) – силу Лоренца.
Входят две вспомогательные величины 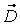 - индукция электрического поля и
- индукция электрического поля и 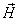 - напряженность магнитного поля. Также входят
- напряженность магнитного поля. Также входят 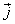 - плотность тока и ρ - плотность заряда.
- плотность тока и ρ - плотность заряда.
Уравнения Максвелла позволяют по известному полю найти токи и заряды (достаточно просто), а также по известным токам и зарядам найти поле (сложно). Уравнения будем писать в СИ в порядке указанном в физической энциклопедии.
Интегральная форма
I уравнение представляет собой обобщение закона полного тока.
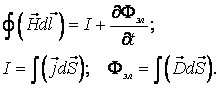
2 уравнение обобщает закон электромагнитной индукции.
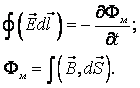
3 теорема Гаусса для электрической индукции.
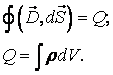
4 уравнение: закон Гаусса для индукции магнитного поля.
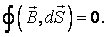
Дифференциальная форма
Используя формулы Остроградского-Гаусса и Стокса можно получить
I уравнение Максвелла.
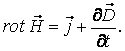
II уравнение Максвелла.
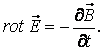
III уравнение Максвелла.
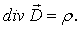
IV уравнение Максвелла
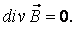
Материальные уравнения
В систему уравнений Максвелла входят 16 скалярных функций координат и времени. Самих уравнений – 8.
Чтобы замкнуть эту систему, используют материальные уравнения.
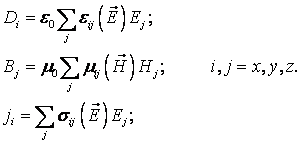
Величины e, μ, σ получаются из других разделов физики или определяются экспериментально.
Закон сохранения энергии
Полная механическая энергия замкнутой системы тел остается неизменной
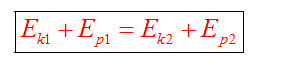

Закон сохранения энергии можно представить в виде
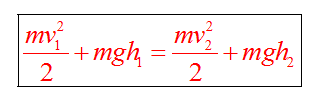
Если между телами действуют силы трения, то закон сохранения энергии видоизменяется. Изменение полной механической энергии равно работе сил трения
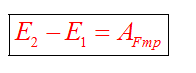
Плотность энергии электромагнитного поля.
Электромагнитные волны переносят энергию из одной точки пространства в другую за конечное время из-за конечности скорости распространения электромагнитной волны, равной , как мы убедились выше, скорости света в той среде, где она распространяется.
Энергия 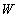 электромагнитной волны внутри некоторого объёма
электромагнитной волны внутри некоторого объёма 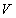 определяется плотностью энергии
определяется плотностью энергии 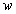 электромагнитного поля волны в соответствии с выражением1:
электромагнитного поля волны в соответствии с выражением1:
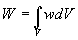 .
.
Оказывается, плотность энергии электромагнитной волны находится в связи с плотностью потока энергии, импульса, связанных с феноменом давления электромагнитных волн.
Вектор Пойнтинга (также вектор Умова-Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
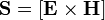
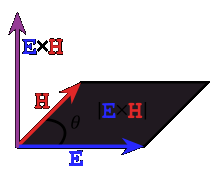 , где E и H — вектора напряжённости электрического и магнитного полей соответственно.
, где E и H — вектора напряжённости электрического и магнитного полей соответственно.
Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии волны.
Поскольку тангенциальные к границе раздела двух сред компоненты E и H, то вектор S непрерывен на границе двух сред.
в комплексной форме:
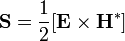 где E и H — вектора комплексной амплитуды электрического имагнитного полей соответственно.
где E и H — вектора комплексной амплитуды электрического имагнитного полей соответственно.
Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии волны.
В силу симметричности тензора энергии-импульса, все три компоненты вектора пространственной плотности импульса электромагнитного поля равны соответствующим компонентам вектора Пойнтинга, делённым на квадрат скорости света: 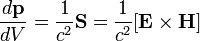 (в системе СИ)
(в системе СИ)
В этом соотношении проявляется материальность электромагнитного поля.
Поэтому, чтобы узнать импульс электромагнитного поля в той или иной области пространства, достаточно проинтегрировать вектор Пойнтинга по объёму.
Волновое уравнение для электромагнитных волн
ротор (rot) и дивергенция (div) — это некоторые операции дифференцирования, производимые по определенным правилам над векторами.
Возьмем ротор от обеих частей уравнения
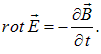
При этом воспользуемся доказываемой в курсе математики формулой:
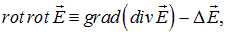
где 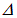 — введенный выше лапласиан. Первое слагаемое в правой части равно нулю в силу другого уравнения Максвелла:
— введенный выше лапласиан. Первое слагаемое в правой части равно нулю в силу другого уравнения Максвелла:
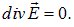
Получаем в итоге:
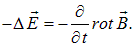
(2.93)
Выразим rotB через электрическое поле с помощью уравнения Максвелла:
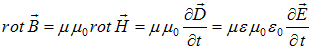
(2.94)
и используем это выражение в правой части (2.93). В результате приходим к уравнению:
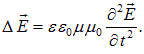
(2.95)
Учитывая связь
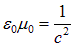
и вводя показатель преломления среды
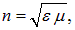
запишем уравнение для вектора напряженности электрического поля в виде:
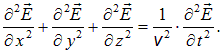
(2.96)
Сравнивая с (2.69), убеждаемся, что мы получили волновое уравнение, где v — фазовая скорость света в среде:
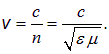
(2.97)
Взяв ротор от обеих частей уравнения Максвелла
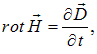
и действуя аналогичным образом, придем к волновому уравнению для магнитного поля:
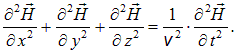
(2.98)
Полученные волновые уравнения для 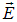 и
и 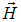 означают, что электромагнитное поле может существовать в виде электромагнитных волн, фазовая скорость которых равна
означают, что электромагнитное поле может существовать в виде электромагнитных волн, фазовая скорость которых равна
В отсутствие среды (при 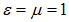 ) скорость электромагнитных волн совпадает со скоростью света в вакууме.
) скорость электромагнитных волн совпадает со скоростью света в вакууме.
Билет 12
Основу геометрической оптики образуют четыре закона: 1) закон прямолинейного распространения света; 2) закон независимости световых лучей; 3) закон отражения света; 4) закон преломления света.
Закон прямолинейного распространения света: свет в оптически однородной среде распространяется прямолинейно. Этот закон является приближенным, так как при прохождении света через очень малые отверстия наблюдаются отклонения от прямолинейности, тем большие, чем меньше отверстие.
Закон независимости световых пучков: эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены. Пересечения лучей не мешают каждому из них распространяться независимо друг от друга. Разбивая световой пучок на отдельные световые пучки, можно показать, что действие выделенных световых пучков независимо. Этот закон справедлив лишь при не слишком больших интенсивностях света. При интенсивностях, достигаемых с помощью лазеров, независимость световых лучей перестает соблюдаться.
Закон отражения: отраженный от границы раздела двух сред луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела в точке падения; угол отражения равен углу падения.
Закон преломления: луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред
sini1/sini2 = n12 = n2/ n1 , очевидно sini1/sini2 = V1/ V2, (1)
где n12 – относительный показатель преломления второй среды относительно первой. Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления n12 = n2/ n1.
Принцип суперпозиции (наложения) волн установлен на опыте. Он состоит в том, что в линейной среде волны от разных источников распространяются независимо, и накладываясь, не изменяют друг друга. Результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые частица получит, участвуя в каждом из слагаемых волновых процессов.
Согласно принципу суперпозиции накладываться друг на друга без взаимного искажения могут волны любой формы. В результате наложения волн результирующее колебание каждой частицы среды может происходить по любому сложному закону. Такое образование волн называется волновым пакетом. Скорость движения волнового пакета не совпадает со скоростью ни с одной из слагаемых волн. В этом случае говорят о скорости 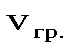 волнового пакета. Скорость перемещения максимума группы волн (волнового пакета)называется групповой скоростью. Она равна скорости переноса энергии волнового пакета.
волнового пакета. Скорость перемещения максимума группы волн (волнового пакета)называется групповой скоростью. Она равна скорости переноса энергии волнового пакета.
На практике мы всегда имеем дело с группой волн, так как синусоидальных волн, бесконечных в пространстве и во времени, не существует. Любая ограниченная во времени и пространстве синусоидальная волна есть волновой пакет (его называют цуг волны). Групповая скорость такого пакета совпадает с фазовой скоростью бесконечных синусоидальных волн, результатом сложения которых он является.
В общем виде связь между групповой и фазовой скоростями имеет вид:
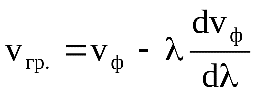 .
.
Принцип суперпозиции (наложения) волн заключается в следующем: в линейных средах волны распространяются независимо друг от друга, то есть волна не изменяет свойства среды, и другая волна распространяется так, будто первой волны нет. Это позволяет вычислять итоговую волну как сумму всех волн, распространяющихся в данной среде.
При сложении двух или более синусоидальных волн результирующая волна в общем случае уже не будет синусоидальной.
Рассмотрим в качестве примера результат сложения двух плоских однонаправленных волн с одинаковыми амплитудами и разными, но близкими частотами и волновыми числами:
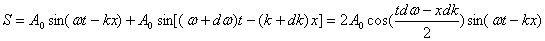
Полученная волна не является синусоидальной, так как величина перед синусом (амплитуда волны) меняется со временем и координатой. Однако, если на длине волны (и в течении периода) её изменения малы (что имеет место при малых dk и dw), волна ещё похожа на синусоиду; её иногда называют квазисинусоидальной. График этой волны представляет собой то, что мы в теории колебаний назвали биениями; однако здесь, в отличие от маятника, биения происходят не только во времени, но и в пространстве.
Условия возникновения интерференции:
Если на экран приемника попадают одновременно две произвольные электромагнитные волны Е1и Е2, то согласно принципу суперпозиции, напряженность результирующего поля равна Е= Е1+ Е2 Дляперехода к энергетическому описанию, возведем это равенство в квадрат
E2=(Е1+ Е2 )2=E12+E22+2E1E2,
Известно, что инерционность измерительной аппаратуры значительно превышает частоту колебаний оптического диапазона (
10
| |
| | 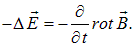 | (2.93) |
| | 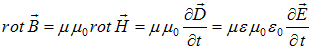 | (2.94) |
| | 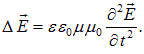 | (2.95) |
| | 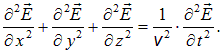 | (2.96) |
| | 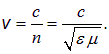 | (2.97) |
| | 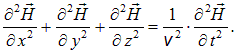 | (2.98) |
15 Гц). Воспользуемся понятием эргодичности, лежащим в основе метода вычисления наблюдаемых (средних) значений физических величин по тому или иному ансамблю Гиббса. Эргодическая гипотеза предполагает, что средние по времени значения физических величин, характеризующих систему, равны их средним статистическим значениям. Усредним по времени выражение и с данными опыта будем сравнивать значение среднего квадрата напряженности стационарного эргодического поля
В зависимости от того, что получается при усреднении произведения
<E1E2>, названного интерференционным членом, реализуются два случая:
1) если <E1E2>=0, то
2) если <E1E2>≠0, то I≠I1+I2,происходит перераспределение потока энергии в пространстве.
Неравенство
<E1E2>≠0 (1.15)
служит необходимым условием возникновения интерференции.
Когерентность (от латинского cohaerens – находящийся в связи) рассматривается как согласованное протекание во времени нескольких колебательных или волновых процессов, проявляющееся при их сложении. Колебания называют когерентными, если разность их фаз остается постоянной во времени и при сложении колебаний определяет амплитуду суммарного колебания. Два гармонических (синусоидальных) колебания одной частоты когерентны.
При сложении двух гармонических колебаний с одинаковой частотой, но с различными амплитудами A1 и A2 и фазами φ1 и φ2 образуется гармоническое колебание той же частоты ν:
п
а фазовый сдвиг
Амплитуда результирующих колебаний может изменяться от A1 + A2 до A1 - A2 в зависимости от разности фаз φ1 - φ1 .
Оптической длиной пути
Разность оптических длин путей называется оптической разностью хода волн
1 2 3
Условие минимумов и максимумов
Когда гребни волн на поверхности волны складываются в одной точке, их амплитуда резко возрастает. В этом случае говорят, что в этой точке образуется интерференционный максимум. Когда впадины волн на поверхности волны складываются в одной точке, их амплитуда резко уменьшается. В этом случае говорят, что в этой точке образуется интерференционный минимум. Интерференционные минимумы и максимумы образуются при соблюдении определенных условий.
Если разность хода волн равна нечетному числу полуволн, то в точке наложения этих волн образуется интерференционный минимум. Амплитуда колебаний в данной точке минимальна.
Δd=(2k+1)λ2
Время и длина когерентности.
Максимальная величина оптической разности хода двух волн, полученных делением одной волны на части, при которой еще наблюдается интерференция, называется длиной когерентности излучения. Длина когерентности излучения определяется длиной волны и шириной спектра излучения и равна
LK = λ2/ ∆λ
где ∆λ - ширина спектрального интервала в длинах волн, в пределах которого интенсивность излучения отлична от нуля.
Максимальное значение промежутка времени, при котором когерентность ещё сохраняется, называется временем когерентностиизлучения (tk).
Длина и время когерентности связаны следующим соотношением:
L K = t K V
где V- скорость света.
Способы наблюдения интерференции.
Для получения когерентных световых волн с помощью обычных (не
лазерных) источников света применяют метод разделения света от одного
источника на две или несколько систем световых лучей. Разделение одной и той же волны на две части для реализации
интерференции осуществляется двумя способами: 1) делением амплитуды; 2)
делением фронта волны
Метод Юнга.
Юнг в темной комнате пропустил солнечный свет через узкую щель, а
затем с помощью двух щелей, вырезанных в следующем экране, разделил
этот пучок на два. Эти два пучка, накладываясь друг на друга, образовали на
экране наблюдения систему полос - чередующихся максимумов и
минимумов интенсивности I.Таким образом, в опыте Юнга интерференционная картина получалась путем деления фронта волны, исходящей из одного источника, при ее прохождении через две близко расположенных щели. Этот опыт позволил
впервые определить длину световой волны. Простота и убедительность
опыта Юнга сделали его классическим, одним из самых ярких в истории
физики.
Бипризма Френеля. Существенные черты этого опыта сохраняются в
установке с бипризмой Френеля. Бипризма Френеля представляет собой две
прямоугольные призмы с малыми преломляющими углами β, сложенные
своими основаниям рактически она изготавливается из целого
куска стекла. Источником света является ярко освещенная узкая щель,
установленная параллельно ребру бипризмы. Можно показать, что,
поскольку угол β очень мал, все лучи при преломлении в бипризме
отклоняются на угол (n-1) β независимо от угла падения, если последний также мал. В результате за бипризмой лучи распространяются так, как если бы они
исходили из двух мнимых источников S1 и S2 (изображений входной щели). В
области пространства, где пучки от источников S1, S2 перекрываются,
возникает интерференционная картина. Расстояние между этими
источниками равно.
Опыт Ллойда
Устройство для наблюдения интерференции световых пучков. Свет от источника, расходящийся под небольшим углом, падает на отражающую поверхность, расположенную перпендикулярно экрану. Интерференционная картина наблюдается на экране в области перекрытия падающего и отраженного световых потоков. В опыте, предложенном Ллойдом, интерферируют лучи, исходящие непосредственно от источника S (рисунок) и отраженные от поверхности зеркала АВ. Лучи, отраженные от зеркала АВ, как бы исходят от мнимого источника S1 когерентного с S. Для того чтобы расстояние d между S и S' было достаточно мало, лучи должны отражаться от зеркала под углом, близким к 90°. Источником света служит щель, параллельная плоскости зеркала.
Особенность интерференционной картины, наблюдаемой с помощью зеркала Ллойда, заключается в том, что центральная полоса получается не светлой, а темной. Это указывает на то, что лучи, проходящие одинаковые геометрические пути, все же сходятся в опыте Ллойда с разностью хода λ/2. Такая «потеря» полуволны (или, другими словами, изменение фазы на π) происходит при отражении света от поверхности стекла, коэффициент преломления которого больше, чем воздуха. В дальнейшем мы увидим, в каких случаях при отражении света от прозрачной среды происходит потеря полуволны.
Интерференция при отражении от тонких пленок:
Интерференционная картина в отраженном свете возникает из-за наложения двух волн, отраженных от верхней и нижней поверхностей пленки. Рассмотрим сложение волн, выходящих из точки С. Плоскую волну можно представить как пучок параллельных лучей. Один из лучей пучка (2) непосредственно попадает в точку С и отражается (2')в ней наверх под углом, равным углу падения
Оптическая разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке С, равна
| | |
Просветление оптики
Просветление оптики - нанесение на поверхность линз, граничащих с воздухом, тончайшей плёнки или нескольких плёнок одна поверх другой. Это необходимо для увеличения светопропускания оптической системы. Показатель преломления таких плёнок меньше показателя преломления стёкол линз. Просветляющие плёнки уменьшают светорассеяние и отражение падающего света от поверхности оптического элемента, соответственно улучшая светопропускание системы и контраст оптического изображения. Просветлённый объектив требует бережного обращения, так как плёнки, нанесенные на поверхность линз, легко повредить. Кроме того, тончайшие пленки загрязнений (жир, масло) на поверхности просветляющего покрытия нарушают его работу и резко увеличивают отражение света от загрязненной поверхности. Следует помнить, что следы пальцев со временем разрушают не только просветление, но и поверхность самого стекла. По методике нанесения и составу просветляющего покрытия просветление бывает физическим (напыление) и химическим (травление).