Однослойное просветление

Отражательная способность стекла, просветленного таким способом, сильно зависит от длины волны, что является основным недостатком однослойного просветления. Минимум отражательной способности соответствует длине волны λ=4d·n, где d — толщина пленки, n — ее показатель преломления

В настоящее время однослойное просветление часто используется для лазерной оптики, рассчитанной на работу в узком спектральном диапазоне. Используя стекла с относительно высоким показателем преломления и напыляя пленку фторида бария, удается добиться минимальной отражающей способности около 1 %. Главным преимуществом такого просветления является его дешевизна.

Многослойное просветление

Многослойное просветляющее покрытие представляет собой последовательность чередующихся слоев (их число достигает 15 и более) из двух (или более) материалов с различными показателями преломления. Многослойные просветляющие покрытия характеризуются низкими потерями на отражение (узкополосные покрытия для лазерной оптики с отражательной способностью около 0,3 % и менее, широкополосные — до 0,5 %). Основное преимущество многослойного просветления применительно к фотографической и наблюдательной оптике — незначительная зависимость отражательной способности от длины волны в пределах видимого спектра (на графике отражательной способности от длины волны наблюдаются два и более минимума, разделенных небольшими максимумами, а за пределами рабочей полосы наблюдается сильный рост отражательной способности), что существенно уменьшает искажения цвета

Билет 13
Принцип Гюйгенса–Френеля

формулируется следующим образом: каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Другими словами, принцип Гюйгенса-Френеля описывает, как волна распространяется через среду. Он гласит, что каждая точка, достигнутая волной, может рассматриваться как источник новой сферической волны с частотой, равной частоте падающей волны.

Принцип Гюйгенса – Френеля позволяет наглядно и геометрически объяснить такие явления, как отражение.
Метод зон Френеля

кольцевые участки, на которые разбивают сферическую поверхность фронта световой волны при рассмотрении задач о дифракции волн в соответствии с принципом Гюйгенса – Френеля для упрощения вычислений при определении амплитуды волны в заданной точке пространства. Пусть монохроматическая волна распространяется из точки

---

в точку наблюдения . Положение волнового фронта в определенный момент времени указано на рисунке. Согласно принципу Гюйгенса – Френеля действие источника заменяют действием вторичных (воображаемых) источников, расположенных на поверхности фронта сферической волны, которую разбивают на кольцевые зоны так, чтобы расстояния от краёв соседних зон до точки наблюдения отличались на где – длина волны. (На рисунке – точка пересечения фронта волны с линией , расстояние = , = ). Тогда расстояние от края -й зоны до точки наблюдения равно

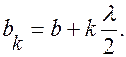(6.37.22)

Внешний радиус -й зоны Френеля

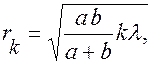(6.37.23)

площадь -й зоны

---

(6.37.24)

при не слишком больших площади зон Френеля одинаковы.

Дифракция Френеля и дифракция Фраунгофера

Распределение амплитуды волны в плоскости наблюдения зависит от размеров и формы препятствия, на котором происходит дифракция. Аналитический расчет дифракционной картины в общем случае представляет сложную математическую задачу. Сложность решения задачи дифракции волн во многом зависит от числа зон Френеля, укладывающихся на препятствии, и в зависимости от этого различают дифракцию Фраунгофера и дифракцию Френеля.

Дифракция Фраунгофера имеет место, если размеры препятствия много меньше радиуса первой зоны Френеля как со стороны источника, так и со стороны плоскости наблюдения, т. е.

 

и .

Это будет в том случае, если источник и точка наблюдения находятся достаточно далеко от препятствия, на котором происходит дифракция. При большом удалении источника можно считать, что приходящая от него волна является плоской. Таким же образом вторичные сферические волны, приходящие в удаленную точку наблюдения, можно считать плоскими. Поэтому говорят, что дифракция Фраунгофера наблюдается в параллельных пучках или в дальней зоне.
Зоны Френеля

это цилиндрический эллипс, проведенный между передатчиком и приемником. Размер эллипса определяется частотой работы и расстоянием между двумя участками. Когда радиосигнал проходит между передатчиком и приемником, он может распространяться несколькими путями. Он может идти напрямую между передатчиком и приемником (основной сигнал). Сигнал может отражаться от земли и затем переноситься на удаленный приемник (отраженный сигнал). Он может идти влево или вправо и отражаться от "холма" (еще один отраженный сигнал).

По сути, внутри этого эллипса располагается вся полезная энергия и передаваемая информация. Для того, чтобы сигнал мог быть эффективно передан, должны соблюдаться два условия:

• 
  обеспечена прямая видимость между передатчиком и приемником;
  
• 
  не менее 60% занимаемого эллипса должно быть свободно от препятствий. 
  

---

Для расчета радиуса зоны Френеля можно воспользоваться упрощенной, но подтвержденной на практике формулой:



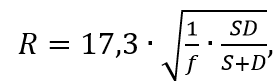
где R – радиус зоны Френеля (м);
S,D – расстояние от антенн до самой высокой точки предполагаемого препятствия (км);
f – частота (ГГц).

Дифракция Френеля от круглого отверстия и диска

Схожие дифракционные явления можно наблюдать при прохождении света через малое отверстие или, как принято говорить, от дополнительного экрана — диска, размером в это отверстие. Пусть плоская световая волна падает на малое круглое отверстие радиусом а

Плоский фронт, совпадающий с отверстием, можно рассматривать как совокупность фиктивных источников, испускающих когерентные волны, которые в точке наблюдения Р будут интерферировать. Разобьем площадь отверстия на ряд кольцевых зон Френеля, для чего из точки Р проведем ряд сфер с радиусами:



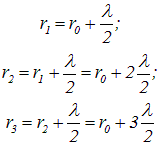
и т. д.

Если число зон, которые укладываются в отверстии, четно, то в точке Р будет темное пятно. Действительно, результирующая амплитуда колебаний при 2-х, 4-х, ... 2m зонах равна соответственно

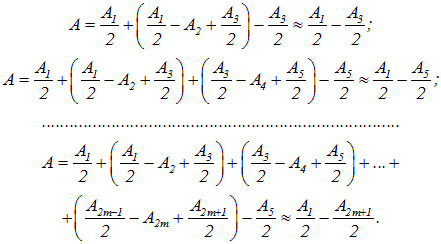(5.13)

При небольших отверстиях (небольших m) амплитуды А₁ и А_m2+1 мало отличаются друг от друга, поэтому результирующая амплитуда будет мала, и в точке наблюдения будет темное пятно.

При нечетном числе зон k = 2m-1 (m=1, 2, 3, ...) аналогичные рассуждения приводят к выражению

(5.14)

то есть в точке наблюдения будет светлое пятно.

число зон Френеля, укладывающихся в отверстии, зависит от расстояния  и длины волны

---

:

(5.15)

откуда число открытых зон получается равным

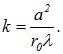(5.16)

Таким образом, при данном радиусе отверстия а и длине волны падающего света число зон Френеля к является функцией расстояния  между отверстием и точкой наблюдения.

Дифракция Фраунгофера от щели

Дифракция Фраунгофера наблюдается, когда источник света сильно удален от места наблюдения, в результате фронт волны можно считать плоским.

разность хода двух волн от краев щели равна Δ = b sin φ.

Разобьем MN на отрезки длиной λ/2. Параллельно произвольному направлению луча через точки разбиения (1, 2, 3) проведем линии, которые разделят открытую часть волновой поверхности MN на участки равной ширины – зоны Френеля, параллельные краям щели. По построению ∆ – разность хода лучей от краев зон Френеля равна λ/2. Это означает, что волны, идущие от двух соседних зон при наложении погасят друг друга. Т.о., если на открытой части волновой поверхности для данного направления наблюдения уложится целое четное число зон Френеля, то для данного направления будет наблюдаться min интенсивности, т.к. зоны попарно друг друга погасят.

Четное число зон Френеля - минимум дифракции



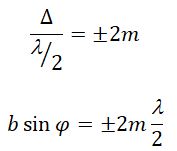
m = 1, 2, 3...

Если число зон Френеля целое и нечетное, то в этом направлении будет наблюдаться max:



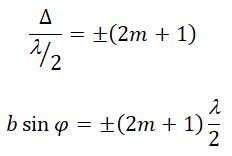
m = 0, 1, 2, 3...

Дифракционная решетка

оптическое устройство, представляющее собой совокупность большого числа параллельных, обычно равноотстоящих друг от друга, щелей.

Дифракционную решетку можно получить нанесением непрозрачных царапин (штрихов) на стеклянную пластину. Непроцарапанные места — щели — будут пропускать свет; штрихи, соответствующие промежутку между щелями, рассеивают и не пропускают света. Сечение такой дифракционной решетки (

---

Смотрите также файлы

• Ортаы топ аралы диагностиканы нтижелерін баылау параы Оу жылы 20212022оу жылы Топ Ботаан ткізу мерзімі 0110. 01. 2022ж.docx

• Отчет по дисциплине Тестирование и отладка программного обеспечения Лабораторная работа 3 по теме Тестирование по стратегии белого ящика.docx

• Задание Заполните таблицу Культура молодёжного бунта Название молодёжной субкультуры.docx

• Задача 137 Заряд равномерно распределен по всему объему однородного сферического диэлектрика ( 3 ) радиусом r 5,0 см.doc

• Разночинец, рантье, метис, горожанин, пенсионер, ребенок.docx