- уменьшение числа в несколько раз (прямая и косвенная форма): В первый день турист прошел 20 км, а во второй день – в 2 раза меньше. Сколько километров прошел турист во второй день? (прямая форма); Один метр шелка стоит 90 рублей, в 3 раза дороже, чем один метр ситца. Сколько стоит один метр ситца? (косвенная форма).

Это основные виды простых задач, они не исчерпывают всего многообразия задач.

Задание 5. Выберите из учебника математики 1 класса задания (не менее 6 заданий), подготавливающие младших школьников к введению понятия «арифметическая задача». Разработайте два задания.

Задание 6. Прочитайте задачу:«В школьную столовую привезли 6 кг лимонов, яблок на 24 кг больше, чем лимонов, а груш на 12 кг меньше, чем яблок. Сколько килограммов груш привезли в школьную столовую?»

Вопросы:

¾    Каким способом (синтетическим, аналитическим или аналитико-синтетическим) лучше проводить разбор этой задачи?

аналитико-синтетическим

¾    Покажите методику работы над арифметической задачей на примере данной задачи (этапы работы над задачей смотрите в лекции).

 1. Работа над содержанием задачи. Анализ условия. Выразительно прочитать условие задачи. О чем говорится в задаче? (о весе фруктов, привезенных в столовую) Сколько весовых величин выделили в задаче? (лимоны, яблоки, груши). Как вес каждого сорта фруктов различен между собой? (6 кг лимонов, яблок на 24 кг больше, чем лимонов, а груш на 12 кг меньше, чем яблок).

2. Поиск решения задачи. Составим наглядную таблицу условия задачи

лимоны	6 кг
яблоки	Больше на 24 кг, чем лимоны
Груши- ?	Меньше на 12 кг, чем яблоки

Рассуждаем, рассматривая табличное условие задачи, выведенное на доску. Как узнать сколько весят груши, если их вес меньше на 12 кг, чем яблоки? (Вычесть из веса яблок 12 кг). Но нам не известен вес яблок, но мы знаем по условию задачи, что их вес больше на 24 кг, чем лимонов. Как узнаем их вес? (К весу лимонов прибавим 24 кг). По условию задачи вес лимонов известен, поэтому данное действием будет первым в решении задачи.

3. Решение задачи.

Итак, совершив поиск решения задачи, разделив ее на 2 простых действия получим:

1. 24+6= 30 (кг)- вес яблок

---

2. 30-12= 18 (кг)- вес груш

4. Формулируем ответ к задаче (18 кг груш привезли в столовую)

5. Делаем проверку решения задачи

Задания по теме 5.4 Доли и дроби, элементы стохастики в современном начальном математическом образовании 

Цель: формирование умений осуществлять диагностику и оценку учебных достижений учащихся; умений проектировать учебную деятельность на уроке с учетом поставленных целей и задач.

Задание 7.  Разработайте контрольно-измерительные материалы для диагностики результатов обучения младших школьников по теме «Дроби». Вид контрольно-измерительных материалов по выбору. В работе должно быть не менее 10 заданий.

 1.Запишите под картинкой, где возможно, соответствующие рисункам дроби.



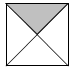
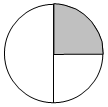
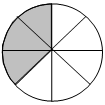
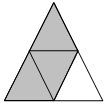
2. Запишите дроби, у которых:

числитель 5, знаменатель 8;

знаменатель 4, числитель 1;

знаменатель 7, числитель 11;

числитель 7, знаменатель 12.

3. Запишите цифрами дроби:

семь тринадцатых;

восемь одиннадцатых;

шесть девятых;

девять десятых;

двадцать шестых.

4. Сравните дроби и поставьте знаки сравнения.

4/5 … 3/5 5/6...1/6 3/8...7/8

5. Токарь выточил на токарном станке 100 деталей, что составляет 4/5 дневной нормы. Какова его дневная норма?

6. В аквариуме 12 рыбок. 5 из них зеленого цвета, 3 красного и 2 синего. Какую часть составляют рыбки зеленого цвета? Какую часть составляют рыбки красного цвета? Какую - синего?

7. Двенадцатая часть года – это:
а) 1 месяц б) 1 неделя в) 1 сутки

8. Закрась указанную часть фигуры.



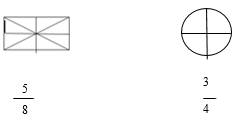
9. Путник прошел шестую часть пути и понял, что ему осталось пройти 10 км. Какова длина всего пути?

10. В книге 63 страницы. Аня прочитала 3/7 книги. Сколько страниц осталось прочитать девочке?

Задание 8. Изучите конспект урока.

 

Урок математики в 4 классе по теме «Доли и дроби».

---

Цель урока: дать общее представление о долях, научить учащихся называть, записывать и сравнивать доли

Задачи урока:

- обучающие – ввести новое понятие «доля числа», учить определять долю числа, записывать дроби, познакомить с терминами «доля», «дробь», «числитель», «знаменатель»;

- развивающие – развивать логическое мышление, математическую речь, навыки устного счета, внимание, память, мышление;

- воспитывающие – воспитывать коллективизм, аккуратность.

Ход урока

1. Знакомство с темой урока.

– Людям часто приходится делить целое на доли. А помните известный мультик «Апельсин» Посмотрим, как животные делили апельсин. Смотрите внимательно, после просмотра я задам вам вопросы.

- Как в песенке, животные называют равные части? (Дольки).

– Кто из вас был внимательным? Сколько долек было в апельсине? (Пять долек).

– Сколько долек поучил каждый? (Одну дольку апельсина).

- Как вы думаете, апельсин был разделён на равные части? (Да).

- Как по-другому, можно назвать эти равные части? (Доли).

2. Постановка учебных задач.

- Как на языке математики назвать и записать, какую долю (часть) апельсина получил каждый из животных? ( Не знаем)

- Что, на ваш взгляд, нам следует узнать, чему научиться? (Научиться записывать, называть и сравнивать доли).

- В результате совместных рассуждений, мы определили цель урока. (Научиться записывать, называть и сравнивать доли).

3. Работа над формированием понятий «Доли» и «Дроби».

- Давайте, определим, что же называют долями? Для этого еще раз вспомним, как животные делили апельсин

- Сколько частей досталось каждому животному? ( По одной части).

- Что можно сказать про каждую из частей? Какие это части? (Равные).

- Значит, каждому досталось по одной равной части от целого апельсина.

- Сделайте вывод, что такое доля. (Доля – это одна или несколько равных частей целого.)

(На доске появляется запись: 1 часть из 5).

В математике пишут короче: 1/5. Для записи понадобится 2 клеточки, между ними проводим черту. Число под чертой показывает, на сколько равных частей мы разделили предмет, а над чертой – сколько таких частей взяли. Читаем запись, запишите.

- Когда мы «делим» натуральные числа, то используем знак (:).

- Но в математике есть еще один знак деления, он называется, «дробная черта» - соответственно числа, записанные с этим знаком, называются дробными.

- Кто догадался, как называется данная запись? (Дробь).

- Верхняя часть дроби называется числителем, а нижняя – знаменателем.

---

- Что обозначает знаменатель в записи дроби? (На сколько частей разделили предмет).

- Что обозначает числитель? (Сколько частей взяли).

4. Отработка умения находить часть от целого и обозначать её дробью. Сравнение дробей.

Вопросы:

¾    Разработайте задания для 4 этапа урока (работа с количеством заданий – не менее 6 заданий).

¾    Какие вопросы можно предложить учащимся на этапе рефлексии?

 4. Отработка умения находить часть от целого и обозначать её дробью. (Цель этапа - обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы. УУД - познавательные: построение логической цепи рассуждений; самостоятельное создание способов решения проблем поискового характера; коммуникативные: инициативное сотрудничество в поиске и сборе информации со сверстниками и с учителем).

Практическая работа.

-Возьмите полоску бумаги длиной 6 см и согните её пополам. Сколько равных частей получилось? (Две равных части).

- Верно. Каждая часть – это половина полоски или одна вторая часть полоски.

-А как получили1/2 часть полоски? (Согнули полоску пополам и взяли только одну часть).

-Закрасьте одну такую долю полоски.

- Кто догадался, как можно найти длину половины полоски? (Измерить линейкой.

6 : 2 = 3 см).

Запись в тетради.

-Возьмите полоску длиной 8 см и разделите её на 4 равные части. Чтобы разделить на 4 равные части, надо знать длину 1/4 части. Как узнать длину 1/4части? ( 8 : 4 = 2 см)

- Правильно. Разделите по линейке полоску, согните и покажите мне 1/4 часть.

Запись в тетради.

- Прочитаем следующее задание.

– Какую фигуру надо начертить? (Квадрат ).

– Чему равна сторона квадрата?

- Начерти в тетради квадрат, длина стороны которого 3см. Раздели его на равные части так, чтобы можно было закрасить одну вторую его часть, одну четвёртую.

- Почему именно равных?

- Нужна доля, значит, части должны быть равными.

- На сколько частей будем делить, чтобы получить 1/16? (На 16 частей.)

- Сколько клеточек будет в одной шестнадцатой доле? Какой формы будет эта доля?

(Квадрат).

- Раскрасьте ее, подпишите внизу эту долю.

- А теперь проверим вашу сообразительность. Сыр нужно разделить на 8 частей, сделав только 3 разреза. Попробуйте решить ее, можете посовещаться с соседом. Подготовьтесь для объяснения. После выступления детей с вариантами решения- проверка.- Какая часть сыра осталась на блюде? (половина, 1/2, 4/8)

---

Здесь учитель может подвести детей к тому, что можно брать несколько долей, если осталось 4 части из 8, то это 4/8, значит 4/8 и 1/2это равные доли. Пропедевтика изучения обыкновенных дробей.
Итог урока. Рефлексия. (Цель этапа - оценить работу каждого учащегося. УУД - познавательные: умение структурировать знания; коммуникативные: аргументировать свои высказывания; регулятивные: саморегуляция, самооценка).

Обобщение полученных на уроке сведений. Заключительная беседа. Выставление оценок.

- Чему научились на уроке? Что такое доли? Что называют дробями?

- Какой материал повторили?

- Где и когда вы можете применить свои знания на практике?

- У кого не было затруднений в новой теме? В решении задач?

- Как оцениваете свою деятельность на уроке?

Задания по теме 5.5 Обучение элементам алгебры в начальной школе

Цель: формирование умений проектировать учебную деятельность с учетом возраста и индивидуальных особенностей обучающихся; умений находить и использовать методическую литературу и другие источник информации, необходимые для подготовки к урокам.

          Задание 9. Разработайте дифференцированные задания для самостоятельной работы (высокого, среднего, низкого уровня сложности) для учащихся начальной школы по проверке умений и навыков решать уравнения различного вида (не менее 5 заданий по 3 уровня сложности в каждом задании)

1 задание:

1 уровень - Реши уравнение: х +5= 15

2 уровень – Найди уравнение, которое составлено неправильно. Исправь его и реши.

73 – х = 40

50 – х = 64

х + 25 =50

3 уровень- Найди уравнение, которое решается сложением, и реши его.

72 – х = 40

х + 35 =60

х -24 = 46

25 : х = 5

9 + х = 59

2 задание.

1 уровень

Выбери правильное утверждение и подчеркни его.

1. 
   Уравнение – это пример, в котором пропущено число.
   
2. 
   Уравнение – это выражение с неизвестным компонентом.
   
3. 
   Уравнение – это равенство, содержащее неизвестную величину.
   

Среди данных выражений подчеркни уравнения.

Х+8=17 2+а+5 (с-8)*3

10-р=5 5-3-2 5+3
2 уровень

Закончи решения уравнений

х+8=17 с-20=40 58-е=8

х=17… с=… е=…

х=… с=…

…+8=17 …-20=40

…=17 …=40

3 уровень

Реши уравнения.

42:х=21 х:8=7 15*х=45


3 задание.

1 уровень.

Реши уравнения, пользуясь памяткой: «Чтобы найти целое надо сложить части. Чтобы найти часть надо из целого вычесть известную часть»

---

Смотрите также файлы

• Выполнение практических заданий по дисциплине управленческий консалтинг.docx

• Образования Российской Федерации.docx

• Особенности восприятия обществоведческого материала младшими школьниками. Условия усвоения исторического материала учащимися 34кл.pptx

• К какому классу относятся опасные условия труда.docx

• Дисциплина Педагогика Практическое занятие 1 Обучающийся Лисун Людмила Леонидовна Преподаватель Степанова Елена Ивановна Задания по теме 1 Профессиональная яконцепция педагога.rtf