Файл: Ткачева М. В, Федорова Н. Е. и др., под ред. Жижченко А. Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 55
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Производная второго порядка (вторая производная). Производная второго порядка есть первая производная от производной первого порядка.
Производную определяют, как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к 0, если такой предел существует.
Точка максимума функции. Точку х0 называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство
Точка минимума функции. Точку х0называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство
Точка перегиба. Точки, в которых выпуклость вверх меняется на выпуклость вниз или наоборот, называются точками перегиба.
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y=f(x) убывает на интервале X, если для любых х1 и х2,
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка.
Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка.
Алгоритм нахождения интервалов выпуклости графика функции:
-
Найти область определения функции -
Найти вторую производную функции -
Найти точки, в которых вторая производная равна нулю или не существует -
Найти интервалы, на которые область определения функции разбивается этими точками -
Определить знаки второй производной на каждом интервале -
Если f '‘(х) < 0, то кривая выпукла вверх;
если f '‘(х) > 0 то кривая выпукла вниз.
-
Точки, в которых вторая производная меняет знак, - точки перегиба.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.Найти интервалы выпуклости и точки перегиба функции
Решение:
-
Область определения данной функции D(y) = (-∞; +∞) -
Найдем вторую производную функции: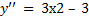
-
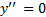 при х = 1, х = -1
при х = 1, х = -1 -
Определим знаки второй производной на каждом интервале (-∞; -1), (-1; 1), (1; +∞), используя метод интервалов (рис. 1).

Рисунок 1 – интервалы на числовой прямой
-
Так как на интервалах (-∞; -1) и (1; +∞) вторая производная положительна, то на этих интервалах функция выпукла вниз.
Так как на интервале (-1; 1) вторая производная отрицательна, то на этом интервале функция выпукла вверх.
Так как при переходе через точки х = 1 и х = -1 вторая производная меняет знак, то эти точки являются точками перегиба.
Ответ: функция выпукла вниз на интервалах (-∞; -1), (1; +∞);
функция выпукла вверх на интервале (-1; 1);
х = 1, х = -1 – точки перегиба.
Пример 2.Найти точки перегиба функции у=sinх
Решение:
Найдем вторую производную заданной функции
У'=соsх
У"= -sinх
Приравняем её к нулю и найдем корни полученного уравнения -sinх=0
В промежутках
Функция у=sinх принимает положительные значения, следовательно, У"= -sinх <0, а в промежутках
У" >0. Значит, в точках
Ответ:
Пример 3.Точка движется по закону S(t) = 3t4 – 8t3 + 2t – 3. В какой момент времени ускорение точки будет равно 48?
Решение:
Ускорение - это вторая производная s(t).
Найдем уравнение ускорения.
v=S'(t) = 12t3 – 24t2 + 2
a= S''(t) = 36t2 – 48t
Остается подставить вместо ускорения его значение равное 48 и решить уравнение.
36t2 – 48t=48
36t2 – 48t-48=0
При решении один корень получается отрицательный, чего не может быть по условиям задачи, а второй корень равен 2
Ответ: 2
Пример 4. Найдите интервалы выпуклости вверх и выпуклости вниз и точки перегиба функции f(x) = x3 – 6xlnx.
Проверьте свое решение.
Решение:
-
D(f) = (0; +∞) -
f (x) = (x3 – 6xln x)
(x) = (x3 – 6xln x)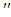
-
f (x) = 0 при х = 1, х = -1.
(x) = 0 при х = 1, х = -1.
f
С учетом области определения функции, х = 1
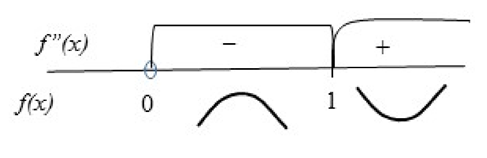
-
Так как на интервале (1; +∞) вторая производная положительна, то на этом интервале функция выпукла вниз.
Так как на интервале (0; 1) вторая производная отрицательна, то на этом интервале функция выпукла вверх.
Так как при переходе через точку х = 1 вторая производная меняет знак, то эта точка является точкой перегиба.
Ответ: функция выпукла вниз на интервале (1; +∞);
функция выпукла вверх на интервале (-1; 1);
х = 1– точка перегиба.
Р
 ассмотримфункция
ассмотримфункция Определение 1.
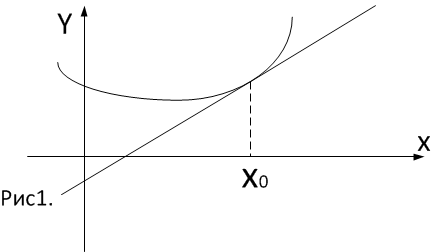
Если в дельта окрестности точки
Если в дельта окрестности точки
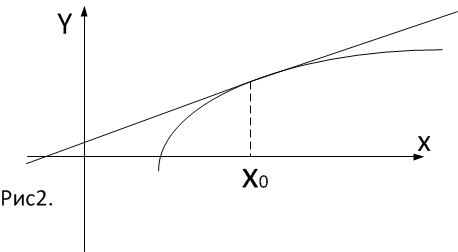
Е
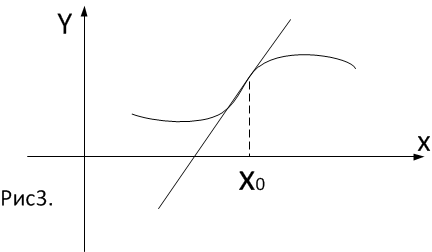 сли в дельта окрестности точки
сли в дельта окрестности точки Кроме этого, введем в рассмотрение понятие о выпуклости и вогнутости функции на интервале
Возьмём точки
, очевидно,
Определение 2.
Е
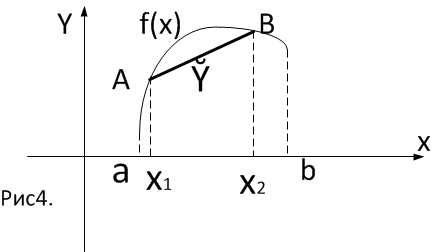 сли
сли ( выпукла вверх).
Е
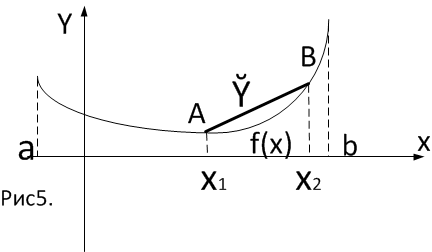 сли
сли ( выпукла вниз).
Вернемся к рассмотрению функции
Если в дельта окрестности точки
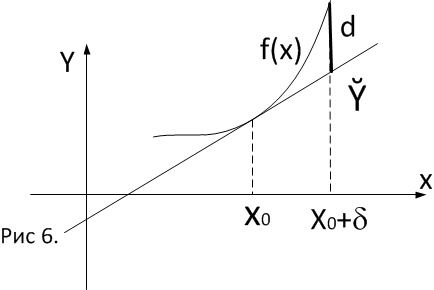
то функция
если в дельта окрестности точки