то функция   в точке   выпукла,

если в окрестности точки   меняет знак при переходе через точку   , то это точка перегиба.

Теорема 1.(достаточное условие выпуклости и вогнутости функции)Если функция   определена, непрерывна и дважды дифференцируема на интервале   и

1.   функция на интервале   вогнута

2.   функция на интервале   выпукла.

Доказательство: Возьмём для   и проведем в этой точке касательную к графику функции 

Кроме того, в окрестности точки   функция   представима по формуле Тейлора (с остаточным членом в форме Лагранжа) в виде



где 

тогда разность между ординатами кривой и касательной к графику функции в точке 

---

 будет равна







Знак   совпадает со знаком  . Для значений  , близких к  , в силу непрерывности функция   имеет тот же знак, что и   .

Если   то и   и функция в точке   вогнута, в силу произвольности точки   и на интервале  .

Если   то и   и функция в точке   выпукла, в силу произвольности точки   и на интервале   

---

Теорема 2.(необходимое условие точки перегиба)

Если функция   непрерывная с непрерывной производной до второго порядка включительно, имеет в точке   точку перегиба, то



Доказательство: следует из теоремы 1.

Теорема 3.(достаточное условие точки перегиба)

Если функция   непрерывная с непрерывной производной до второго порядка включительно, и вторая производная функции   при переходе через точку   меняет знак , то точка   точка перегиба.

Доказательство: следует из теоремы 1.

Пример 1. Исследовать функцию     и построить схематический график.

1 шаг: находим производную функции   

находим стационарные точки функции 



точек, в которых  точек, в которых производная не существует, тоже нет.

таким образом, все критические точки нашей функции 

---

2 шаг+3 шаг: отмечаем на оси   все критические точки функции   и составляем схему изменения знака производной функции   в интервалах между критическими точками функции + на основании схемы делаем вывод о интервалах убывания или возрастания функции.





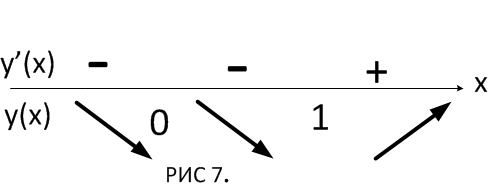
4 шаг: на основании схемы делаем вывод о характере критических точек.



5 шаг: находим вторую производную функции  и точки, к которых вторая производная функции   или  отмечаем на оси   все точки функции, в которых  или   и составляем схему изменения знака второй производной функции   в интервалах между отмеченными точками, на основании схемы делаем вывод о интервалах вогнутости или выпуклости функции.

находим производную функции   

находим точки, в которых вторая производная функции 

---

точек, в которых 

Вторая производная функции   меняет знак при переходе через точки  ,



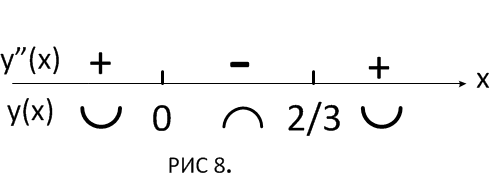
График функции имеет вид:







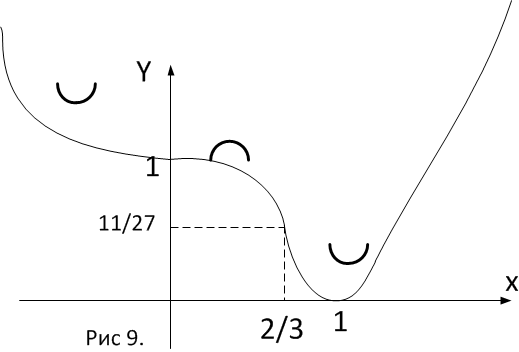
Исследование стационарных точек

с помощью производных высших порядков

Теорема 4 (достаточное условие экстремума)

Если функция   в стационарной точке x₀ имеет конечную производную второго порядка и

если  , то точка x₀ – точка максимума функции  ,

если  , точка x₀ – точка минимума функции

Теорема 5 (II достаточное условие точки перегиба)

Если функция

---

Смотрите также файлы

• 1. Теоретические аспекты темы.docx

• Сохранение психологического здоровьявоспитанников.pdf

• Определение величины транспортных запасов материальнотехнических ресурсов.docx

• Рабочая программа Занимательный русский язык.docx

• Понятие дееспособности.docx