Файл: Ткачева М. В, Федорова Н. Е. и др., под ред. Жижченко А. Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 56
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
имеет в точке x0
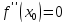 ,
, 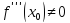 , то x0 – точка перегиба функции
, то x0 – точка перегиба функции  .
.
Теорема 6 (III достаточное условие экстремума)
Если число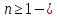 нечетно и функция
нечетно и функция  имеет производные до
имеет производные до 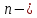 го порядка включительно в окрестности точки
го порядка включительно в окрестности точки  и производную
и производную 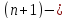 го порядка в точке
го порядка в точке  и
и 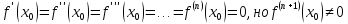 , то
, то
если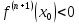 , то точка x0 – точка максимума функции
, то точка x0 – точка максимума функции  ,
,
если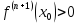 , точка x0 – точка минимума функции
, точка x0 – точка минимума функции 
Теорема 7 (III достаточное условие точки перегиба)
Если число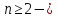 четно и функция
четно и функция  имеет производные до
имеет производные до 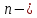 го порядка включительно в окрестности точки
го порядка включительно в окрестности точки
 и производную
и производную  го порядка в точке
го порядка в точке  и
и  , то
, то
x0 – точка перегиба графика функции .
.
Пример 2. Исследовать функцию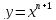
 и построить схематический график.
и построить схематический график.
Если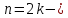 четно, то в точке
четно, то в точке  имеем
имеем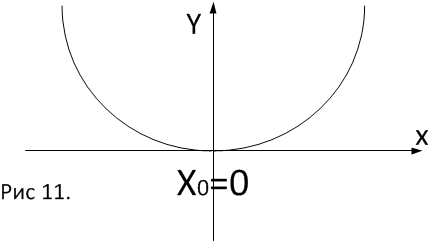
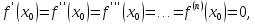
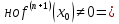
x0 – точка перегиба графика функции
Если число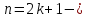 нечетно,
нечетно,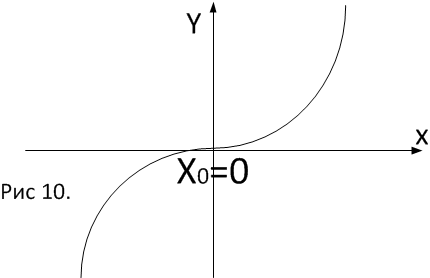
то в точке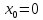 имеем
имеем
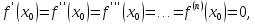
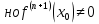
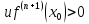 ,
,
то точка x0 – точка минимума функции
Теорема 6 (III достаточное условие экстремума)
Если число
если
если
Теорема 7 (III достаточное условие точки перегиба)
Если число
x0 – точка перегиба графика функции
Пример 2. Исследовать функцию
Если

x0 – точка перегиба графика функции
Если число

то в точке
то точка x0 – точка минимума функции