Файл: Контрольная работа 3 Вариант 1 Вычислить пределы, не используя правило Лопиталя 1 2.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 47
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
;
2.3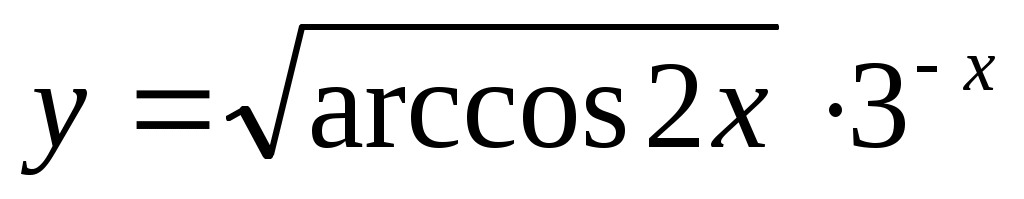 .
.
3.1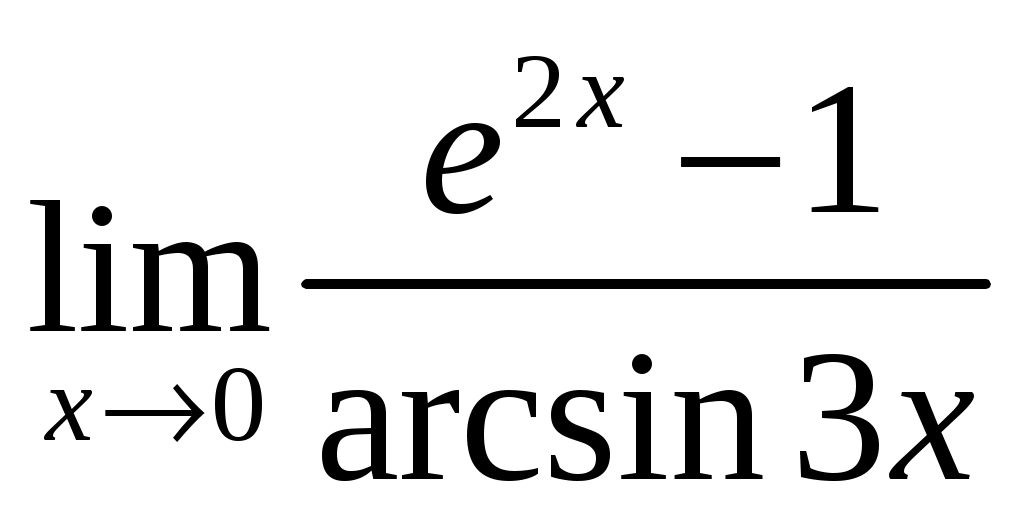 ; 3.2
; 3.2 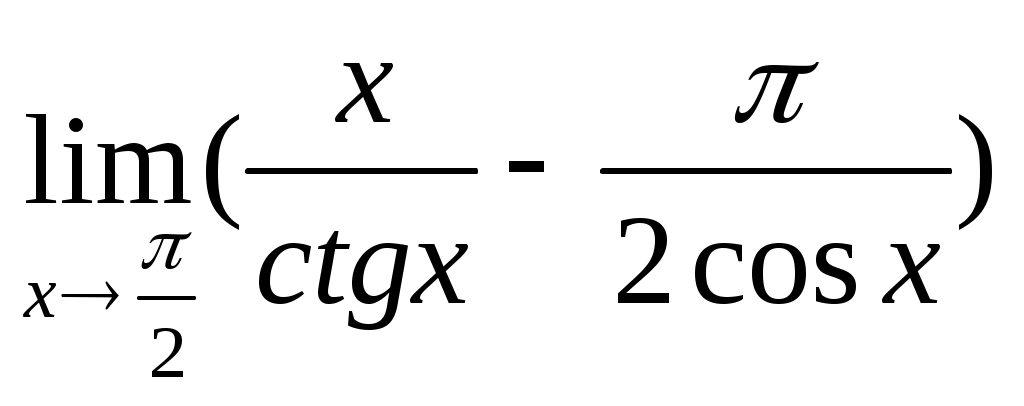 .
.
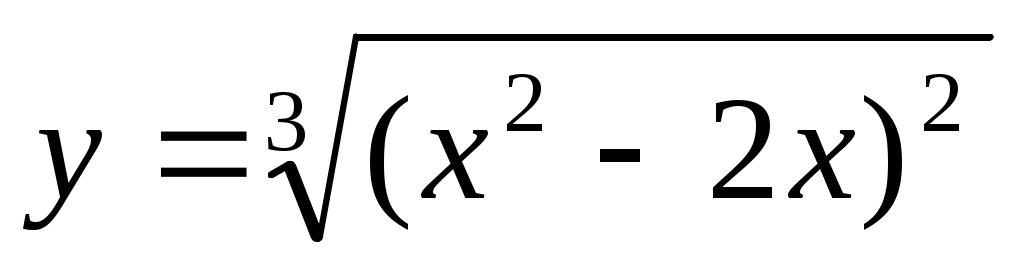 на отрезке [-1, 3].
на отрезке [-1, 3].
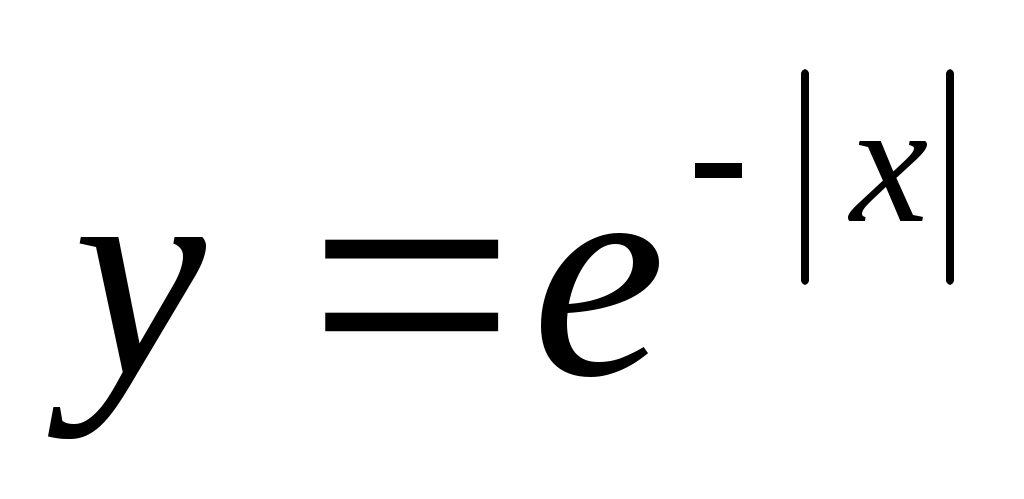 .
.
Вариант № 15
1.1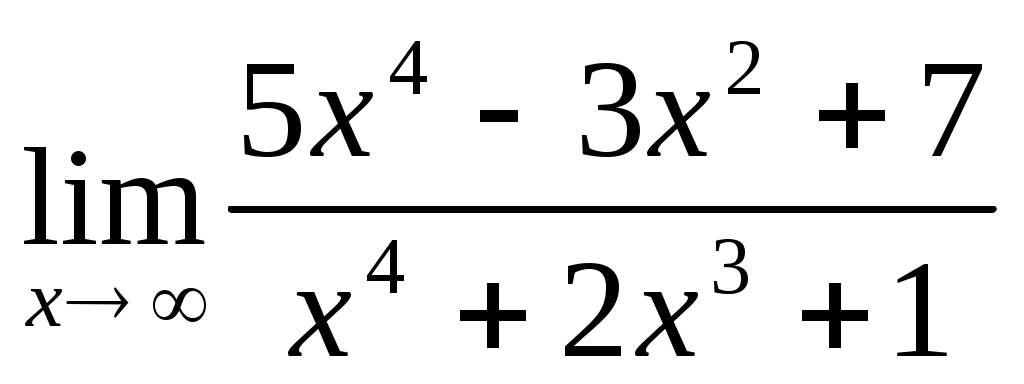 ; 1.2
; 1.2 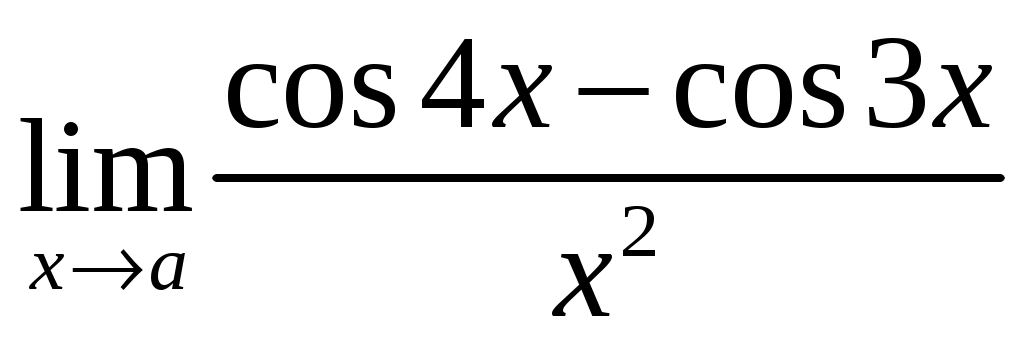 ;
;
1.3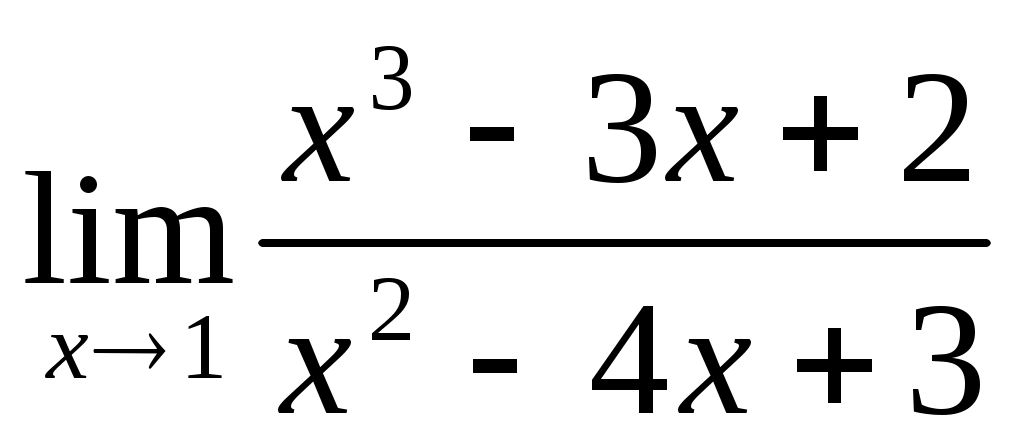 ; 1.4
; 1.4 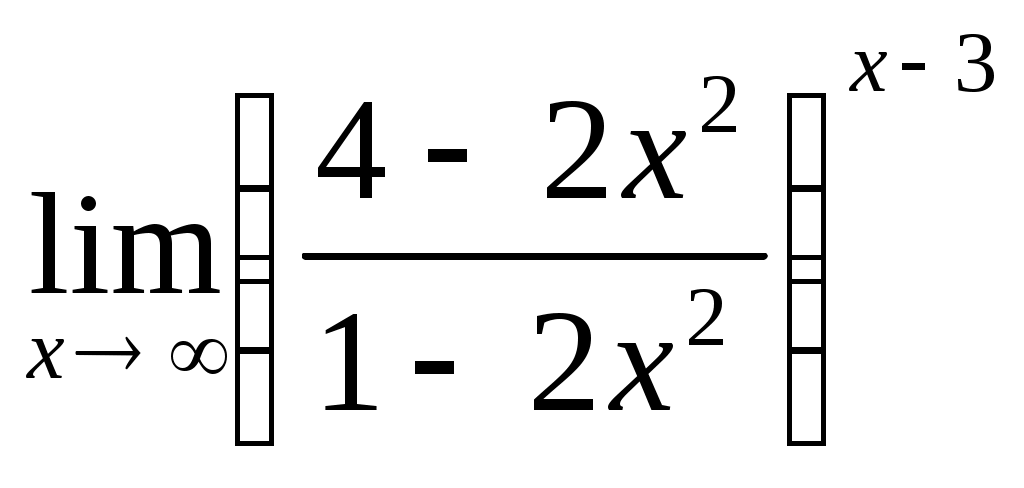 .
.
2.1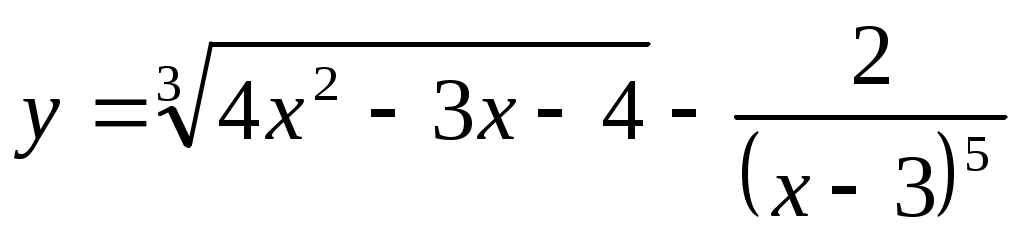 ;
;
2.2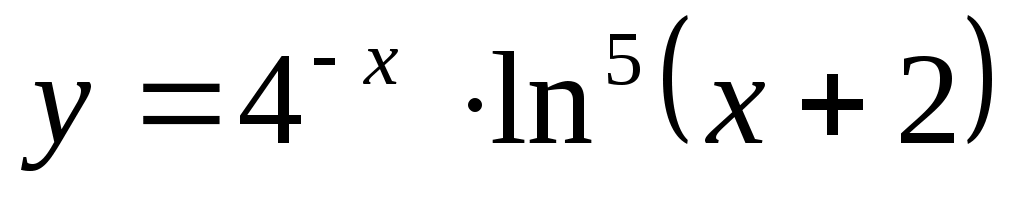 ;
;
2.3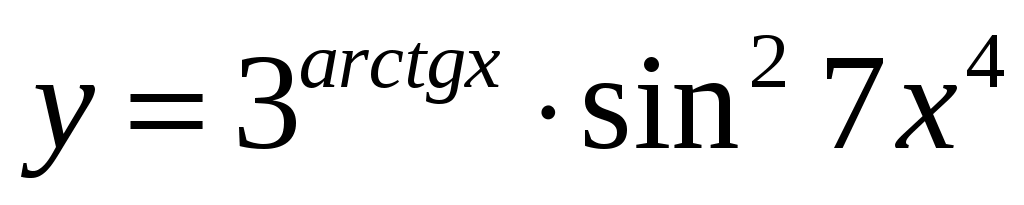 .
.
3.1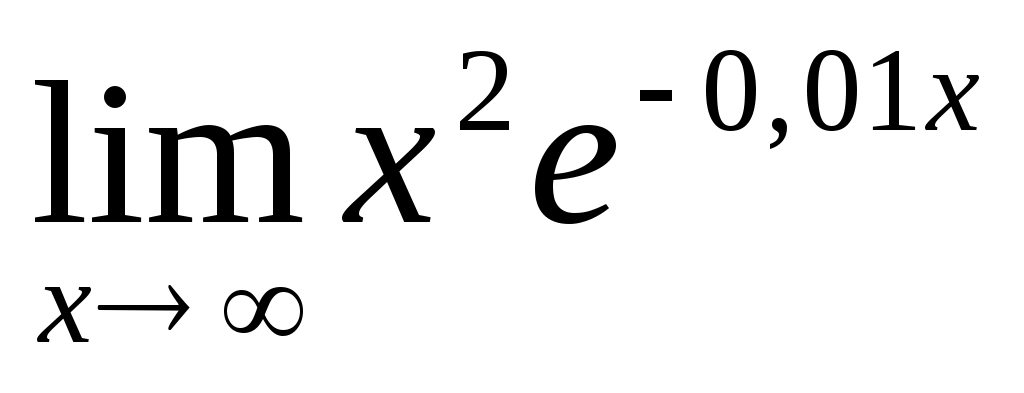 ; 3.2
; 3.2 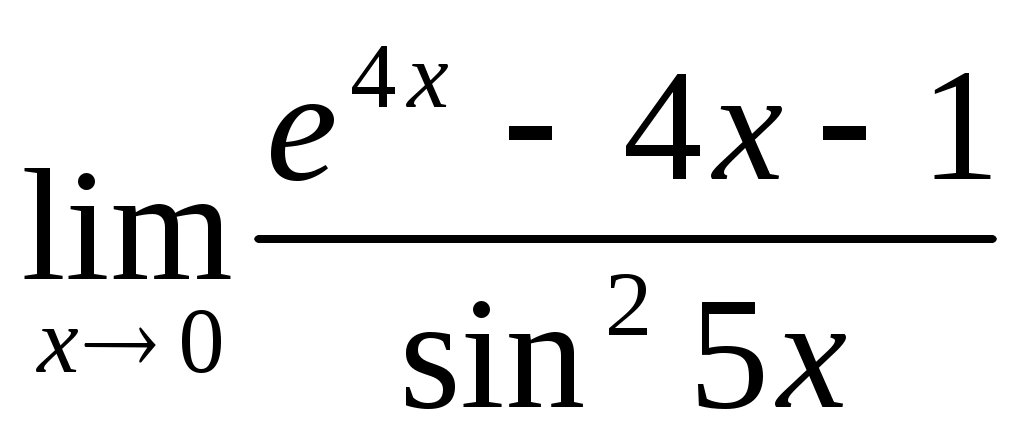 .
.
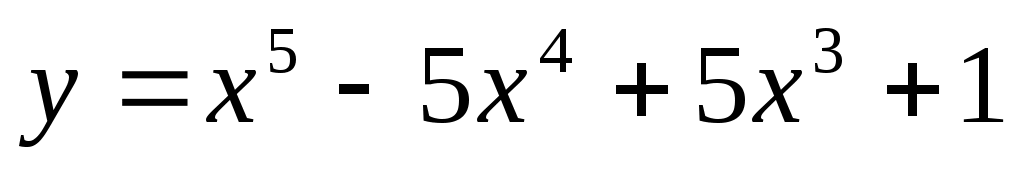 на отрезке [-1, 2].
на отрезке [-1, 2].
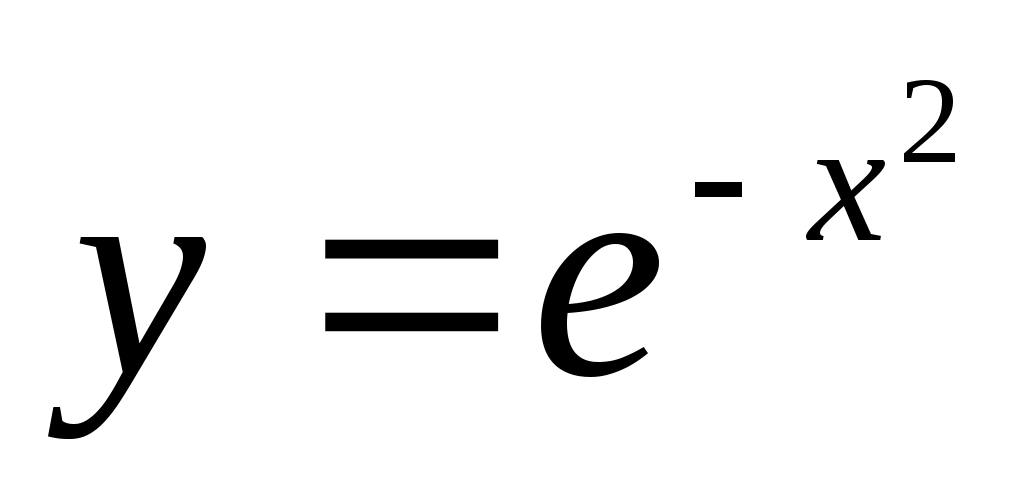 .
.
Вариант № 16
1.1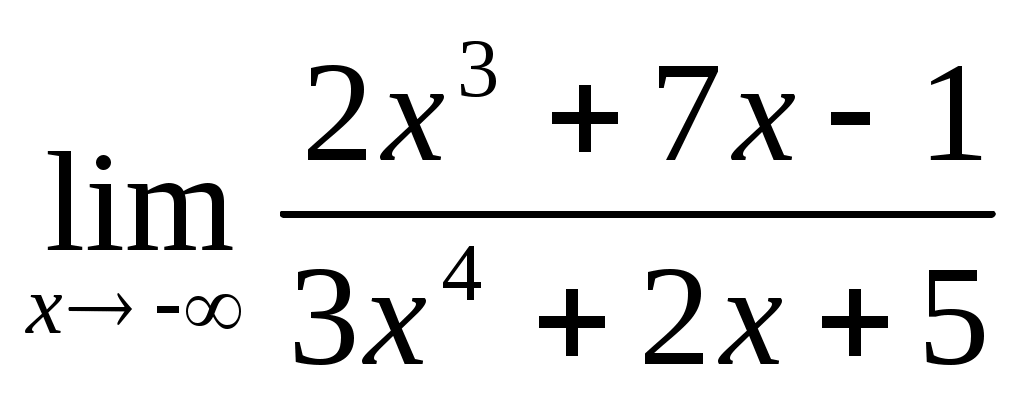
; 1.2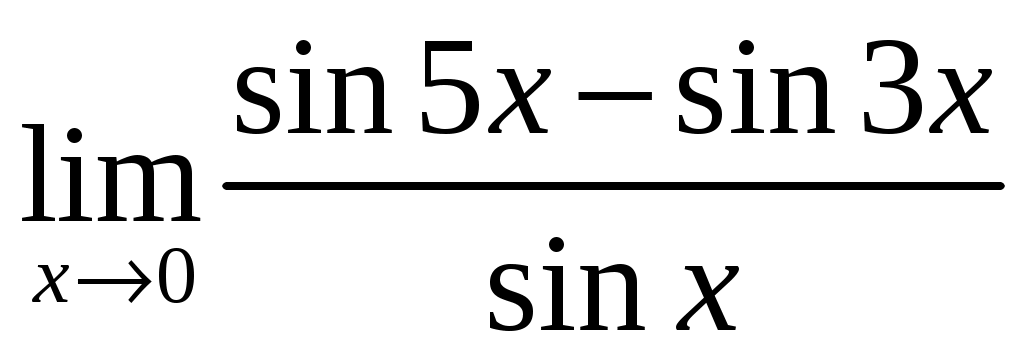 ;
;
1.3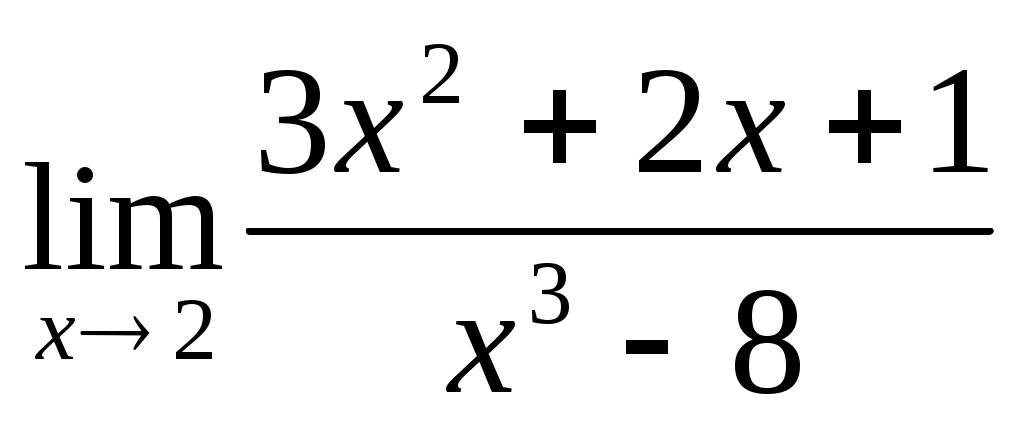 ; 1.4
; 1.4 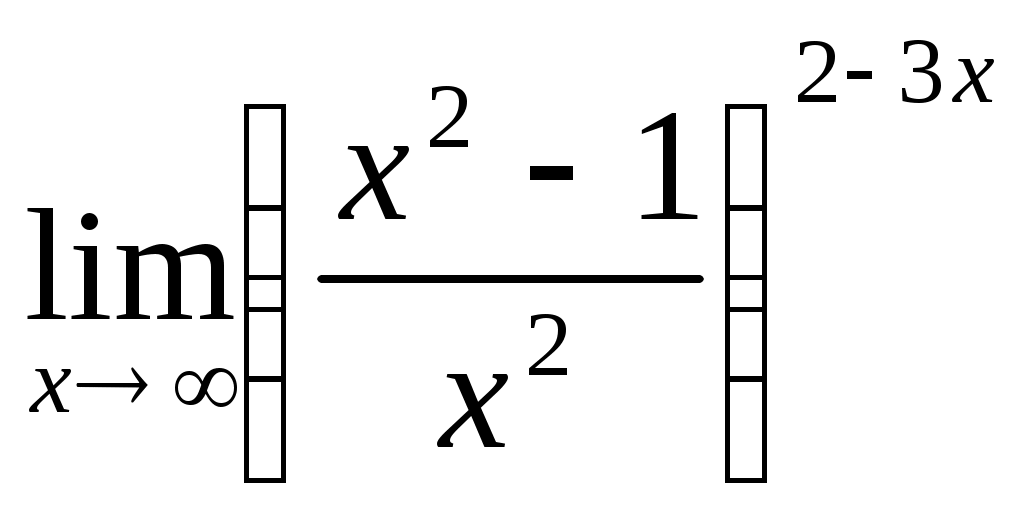 .
.
2.1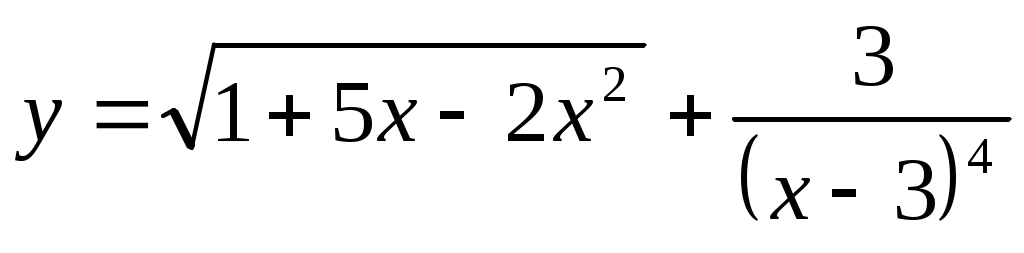 ;
;
2.2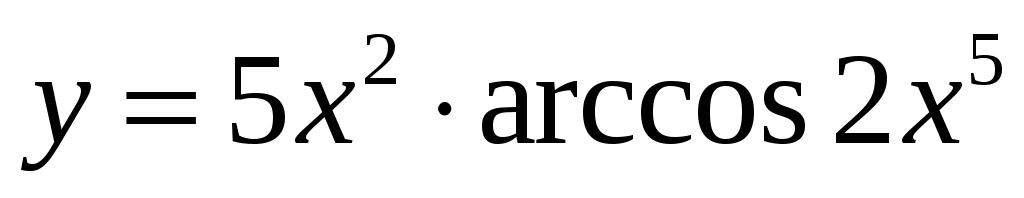 ;
;
2.3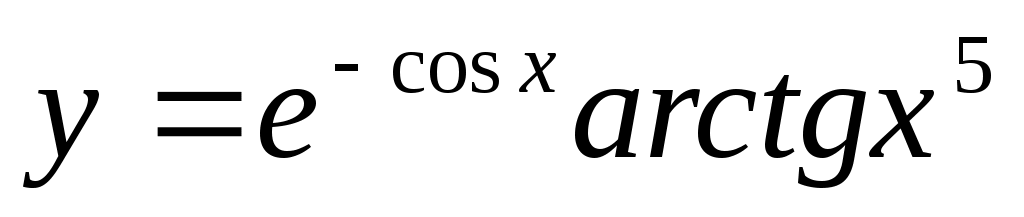 .
.
3.1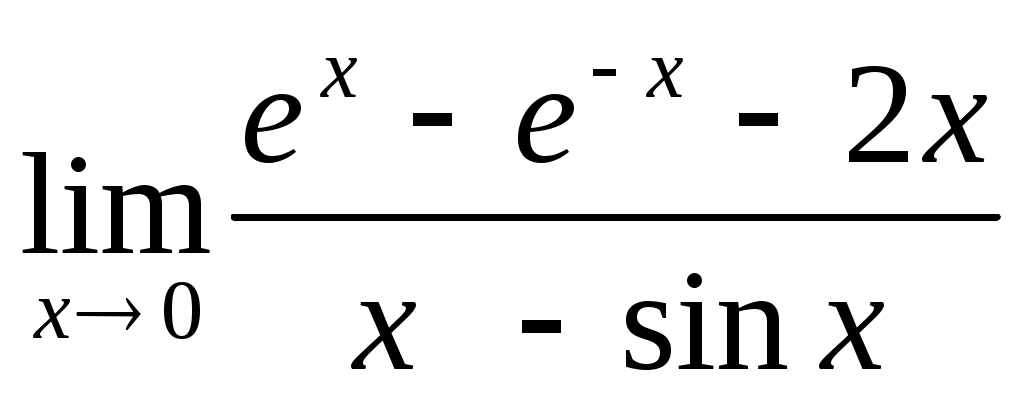 ; 3.2
; 3.2 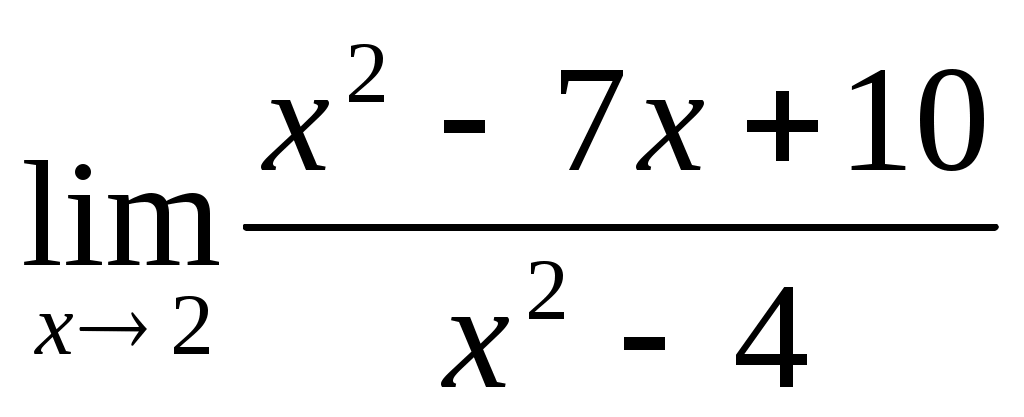 .
.
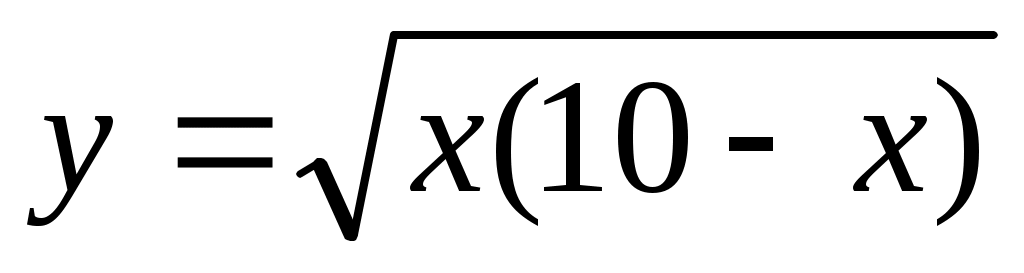 на отрезке [0, 10].
на отрезке [0, 10].
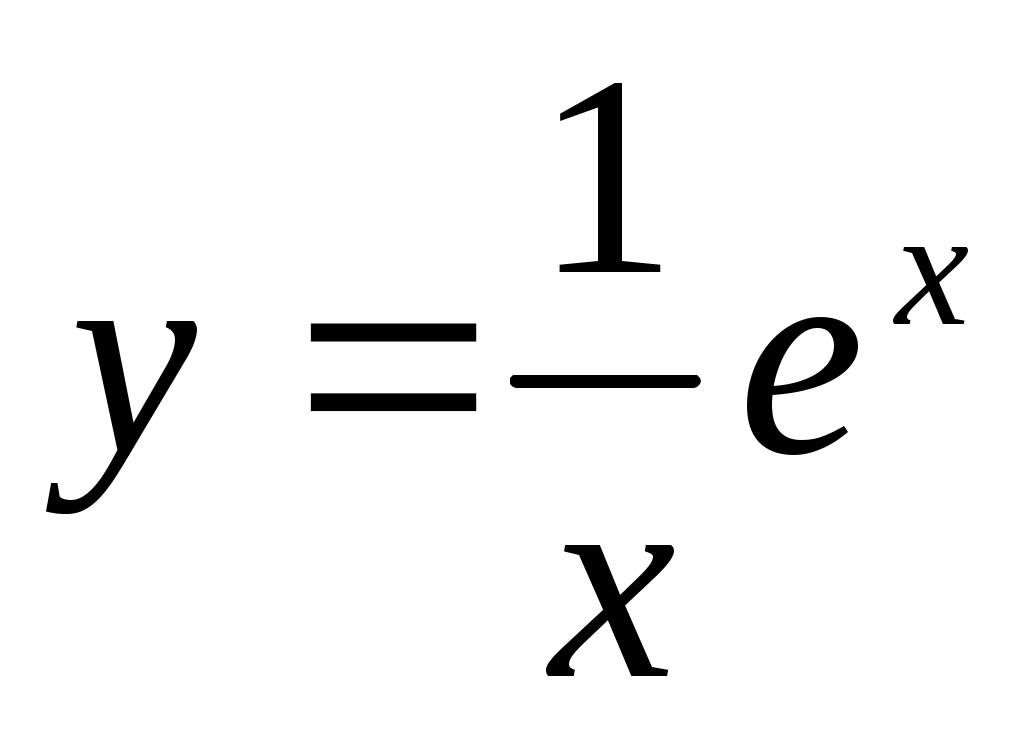 .
.
Вариант № 17
1.1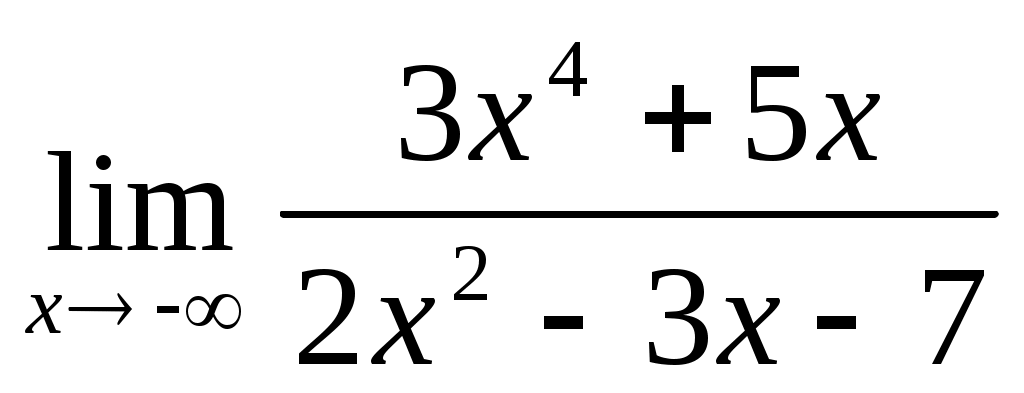 ; 1.2
; 1.2 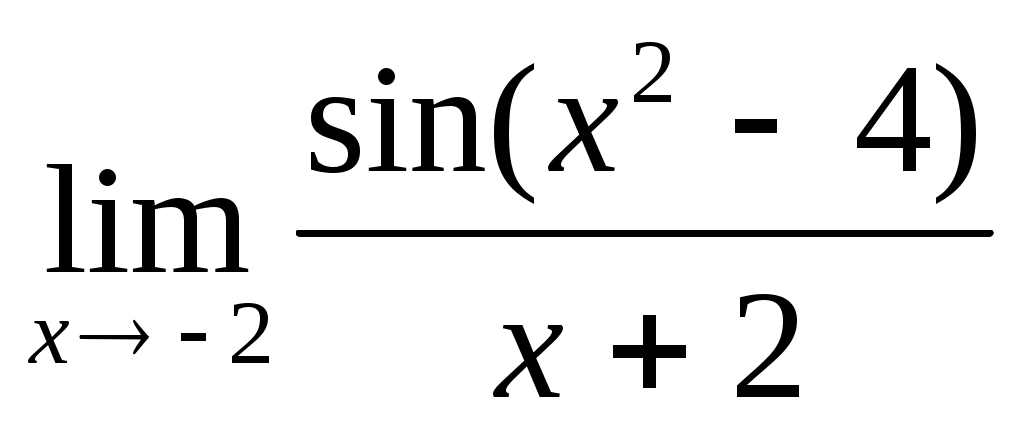 ;
;
1.3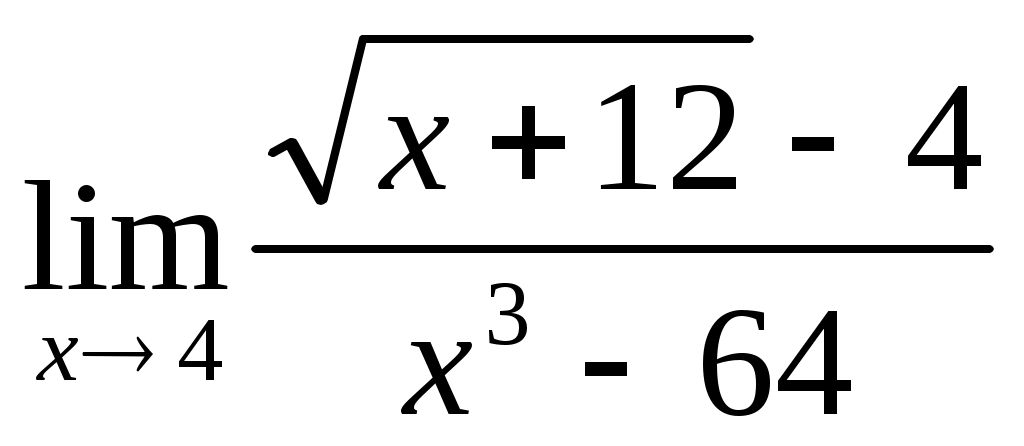 ; 1.4
; 1.4 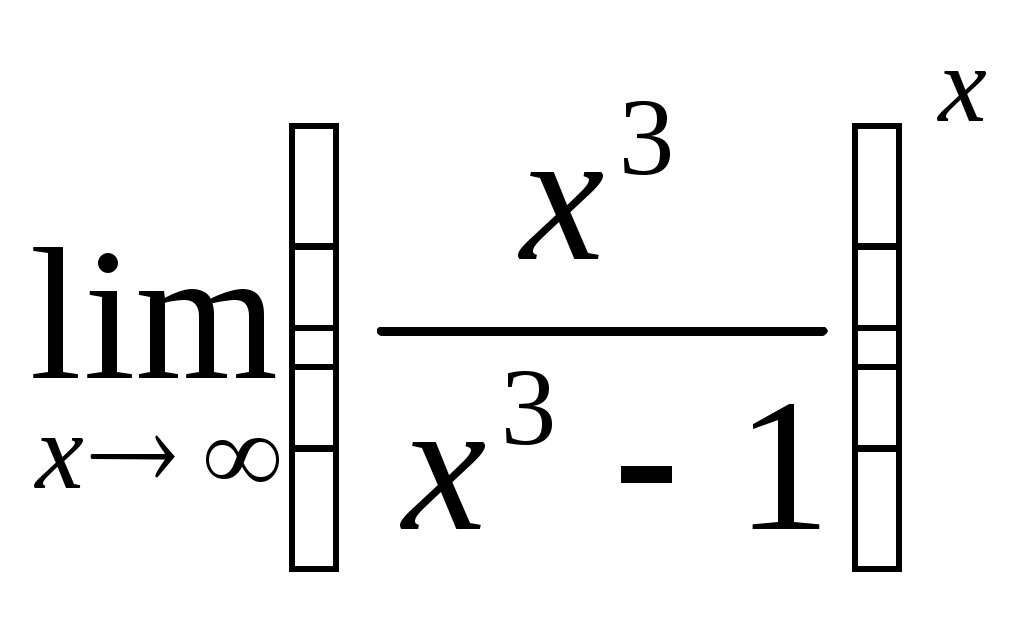 .
.
2.1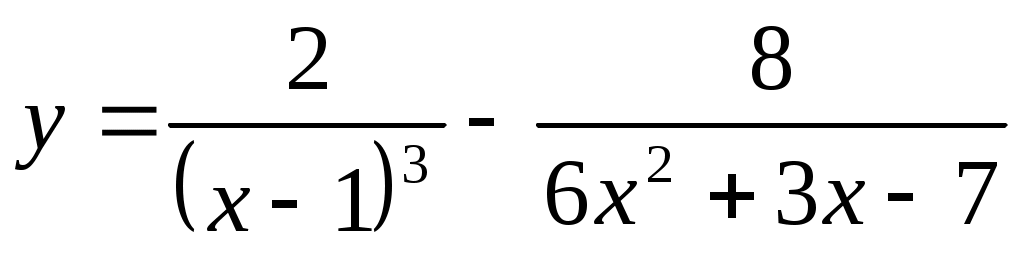 ;
;
2.2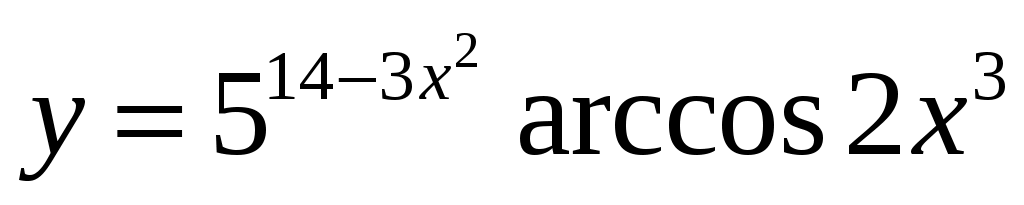 ;
;
2.3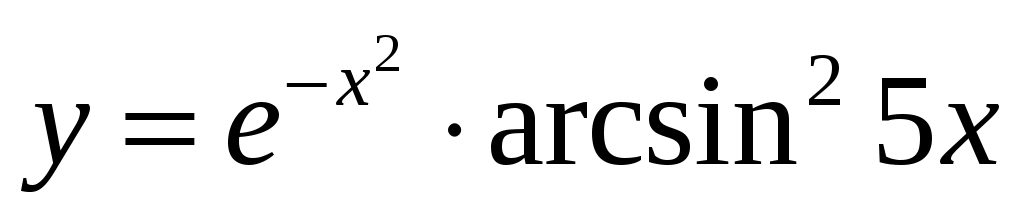 .
.
3.1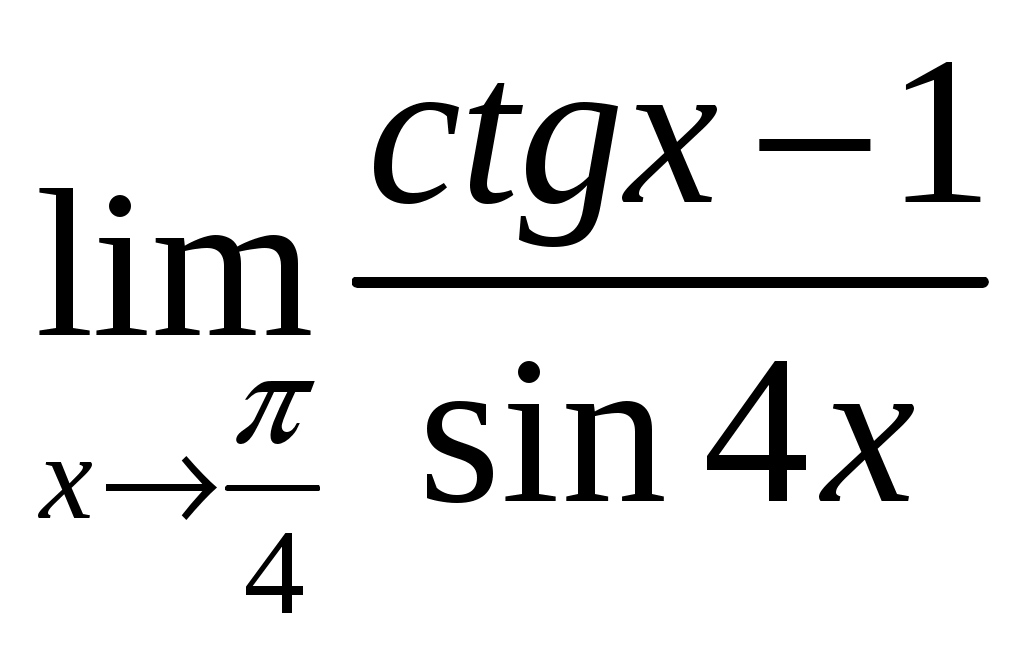
; 3.2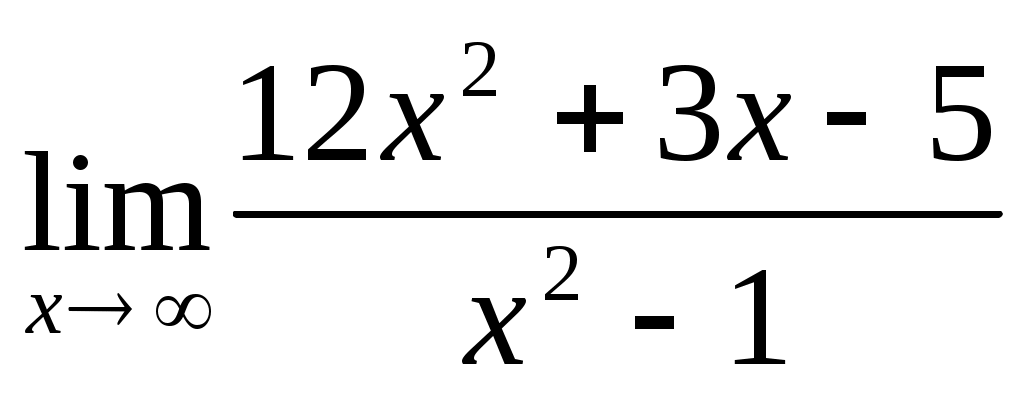 .
.
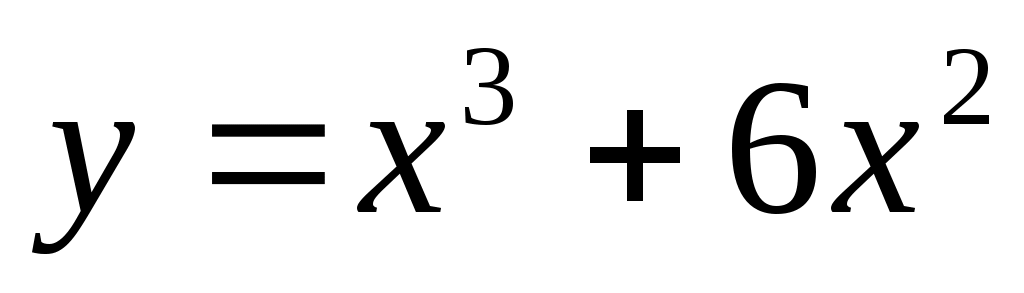 на отрезке [-3, 1].
на отрезке [-3, 1].
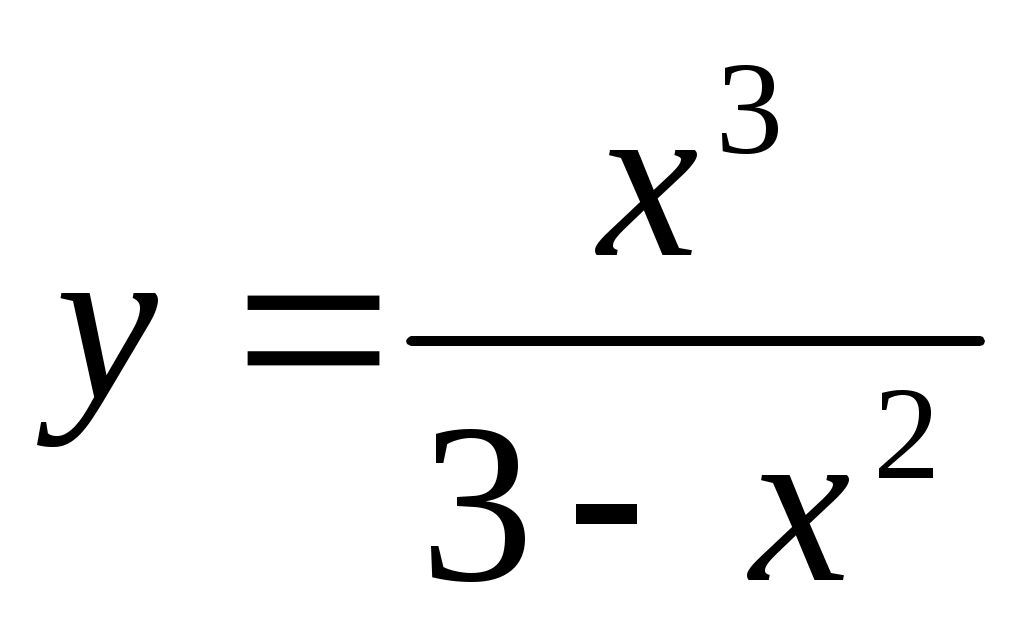 .
.
Вариант № 18
1.1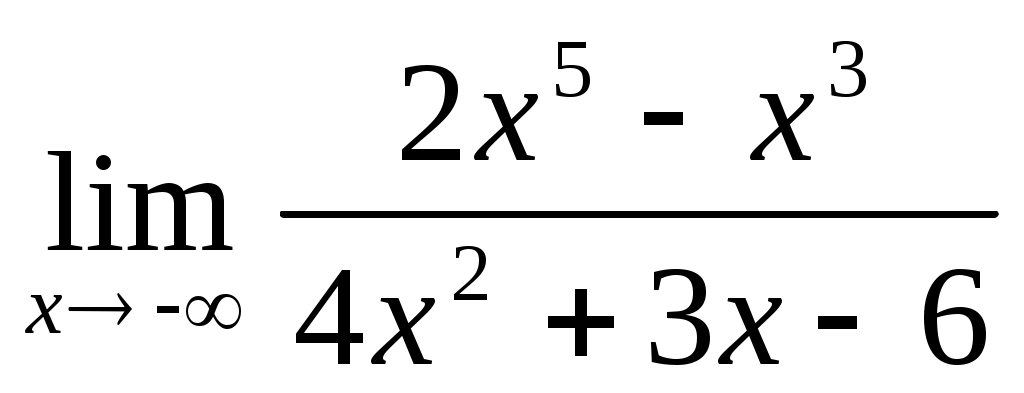 ; 1.2
; 1.2 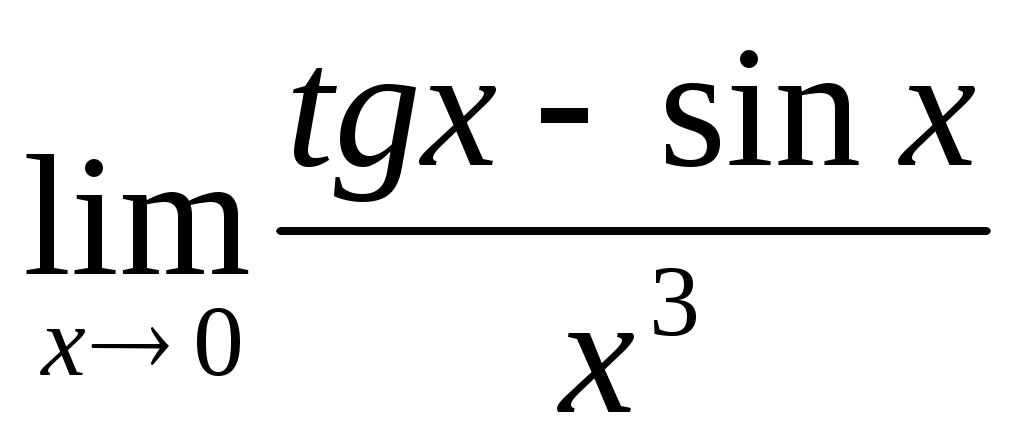 ;
;
1.3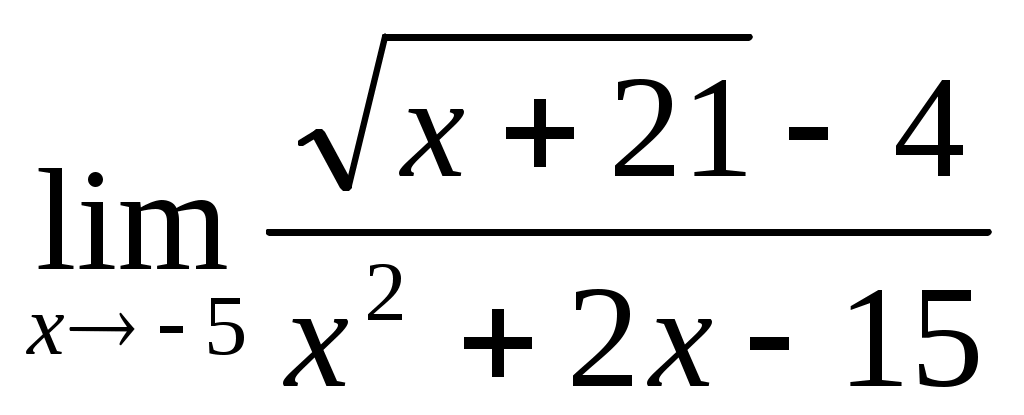 ; 1.4
; 1.4 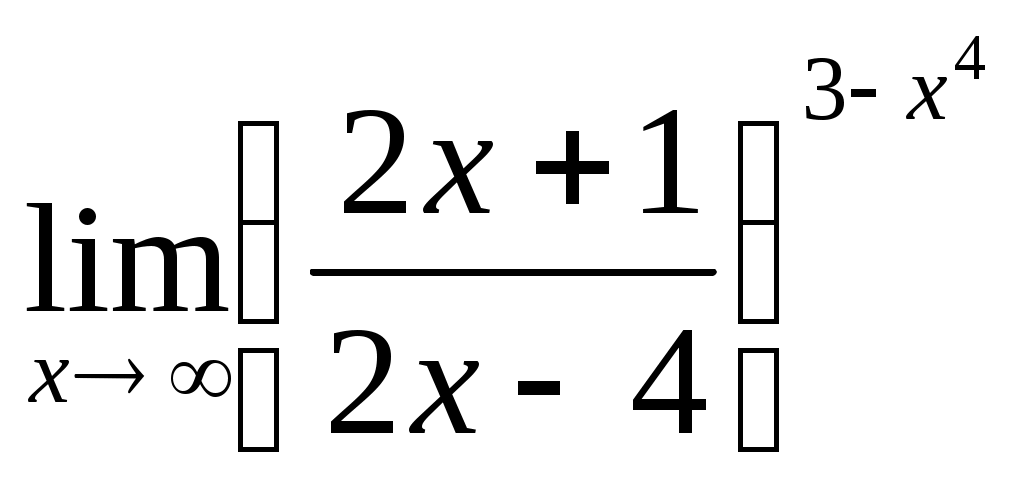 .
.
2.1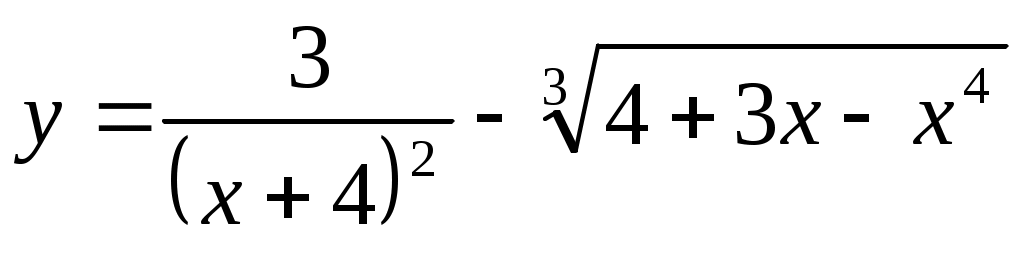 ;
;
2.2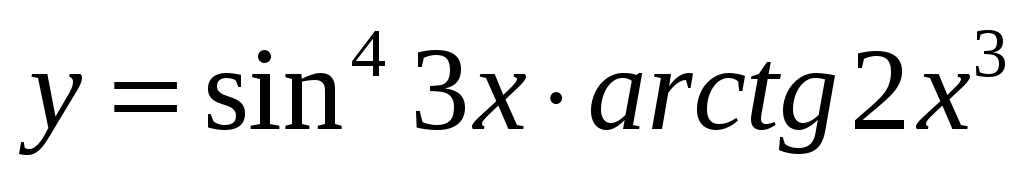 ;
;
2.3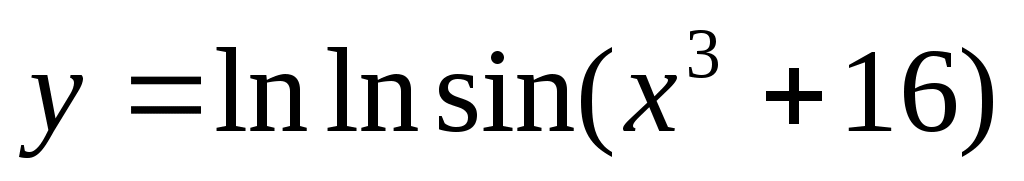 .
.
3.1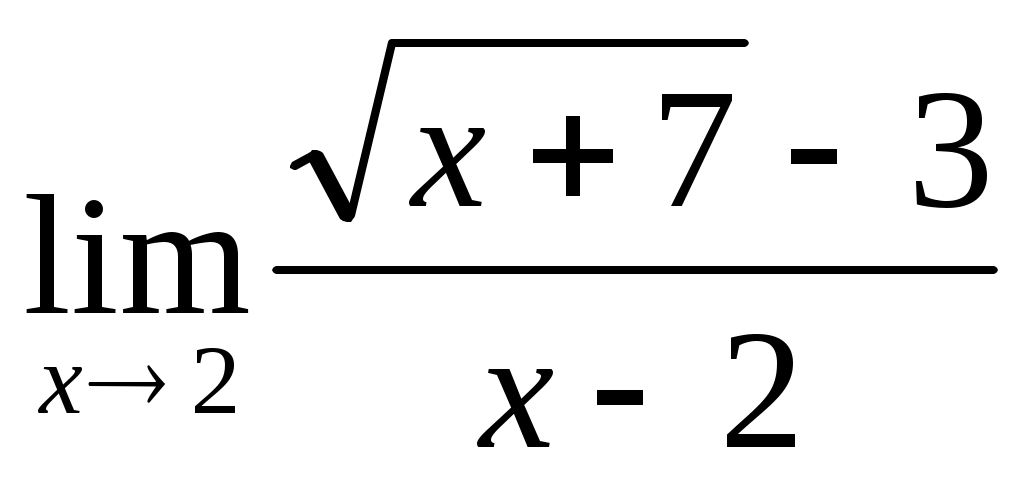 ; 3.2
; 3.2 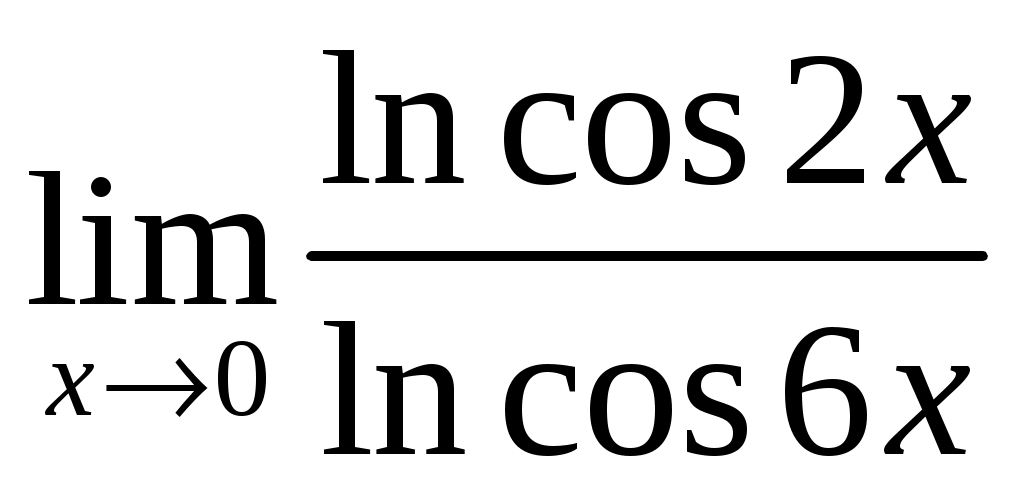 .
.
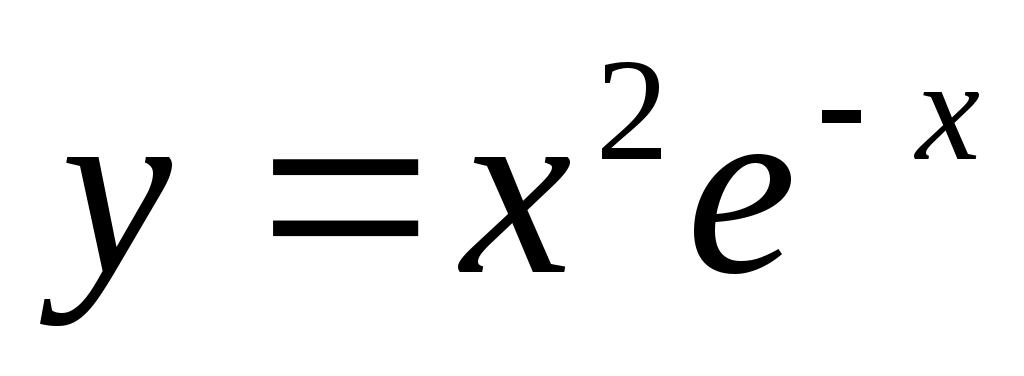 на отрезке [-1, 3].
на отрезке [-1, 3].
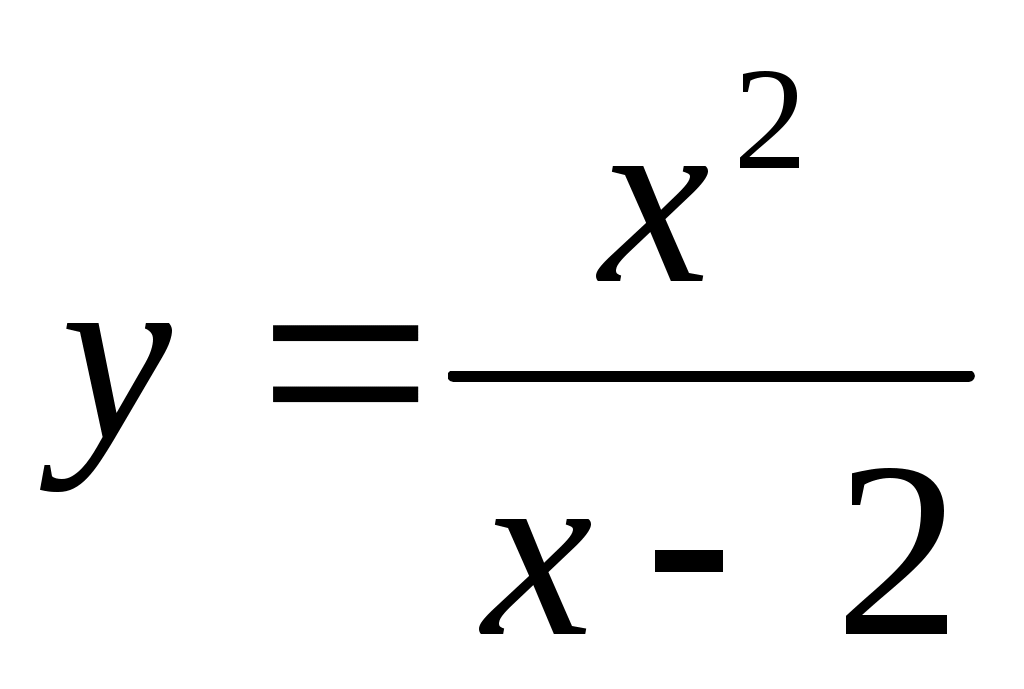 .
.
Вариант № 19
1.1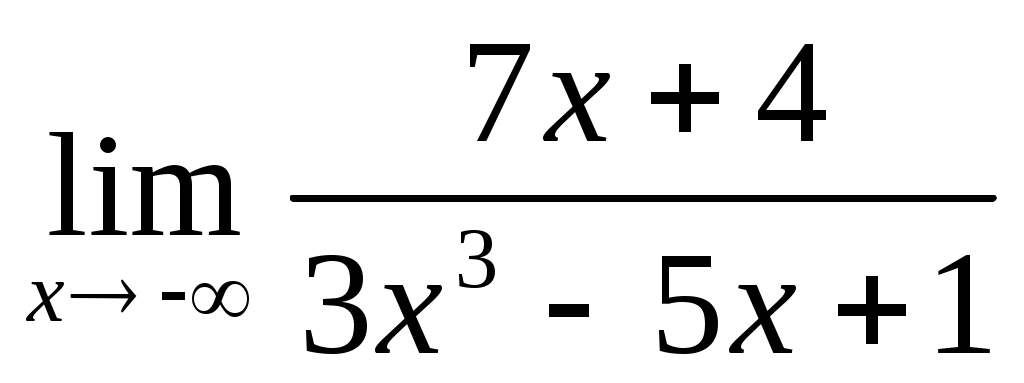 ; 1.2
; 1.2  ;
;
1.3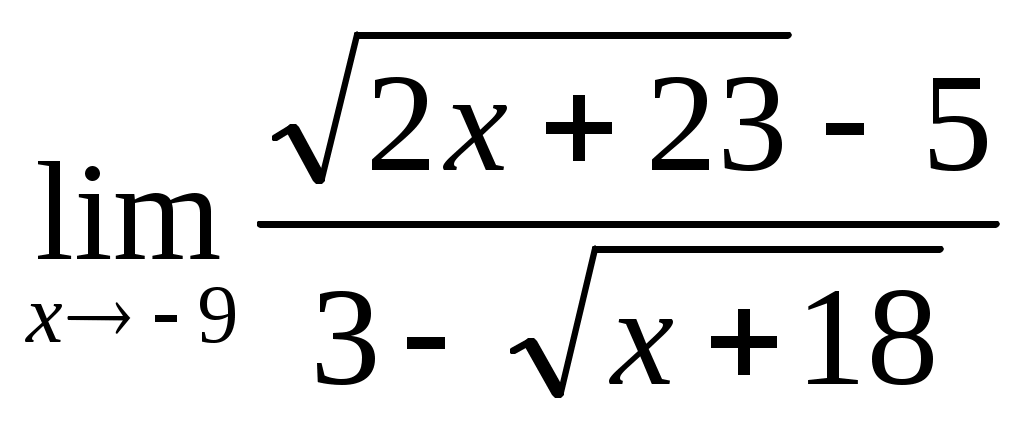 ; 1.4
; 1.4 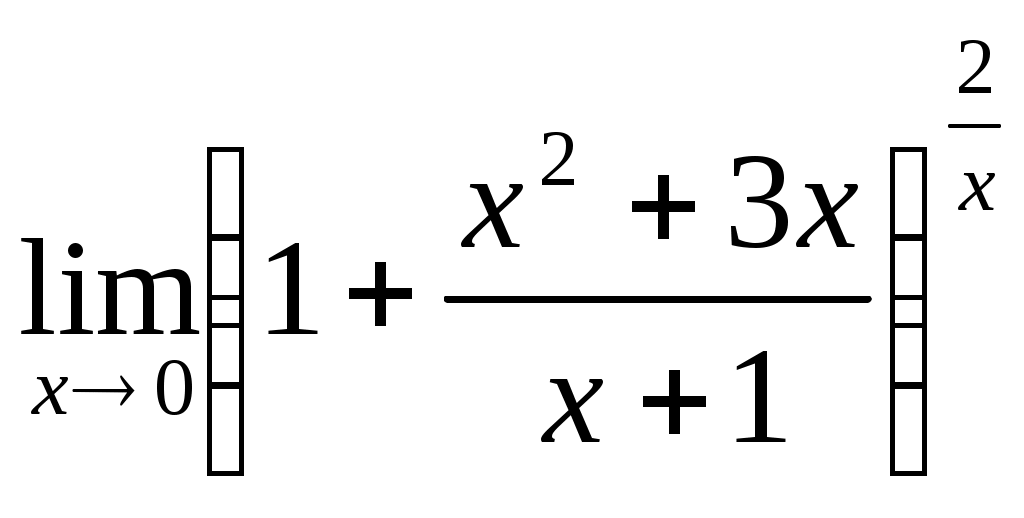 .
.
2.1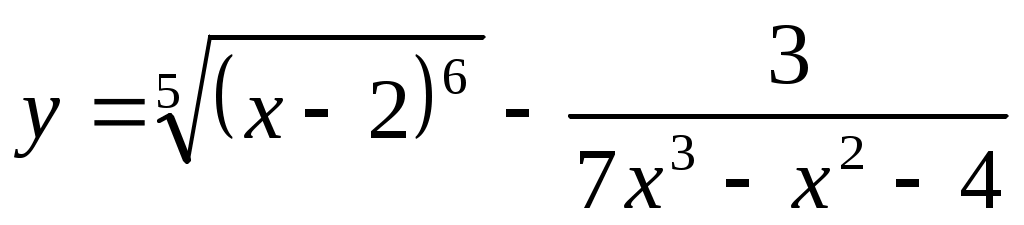 ;
;
2.2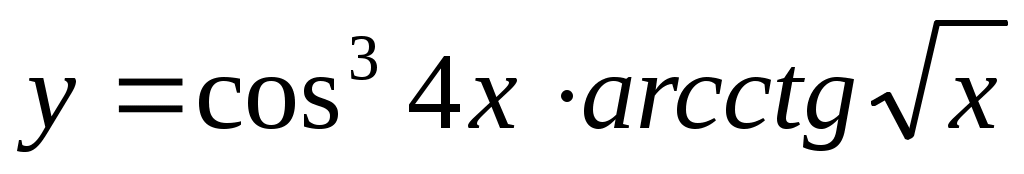 ;
;
2.3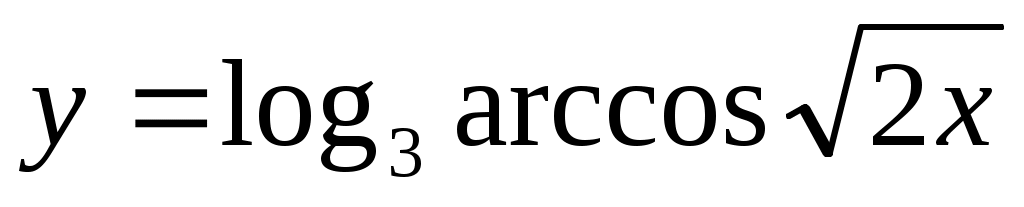 .
.
3.1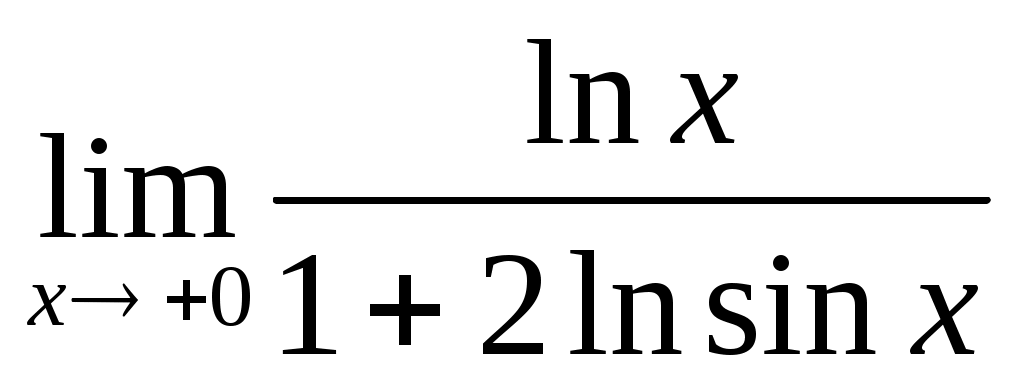 ; 3.2
; 3.2 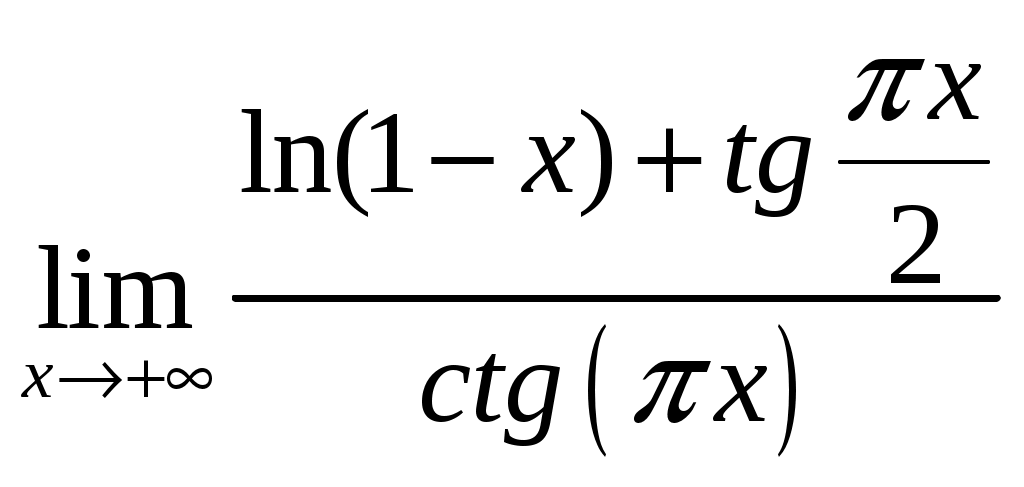 .
.
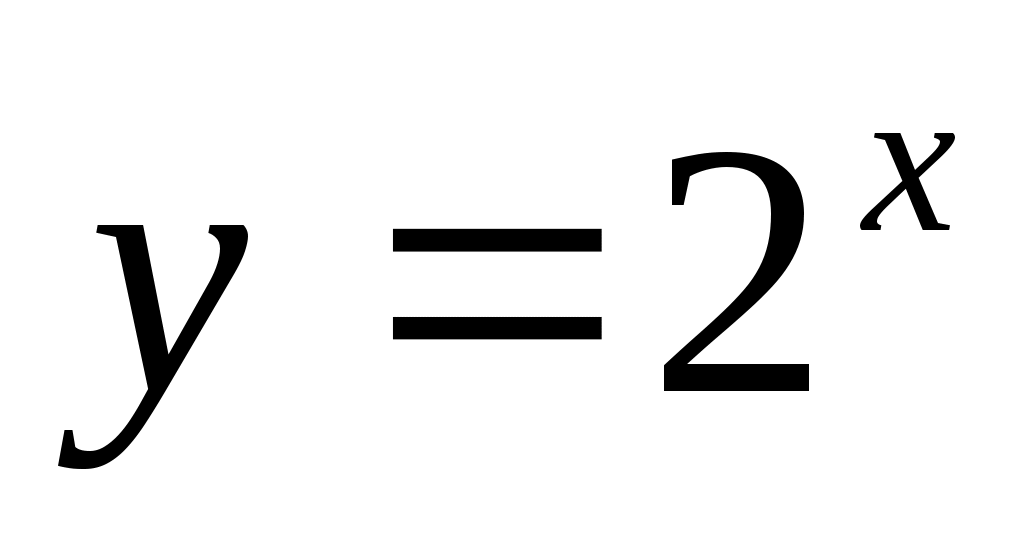 на отрезке [-1, 5].
на отрезке [-1, 5].
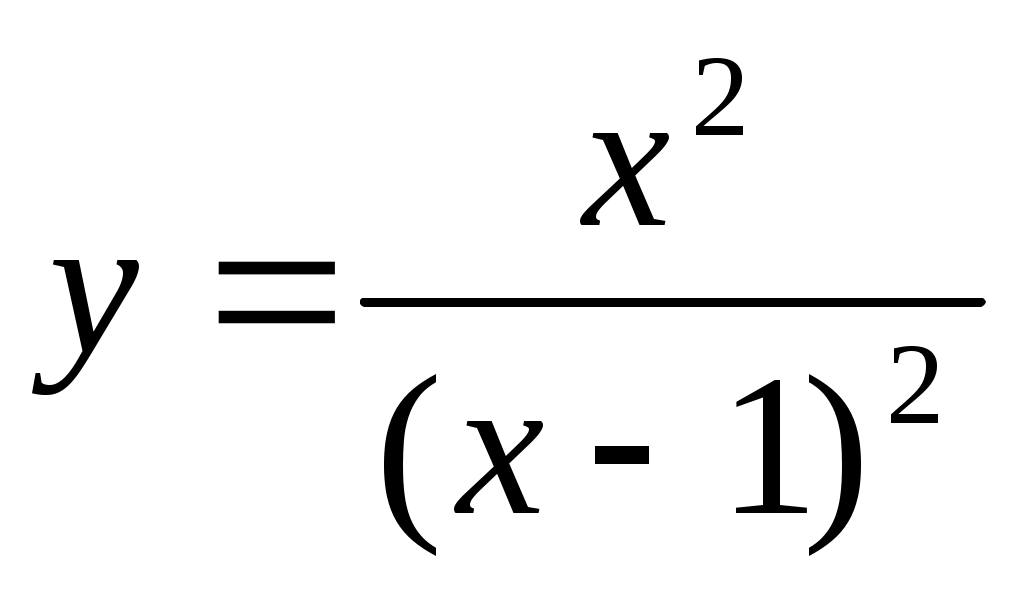 .
.
Вариант № 20
1.1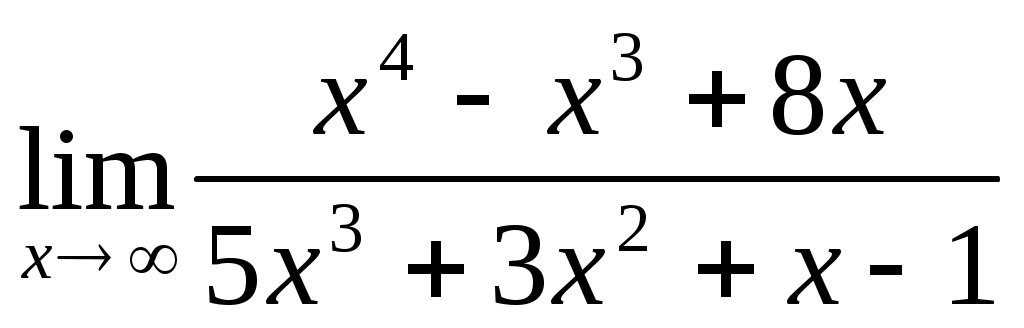 ; 1.2
; 1.2 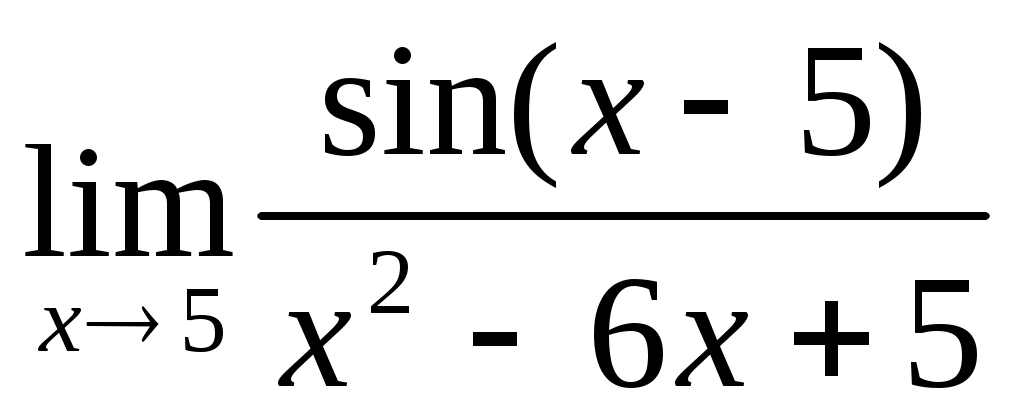 ;
;
1.3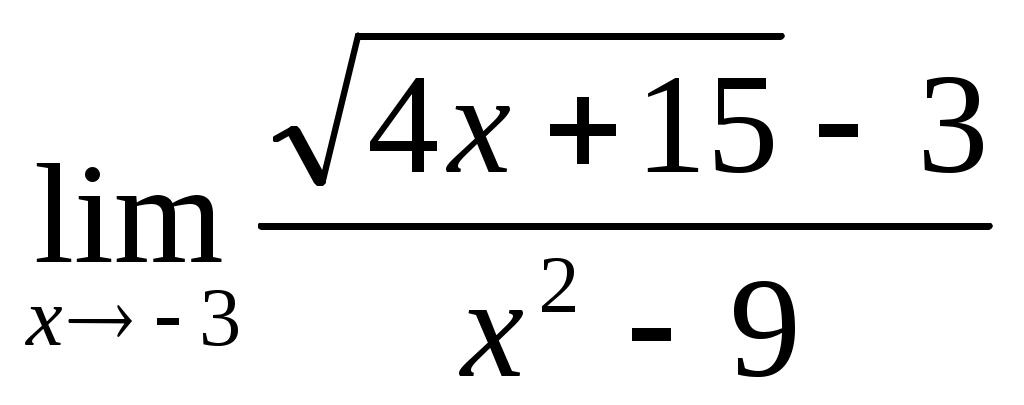 ; 1.4
; 1.4 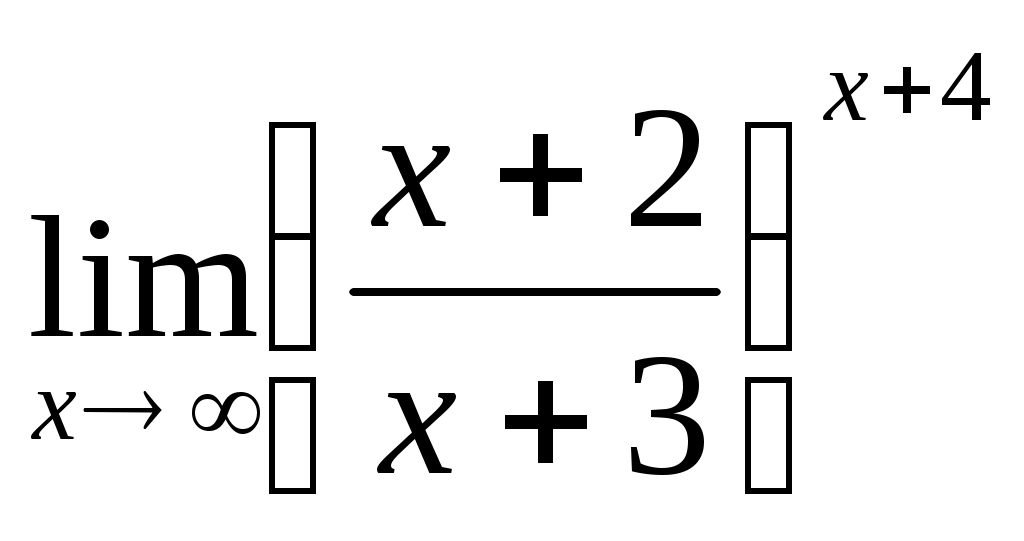 .
.
2.1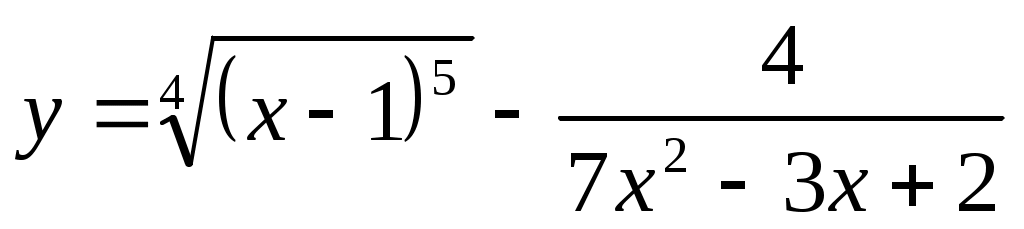 ;
;
2.2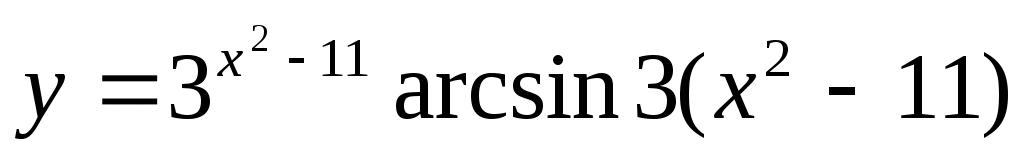 ;
;
2.3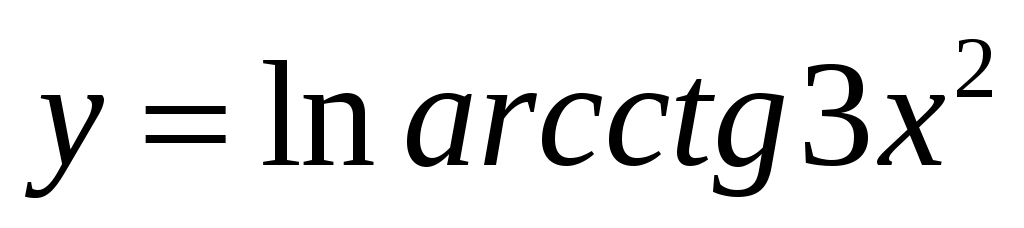
.
3.1 ; 3.2
; 3.2 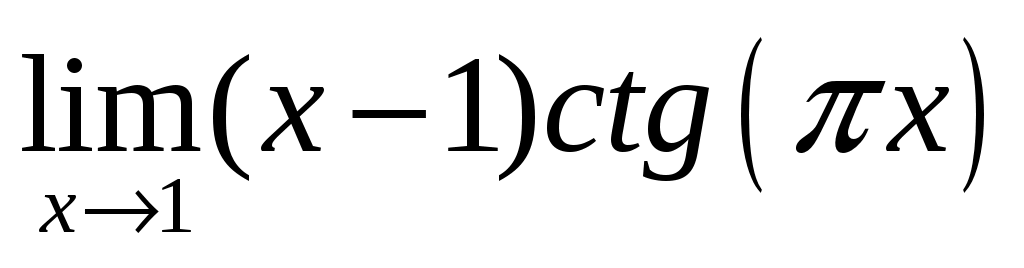 .
.
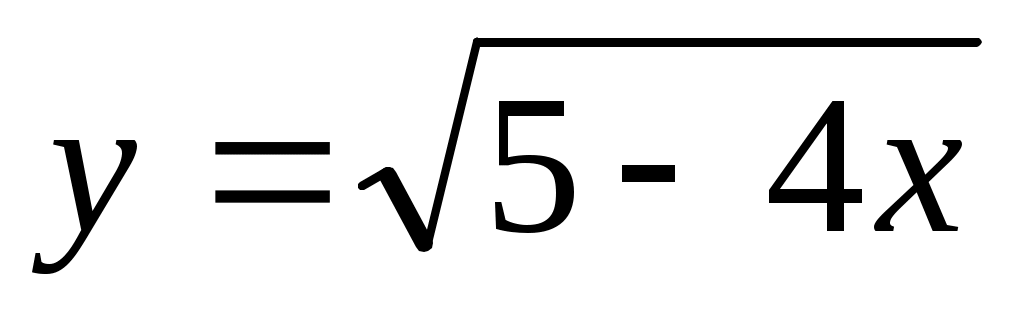 на отрезке [-1; 1].
на отрезке [-1; 1].
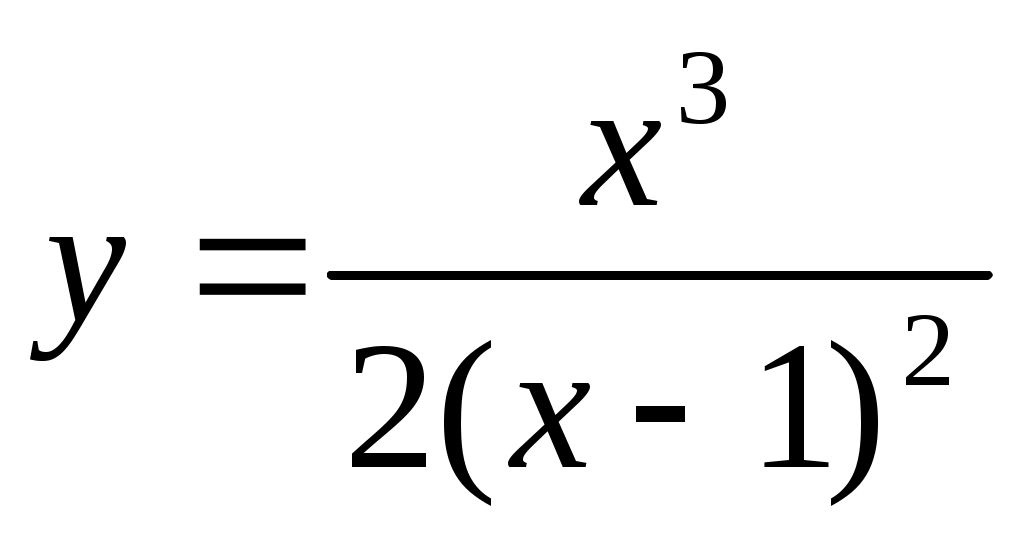 .
.
Вариант № 21
1.1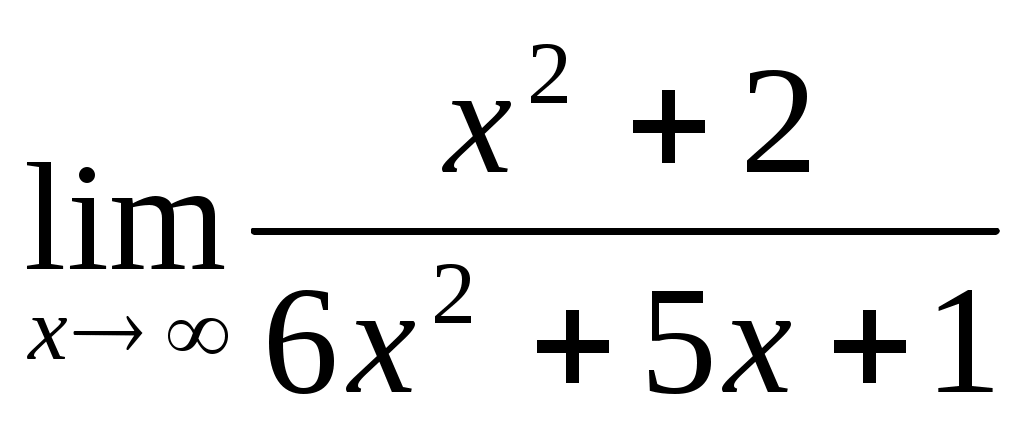 ; 1.2
; 1.2 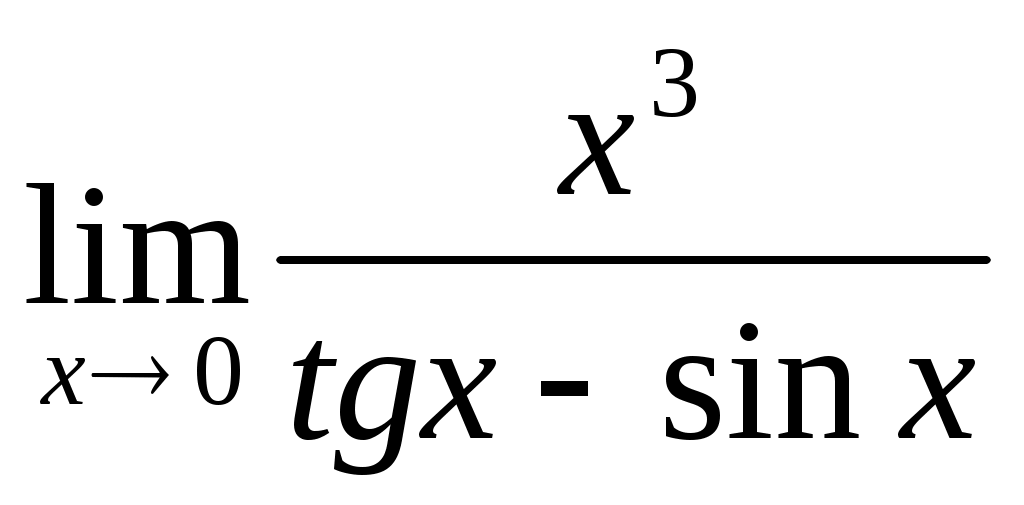 ;
;
1.3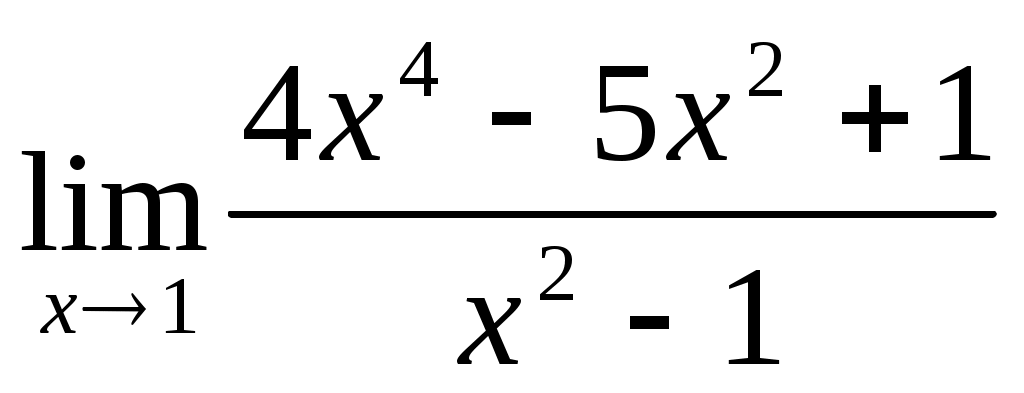 ; 1.4
; 1.4 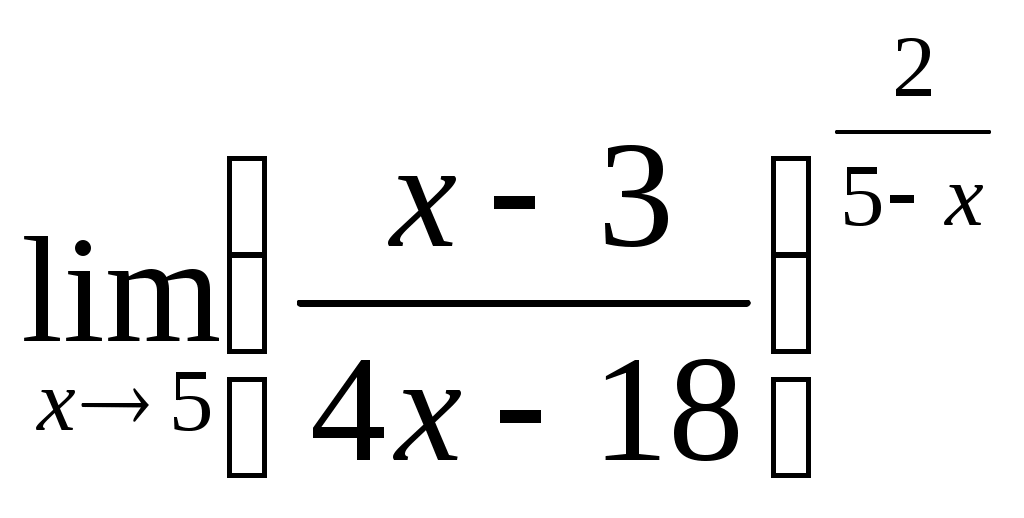 .
.
2.1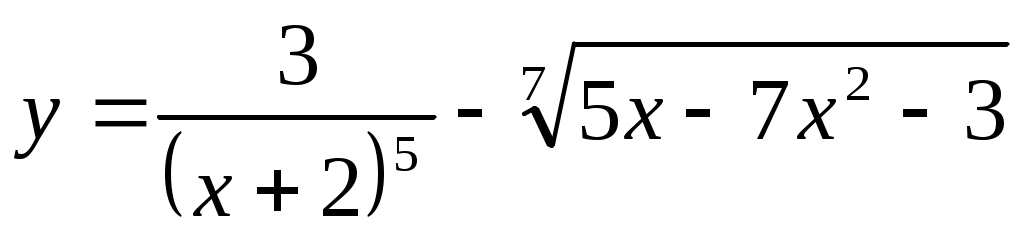 ;
;
2.2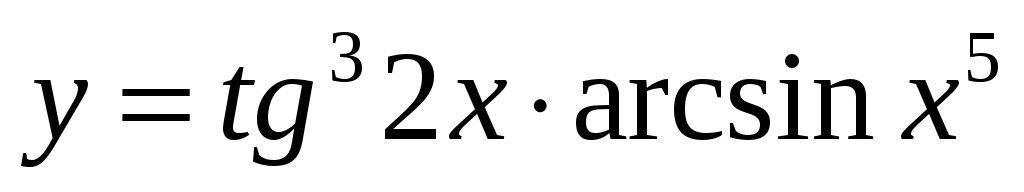 ;
;
2.3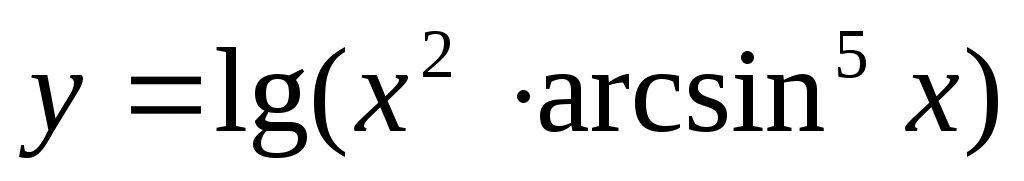 .
.
3.1 ; 3.2
; 3.2 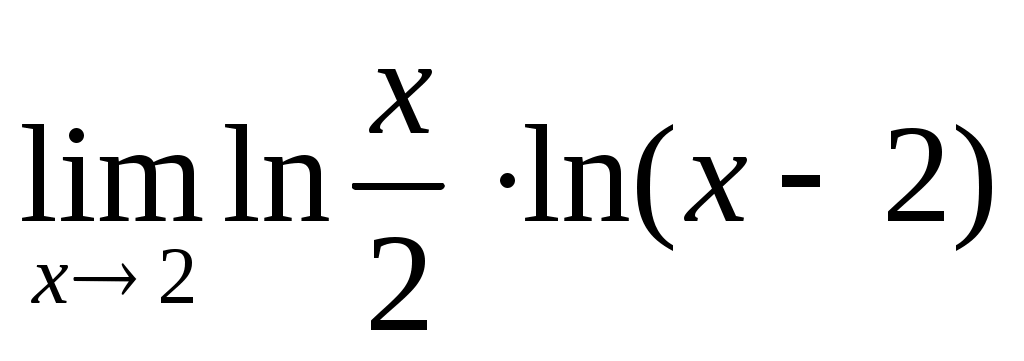 .
.
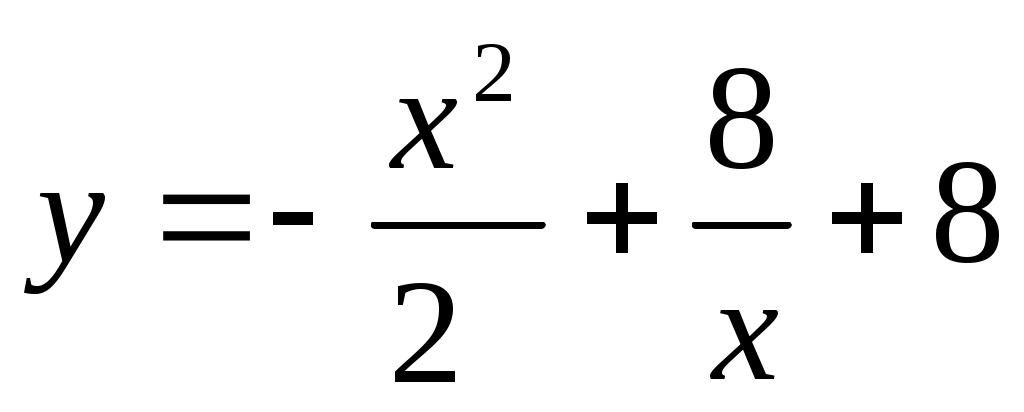 на отрезке [-4, -1].
на отрезке [-4, -1].
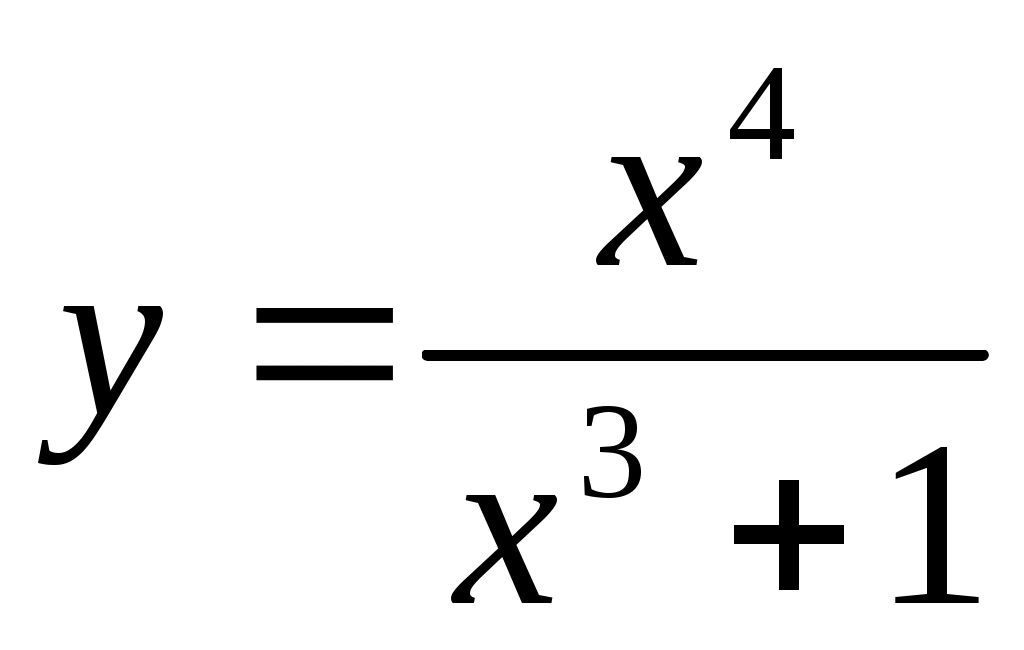 .
.
Вариант № 22
1.3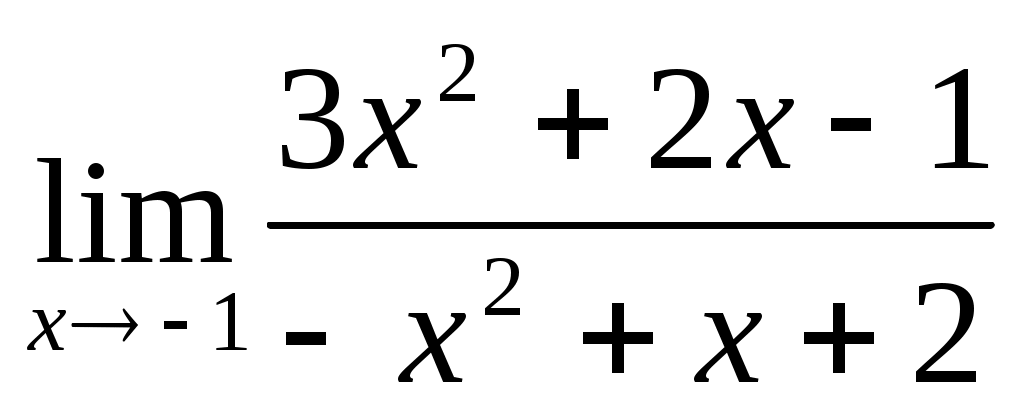 ; 1.4
; 1.4
2.3
-
Найти пределы функций, используя правило Лопиталя:
3.1
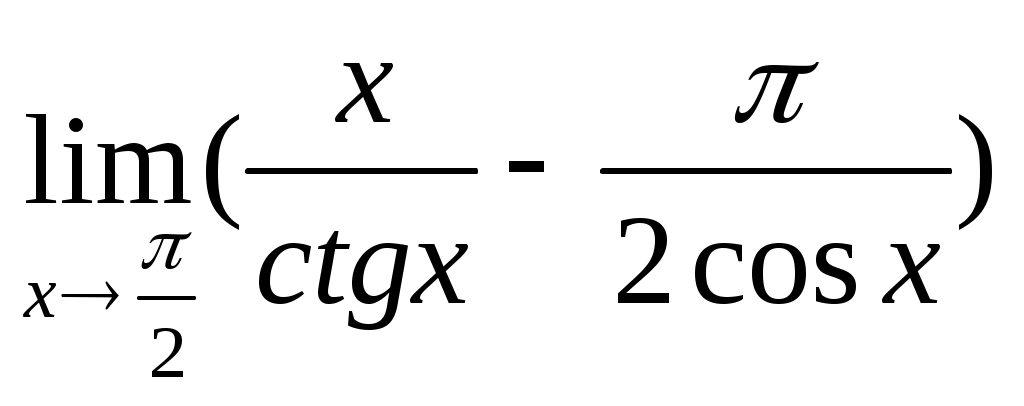 .
.-
Найти наибольшее и наименьшее значения функции
-
Провести полное исследование функции и построить ее график:
Вариант № 15
-
Вычислить пределы, не используя правило Лопиталя:
1.1
1.3
-
Найти производные функций:
2.1
2.2
2.3
-
Найти пределы функций, используя правило Лопиталя:
3.1
-
Найти наибольшее и наименьшее значения функции
-
Провести полное исследование функции и построить ее график:
Вариант № 16
-
Вычислить пределы, не используя правило Лопиталя:
1.1
; 1.2
1.3
-
Найти производные функций:
2.1
2.2
2.3
-
Найти пределы функций, используя правило Лопиталя (если оно применимо в данном случае):
3.1
-
Найти наибольшее и наименьшее значения функции
-
Провести полное исследование функции и построить ее график:
Вариант № 17
-
Вычислить пределы, не используя правило Лопиталя:
1.1
1.3
-
Найти производные функций:
2.1
2.2
2.3
-
Найти пределы функций, используя правило Лопиталя (если оно применимо в данном случае):
3.1
; 3.2
-
Найти наибольшее и наименьшее значения функции
-
Провести полное исследование функции и построить ее график:
Вариант № 18
-
Вычислить пределы, не используя правило Лопиталя:
1.1
1.3
-
Найти производные функций:
2.1
2.2
2.3
-
Найти пределы функций, используя правило Лопиталя (если оно применимо в данном случае):
3.1
-
Найти наибольшее и наименьшее значения функции
-
Провести полное исследование функции и построить ее график:
Вариант № 19
-
Вычислить пределы, не используя правило Лопиталя:
1.1
1.3
-
Найти производные функций:
2.1
2.2
2.3
-
Найти пределы функций, используя правило Лопиталя (если оно применимо в данном случае):
3.1
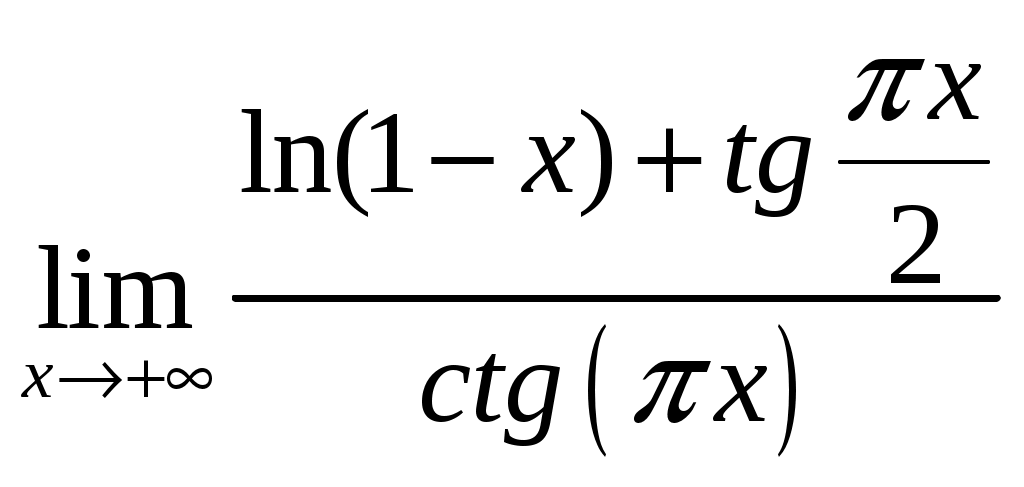 .
.-
Найти наибольшее и наименьшее значения функции
-
Провести полное исследование функции и построить ее график:
Вариант № 20
-
Вычислить пределы, не используя правило Лопиталя:
1.1
1.3
-
Найти производные функций:
2.1
2.2
2.3
.
-
Найти пределы функций, используя правило Лопиталя
3.1
-
Найти наибольшее и наименьшее значения функции
-
Провести полное исследование функции и построить ее график:
Вариант № 21
-
Вычислить пределы, не используя правило Лопиталя:
1.1
1.3
-
Найти производные функций:
2.1
2.2
2.3
-
Найти пределы функций, используя правило Лопиталя:
3.1
-
Найти наибольшее и наименьшее значения функции
-
Провести полное исследование функции и построить ее график:
Вариант № 22
-
Вычислить пределы, не используя правило Лопиталя:
1.3