Целевая функция

Ячейка

Имя

Значение

$D$6

1,2

Переменная

Нижний

Целевая функция

Верхний

Целевая функция

Ячейка

Имя

Значение

Предел

Результат

Предел

Результат

$A$4

х1

0,6

0,6

1,2

#Н/Д

#Н/Д

$B$4

х2

0

0

1,2

1,9

6,9

х1

х2

0,6

0

3

≥

3

-2,4

≤

9

1,2

мин

---

Практическая работа 3

1. 
   Какие задачи линейного программирования называются транспортными?
   

К ЗЛП транспортного типа (кратко: транспортной задаче− ТЗ) приходят при рассмотрении различных практических ситуаций, связанных с составлением наиболее экономичного плана перевозок продукции, управления запасами, назначением персонала на рабочие места, оборотом наличного капитала и многими другими.

2. 
   Каковы особенности математической модели транспортной задачи?
   

Особенности экономико-математической модели транспортной задачи:

• система ограничений есть система уравнений (т.е. транспортная задача задана в канонической форме);

• коэффициенты при переменных системы ограничений равны единице или нулю;

• каждая переменная входит в систему ограничений два раза.

3. 
   Какие транспортные задачи называются открытыми и закрытыми?
   

Закрытая задача характеризуется тем, что суммарная потребность всех потребителей равна суммарным запасам всех складов. То есть, весь товар на всех складах будет реализован полностью.

В открытой задаче суммарная потребность и суммарные запасы не совпадают. Например, какой-то склад не реализуется товар полностью, появляются остатки продукции. В этом случае процесс решения транспортной задачи немного усложняется, потребуется ввести фиктивного поставщика или потребителя с нулевыми стоимостями перевозки.

4. 
   Могут ли объемы перевозок быть отрицательными?
   

Объемы перевозок не могут быть отрицательными

---

5. В чем особенность целевой функции транспортной задачи?

Целевая функция представляет собой общие транспортные расходы на осуществление всех перевозок в целом. Первая группа ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта. Вторая группа ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворить спрос на продукцию в этом пункте.

Ограничения, препятствующие существованию допустимого решения задачи
	Ячейка	Имя	Значение ячейки	Формула	Состояние	Допуск
	$G$4	А2 Запасы,т	330	$G$4=$G$11	Нарушены	-330
	$G$5	А3 Запасы,т	270	$G$5=$G$12	Нарушены	-270

Ограничения, не включая переменные границы, препятствующие существованию допустимого решения задачи
	Ячейка	Имя	Значение ячейки	Формула	Состояние	Допуск
	$G$4	А2 Запасы,т	330	$G$4=$G$11	Нарушены	-330
	$G$5	А3 Запасы,т	270	$G$5=$G$12	Нарушены	-270

---

	В1	В2	В3	В4	В5	Запасы,т
А1	3	12	9	1	7	350
А2	2	4	11	2	10	330
А3	7	14	12	5	8	270
Потребность	210	170	220	150	200	950
	В1	В2	В3	В4	В5
А1	210	170	0	150	0	150
А2	0	0	0	0	0	0
А3	0	0	220	0	200	0
	210	170	220	150	200	950

---

Практическая работа 4

1. Объясните, в чем суть прогнозирования экономических процессов на основе метода динамических рядов?

Суть экономико – математического метода прогнозирования экономических показателей заключается в построении математических моделей, которые отражают количественные взаимосвязи между показателями

2. Какие компоненты входят в состав динамического ряда?

В состав динамического ряда входят:

- тренд динамического ряда – регулярная компонента, характеризующая общую тенденцию;

- сезонная компонента или внутригодичные колебания, а в общем случае – циклическая составляющая;

- случайная компонента, образующаяся под влиянием различных неизвестных причин;

- компонента, обеспечивающая сопоставимость элементов динамического ряда;

- управляющая компонента, с помощью которой воздействуют на члены динамического ряда с целью формирования в будущем его желаемой траектории (управляемый прогноз).

3. Каким образом происходит расчет каждой из составляющих ряда?

Компонента t Z может быть вычислена как



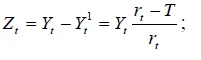
Вычисление регулярной компоненты t U (тренда)

Известны несколько методов вычисления регулярной компоненты. К ним относятся: механические способы сглаживания, аналитические методы с применением определенных математических функций и, наконец, комбинированный способ.

Вычисление сезонной t V и случайной t E компонент

Для определения сезонной и случайной компонент вычисляется динамический ряд

V  E  Y  U  Z , при t n =0.

Нахождение случайной составляющей t E

Временной ряд следует привести к сопоставимому виду, сезонную компоненту и тренд необходимо отфильтровать и вычесть из значений t Y , управление t n должно отсутствовать.

4. Как оценить адекватность трендовой модели?

---

Смотрите также файлы

• Реферат Система обучения и воспитания в иезуитских школах. Мягкова Надежда Андреевна Введение. 1 Определение.docx

• ВыамявмвяпптмЗадание 1 Почему необходимо управление.doc

• Аналитическая справка по итогам итоговой комплексной (метапредметной) диагностики обучающихся 4х классов гбоу оош 11 май 2022 г.doc

• Теория графов, занятие 3.doc

• Муниципальное казённое дошкольное образовательное учреждение Детский сад 6 Ягодка.docx