ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2021
Просмотров: 887
Скачиваний: 4
№9.
e x+l
+jc + - = 0.
5
№10. (x + l)5 +3x + y = 0.
1
11
№13.
(0.5л: - 1)3 + x - — = 0.
№14. e°'5xA
+ 0 . 5 x - - = 0.
V
'
2
2
№15.
(0.5 x- 1)5 + 1 .5 x
- — =
0.
№16.
— ------ V -x + 2 + - =
0.
№17.
ln ( - x + 2 ) - x - | = 0.
№18.
( - x + 2)3 - 2 x + y = 0.
№19. e~x+2
- x + - = 0.
№20. ( - x + 2)5 - 3 x + y = 0.
Образец выполнения задания
Метод итерации
Дано
уравнение
f i x
) = Зх2 - 4х + 7 .
Составим таблицу знаков функции
/ (х) = х 3 - 2х2 + 7х + 3 = 0;
X
-
оо
-1
0
+ оо
f i x )
-
-
+
+
Уравнение
имеет
действительный
корень,
лежащий
в
промежутке [—1;0]. Приведем уравнение к виду х =
(р{х)
так,
чтобы
|^(* )| < 1
ПРИ
- 1 < х < 0 .
Так
как
Q =
т а х |/'(х )| = |/'(~ 1 )| = 14, то можно взять
к =
10 . Тогда
31
е ф :) = л : - ^ = л :- 0 .1 л
:3
+0.2jc
2
-0.7л:-0 .3 = -0.1л
:3
+ 0.2л
:2
+ 0.3x-0.3.
^
к
Пусть л:д = 0 , тогда
х п+\ = <р(хп ) .
Вычисления располагаем в
таблице:
__________
п
х п
У
0
0
-0.3
1
-0.3
-0.3693
2
-0.3693
-0.3785
3
-0.3785
-0.3795
4
-0.3795
-0.3796
5
-0.3796
Ответ:
х
» -0.380.
Метод хорд
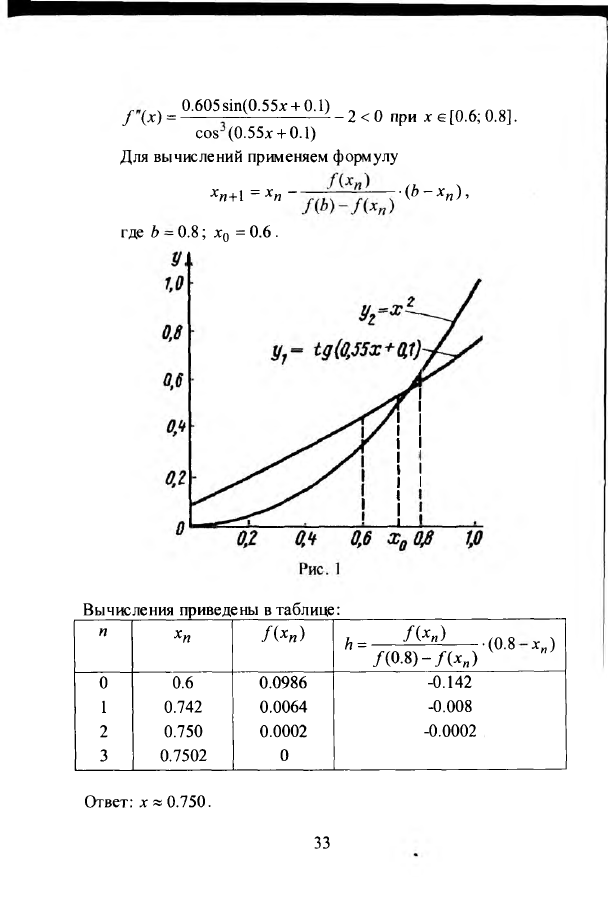
Дано уравнение #(0.55л: + 0.1) = л:2 . Отделим корень
графически. Построим графики функций
у х
=
tg(0.55x
+ 0.1) и
у 2 - х
(рис. 1). Из рисунка видно, что положительный корень
уравнения заключен в промежутке [
0
.
6
;
0
.
8
].
Чтобы уточнить корень методом хорд, определим знаки
функции
f ( x )
= #(0.55л: + 0 .1 )-л
:2
на концах промежутка
[
0
.
6
;
0
.
8
] и знак второй производной в этом промежутке:
/(0 .6 ) = #(0.43) - 0.36 = 0.4586 - 0.36 = 0.0986;
/(0 .8 ) = # (0.54) - 0.64 = 0.5994 - 0.64 = -0.0406;
0.55
^
/
(х)
= ----
-
-------------------
2 х
;
cos (0.55л:+ 0.1)
32
0.605 sin(0.55x + 0.1)
/ (x) = ------- -— ---------------- -
2
<
0
при x e [
0
.
6
;
0
.
8
].
cos (0.55x + 0.1)
Для вычислений применяем формулу
х п
+ 1 =
х п
------- --------------
( Ь - х п ) ,
где
Ъ -
0
.
8
; х
0
=
0.6
.
Вычисления приведены в таблице:
п
х п
Л * л )
h =
f<<Xn)
-(
0.8
х„)
Д
0
.
8
) - / ( х и)
0
0.6
0.0986
-0.142
1
0.742
0.0064
-0.008
2
0.750
0.0002
-
0.0002
3
0.7502
0
Ответ: х * 0.750.
33

Лабораторная работа №9
МЕТОД НЬЮТОНА Н Е Г О МОДИФИКАЦИИ
Задание.
Определить с точностью 10
~6
решения уравнений из
лабораторной
работы
№8
методом
Ньютона,
упрощенным методом Ньютона и методом секущих.
Сравнить число итераций.
Образец выполнения задания
Дано
уравнение
Д х ) = х
3
-0 .2 л
:2
+ 0.5х + 1.5 = 0;
/ '( х ) = Зх
2
- 0.4х + 0.5 .
Составим таблицу знаков функции:_________________________
X
— оо
-1
0
+ 00
/ ( * )
-
-
+
+
Уравнение имеет действительный корень, лежащий в
промежутке [—1;0]. Уточним этот корень методом Ньютона.
Так как / ( —1) < 0 , / ( 0 ) > 0 и /* (х ) < 0 , то за начальное
приближение принимаем хд = -
1
.
Для вычислений применяем формулу
х
= х
/ '( * „ )
Для вычислений используем таблицу:
п
х п
Д * и )
г ы
й =
/ ю
0
-I
-
0.2
;
3.9
-0.051
1
-0.949
-0.0093
3.5814
-0.0026
2
-0.9464
-0.0004
3.5657
-
0.00001
Ответ: х « -0.946.
34
Лабораторная работа №10
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Задание.
Используя методы простой итерации и Ньютона
найти решение системы нелинейных уравнений с
точностью 10 4 . Сравнить число итераций.
№
1
.
№
2
.
№3.
№4.
№5.
№
6
.
№7.
+
-
2
=
0
,
х 2 - 2у =
0
;
yjx + l - у
=
0
,
х 2 + у 2 - 2 у = 0;
(х <
0
).
(х >
0
).
[
jc c o s
(
jc
) —
= 0 ,
j
j
(дс > 0 ) .
[х* + y z -1 = 0;
д
:2
+ у
2
—1
=
0
,
2хе~х - у = 0;
2 х 2 + у 2 - 1 = 0,
х 2 П ~ У = 0
;
( х <
0
).
О > >
0
).
fsin(jc) — =
0
,
2
2
( х > 0 ) .
[xz + y
2 - 1
=
0
;
х 2 + у 2 - 2 у
=
0
,
е ~ х - у = Ъ
(л: < 0).
35