Файл: Audio and Radio Engineering.pdf

9-27

Chapter

9.2

Properties of Magnetic Materials

Beverley R. Gooch

9.2.1

Introduction

The performance of a magnetic tape recorder depends heavily on the properties of the magnetic
materials used to make the recording heads and tapes. Today’s magnetic materials are the product
of sophisticated metallurgy and advanced manufacturing techniques, which in large measure are
responsible for the advancement of the magnetic recording technology.

Magnetic materials are classified as either magnetically hard or magnetically soft. Both types

are used in magnetic tape recorders.

The hard magnetic materials are so-called because of their ability to retain magnetism after

being exposed to a magnetic field. The measure of this property is called remanence.  These
materials may be further characterized by high coercivity and low permeability. Coercivity is the
resistance of the material to being magnetized or demagnetized. Permeability is a measure of the
magnetic conductivity relative to air.

In magnetic recording, hard magnetic materials are used chiefly in the manufacturing of

recording tape and other related media. Some examples are gamma ferric oxide (

γ -ferric oxide),

iron oxide, and chromium dioxide. Hard materials are also used to make permanent magnets for
use in loudspeakers, electric motors, and other applications.

On the other hand, soft magnetic materials such as Alfesil, hot-pressed ferrite, and Permalloy

exhibit low coercivity, low remanence, and relatively high permeability. These materials are used
to make cores for magnetic heads.

Ferromagnetic materials have permeabilities much greater than unity and show a strong mag-

netic effect. Ferromagnetism is exhibited mostly by metallic elements such as iron, cobalt,
nickel, and magnetic metals that are alloys of these elements. With the exception of ferrites [1,
2], most magnetic materials used in tape recorders are ferromagnetic.

Paramagnetic substances have permeabilities that lie between 1.000 and 1.001. These materi-

als do not show hysteresis, and their permeabilities are independent of field strength. Some
examples of paramagnetic materials are sodium, potassium, oxygen, platinum, and ferromag-
netic metals above the Curie temperature [1].

Diamagnetic materials have a relative permeability slightly less than 1. Many of the metals

and most nonmetals are diamagnetic [1].

Magnetic anisotropy is the term applied to magnetic materials that exhibit preferred direc-

tions of magnetization. These preferred and nonpreferred directions are referred to as the easy

Source: Standard Handbook of Audio and Radio Engineering

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

9-28 Audio Recording Systems

and hard axes of magnetization, respectively. The higher the magnetic anisotropy, the harder it is
to change the magnetization away from the preferred direction. In most polycrystalline materials,
the crystals are randomly oriented and are magnetically isotropic. Single crystal ferrites and
magnetic particles used in tape coating are examples of magnetic materials that are anisotropic
[1, 3].

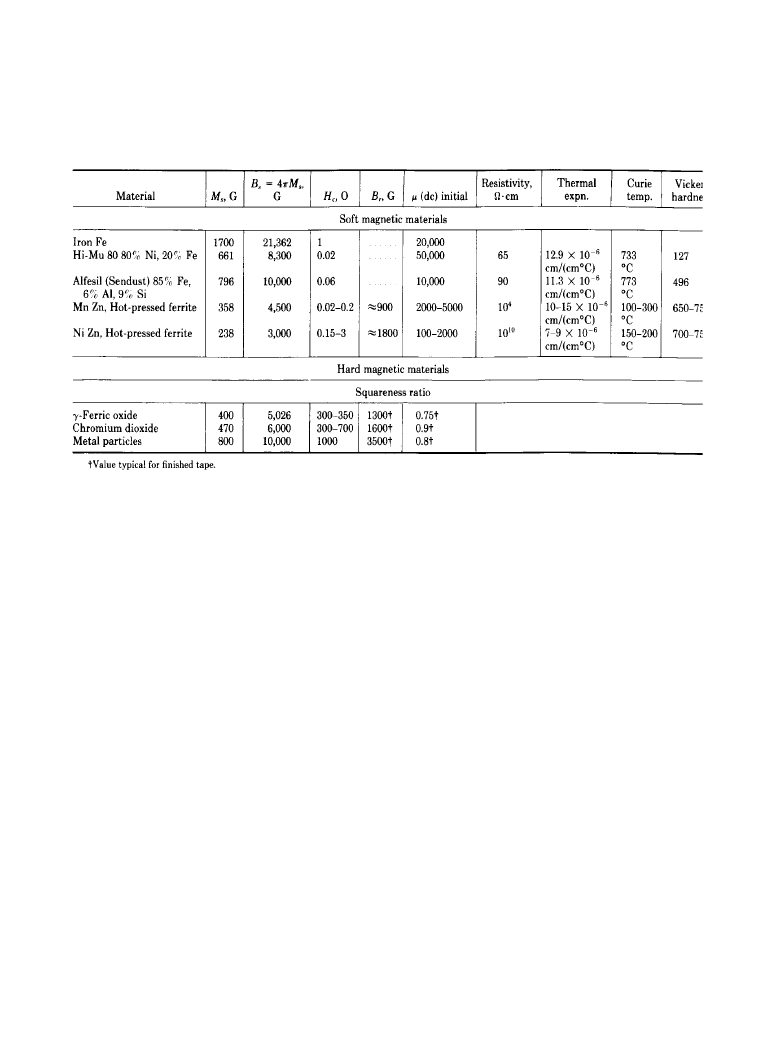
Table 9.2.1 shows properties of materials commonly used in magnetic heads and tapes.

9.2.2

Basic Principles of Magnetism

Magnetism results from two sources: orbital motion of electrons around the nucleus and the spin-
ning of the electrons on their own axes (see Figure 9.2.1). Both the orbital and spin motions con-
tribute to the magnetic moment of the atom, although in most magnetic substances almost all the
magnetic moment is due to the spin motion. As the electron spins on its axis, the charge on its
surface moves in a circular pattern. This moving charge, in turn, produces a current that creates a
magnetic field. This phenomenon occurs in all substances. However, the electrons of the atoms
in nonmagnetic materials occur in pairs with the spins in opposite directions, balancing each
other and rendering the atom magnetically neutral. The atoms can produce the external effect of
a magnet only when the electron spins are unbalanced.

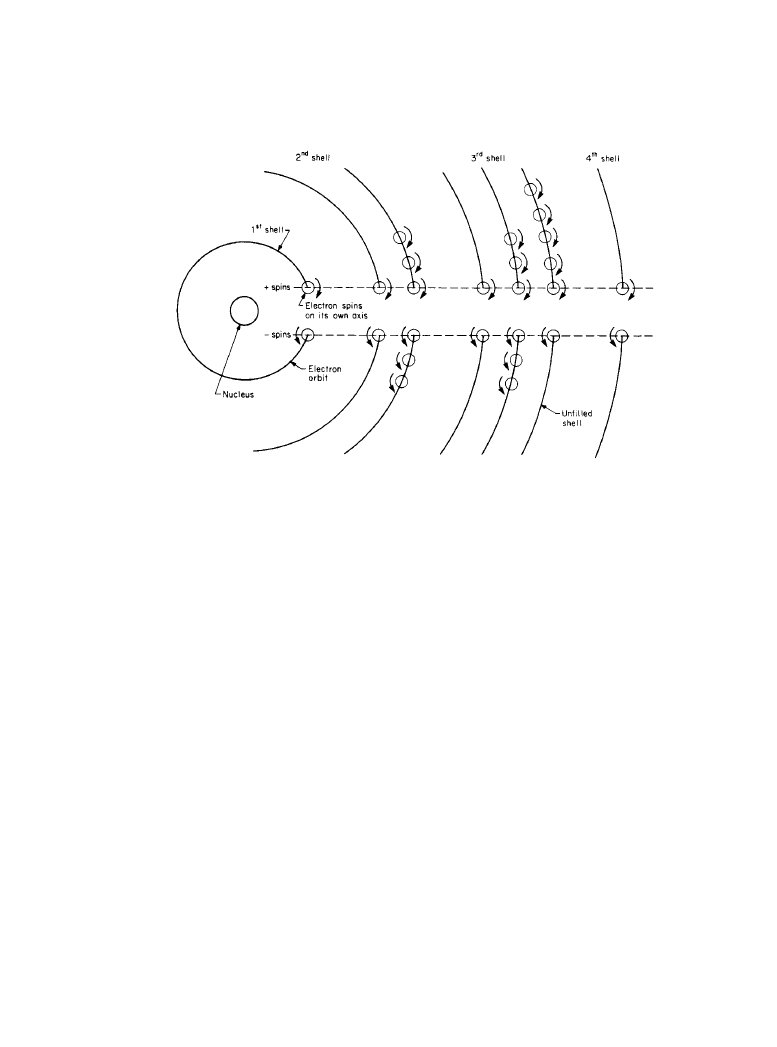
The iron atom, for example, has 26 electrons in rotation around its nucleus (Figure 9.2.1).

These orbiting electrons occur in regions called shells. According to quantum theory, the maxi-
mum number of electrons that can exist in each shell is 2N

2

, where N is the number of the shell.

Starting from the nucleus, the first, second, third, and fourth shells could have a maximum num-

Table 9.2.1 Properties of Soft and Hard Magnetic Materials

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Properties of Magnetic Materials

Properties of Magnetic Materials 9-29

ber of 2, 8, 18, and 32, respectively. The maximum number of electrons in each shell may not be
reached before the next shell begins to form. The iron atom actually has two electrons in the first
shell, the second has eight, the third and fourth shells have fourteen and two, respectively. The
plus and minus signs show the direction of the electron spins. The electron spins in the first, sec-
ond, and fourth shells balance each other, and produce no magnetic effect. It is the third shell that
is of particular interest in the iron atom. In this shell there are five electrons with positive spins
and one with a negative spin, which gives the atom a net magnetic effect.

Thermal agitation energy, even at low temperatures, would prevent the atomic magnets from

being aligned sufficiently to produce a magnetic effect. However, powerful forces hold the elec-
tron spins in tight parallel alignment against the disordering effect of thermal energy. These
forces are called exchange forces.

The parallel alignment of the electron spins, due to the exchange forces, occurs over large

regions containing a great number of atoms. These regions are called domains. Each domain is
magnetized to saturation by the aligned electron spins. Because this magnetization occurs with
no external field applied, it is referred to as spontaneous magnetization. When the magnetic
material is in the demagnetized state, the direction of the magnetization of the saturated domains
is distributed in a random order, bringing the net magnetization of the material to zero. The
domains are separated from each other by partitions called Bloch walls [1, 3]. The domain wall
pattern is determined by the strains within the material and its composition.

In soft magnetic materials the magnetization takes place by the displacement of the domain

walls [1, 3]. The wall movement is not continuous but occurs in discrete steps called Barkhausen

Figure 9.2.1

 Schematic diagram of an iron atom.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Properties of Magnetic Materials

9-30 Audio Recording Systems

steps or jumps  that are related to imperfections or inclusions in the crystalline structure of the
material.

The particles used in magnetic tape coating are so small that Bloch walls do not form. They

behave as single-domain particles that are spontaneously magnetized to saturation. Irreversible
magnetization is achieved only through irreversible rotation of the individual particle magnetiza-
tions [4, 5].

9.2.2a

Curie Point

The Curie point is the temperature at which the thermal agitation energy overcomes the exchange
forces. The spontaneous magnetization disappears and the material is rendered nonmagnetic.
This process is reversible; when the temperature is lowered below the Curie point, the spontane-
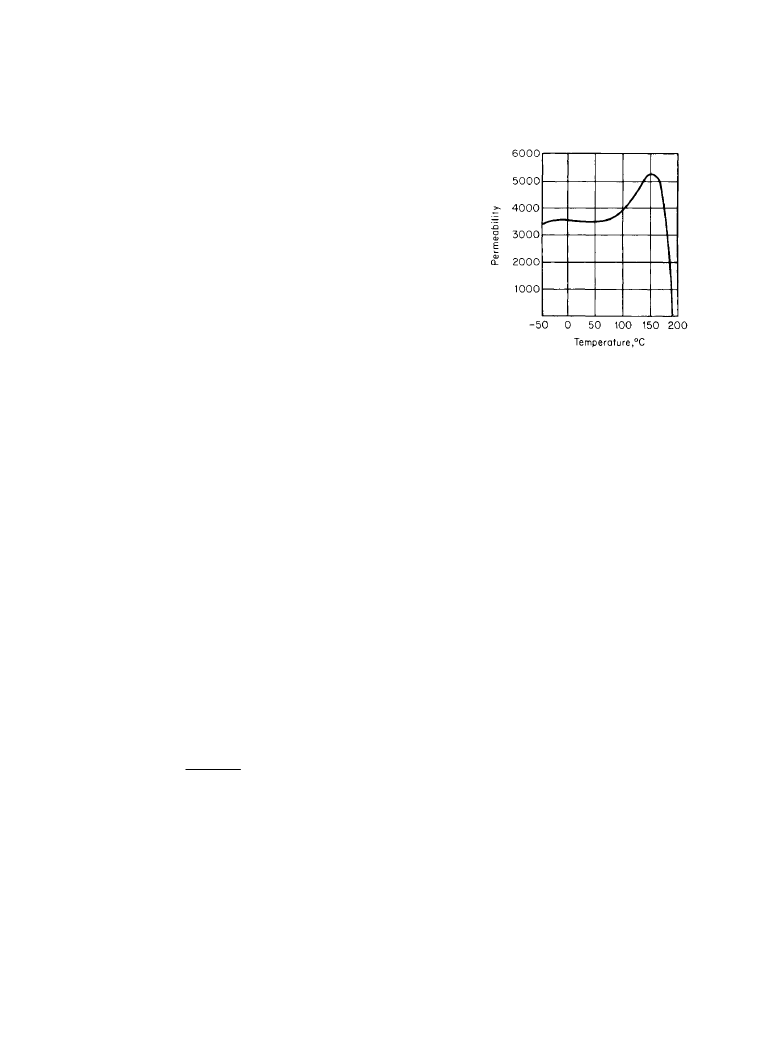
ous magnetization returns and the material is again magnetic. Figure 9.2.2 shows the effect of
temperature on the permeability of a typical ferrite.

9.2.2b

Magnetic Induction

When a current I is connected to a solenoid coil of N turns, a magnetic field H is created that has
direction as well as strength, and is defined by:

(9.2.1)

Where:
H = magnetic field in oersteds
l = length of the solenoid in centimeters
I = current in amperes

As a result of the field H, flux lines are produced in the surrounding space (see Figure 9.2.3).

The flux lines form closed loops that flow from one end of the solenoid coil, into the air, and

0.4

N I

H

l

π

=

Figure 9.2.2

 Effect of temperature on the permeability of

typical ferrite.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Properties of Magnetic Materials

Properties of Magnetic Materials 9-31

reenter the coil at the opposite end. The measure of the intensity or the concentration of the flux
lines per unit area is called the flux density, or the induction B.

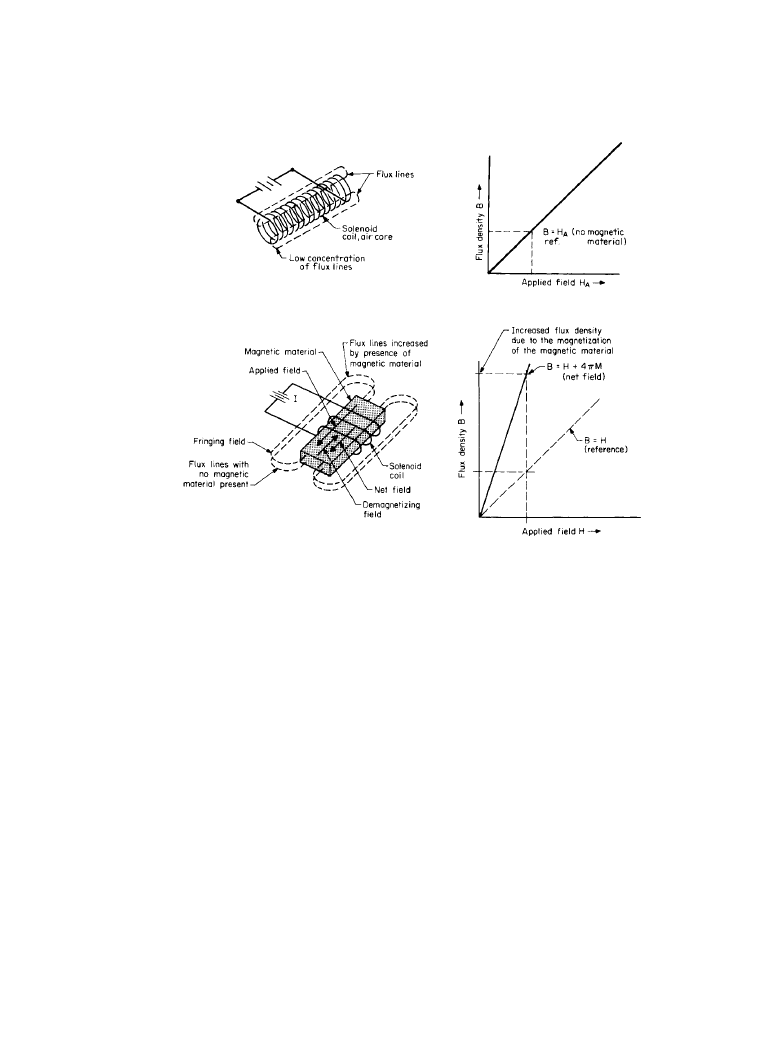
Figure 9.2.3a shows that with no magnetic material present in the solenoid coil the flux den-

sity B is relatively low and is equal to the applied field H. When a piece of magnetic material is
placed in the solenoid coil, the flux density is increased (Figure 9.2.3b). This results from the
magnetic moments of the electron spins aligning themselves with the applied field H, causing
the magnetic material to become a magnet [1, 6]. The sum of the magnetic moments per unit vol-
ume is the magnetization M. The magnetization of a material creates magnetic fields. Inside the
material these fields are called demagnetization fields because they oppose the magnetization.
Outside the material, they are called stray or fringing fields. The net field acting on the material
is the vectorial sum of the demagnetization field and the applied field. The flux density is the net
field plus the magnetization M, that is:

(9.2.2)

where H = net field and M and B are in gauss

4

B

H

M

π

=

+

(

b)

Figure 9.2.3

 Properties of flux increase: (

a) air core, (b) magnetic core material.

(

a)

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Properties of Magnetic Materials