Файл: Audio and Radio Engineering.pdf

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Principles of Sound and Hearing

1-7

Chapter

1.1

The Physical Nature of Sound

Floyd E. Toole

E. A. G. Shaw, G. A. Daigle, M. R. Stinson

1.1.1

Introduction

Sound is a physical disturbance in the medium through which it is propagated. Although the
most common medium is air, sound can travel in any solid, liquid, or gas. In air, sound consists of
localized variations in pressure above and below normal atmospheric pressure (compressions and
rarefactions).

Air pressure rises and falls routinely, as environmental weather systems come and go, or with

changes in altitude. These fluctuation cycles are very slow, and no perceptible sound results,
although it is sometimes evident that the ears are responding in a different way to these infra-
sonic events. At fluctuation frequencies in the range from about 20 cycles per second up to about
20,000 cycles per second the physical phenomenon of sound can be perceived as having pitch or
tonal character. This generally is regarded as the audible or audio-frequency range, and it is the
frequencies in this range that are the concern of this chapter. Frequencies above 20,000 cycles
per second are classified as ultrasonic.

1.1.2

Sound Waves

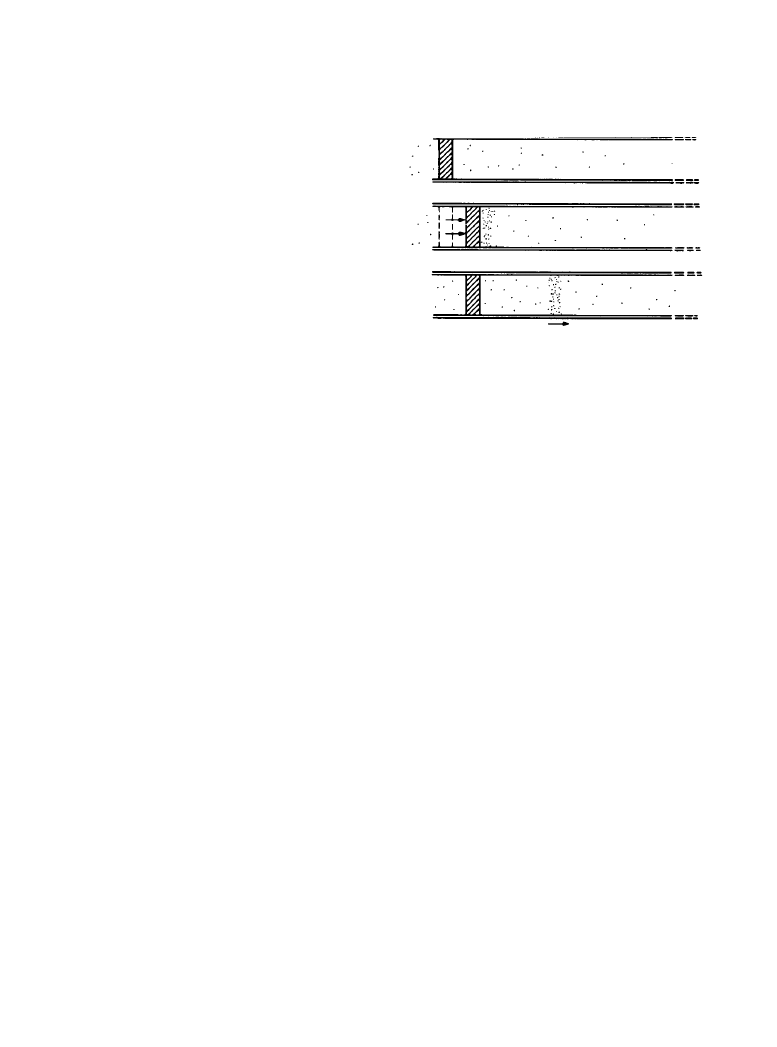
The essence of sound waves is illustrated in Figure 1.1.1, which shows a tube with a piston in one
end. Initially, the air within and outside the tube is all at the prevailing atmospheric pressure.
When the piston moves quickly inward, it compresses the air in contact with its surface. This
energetic compression is rapidly passed on to the adjoining layer of air, and so on, repeatedly. As
it delivers its energy to its neighbor, each layer of air returns to its original uncompressed state. A
longitudinal sound pulse is moving outward through the air in the tube, causing only a passing
disturbance on the way. It is a pulse because there is only an isolated action, and it is longitudinal
because the air movement occurs along the axis of sound propagation. The rate at which the
pulse propagates is the speed of sound. The pressure rise in the compressed air is proportional to
the velocity with which the piston moves, and the perceived loudness of the resulting sound pulse

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

Source: Standard Handbook of Audio and Radio Engineering

1-8 Principles of Sound and Hearing

is related to the incremental amplitude of the pressure wave above the ambient atmospheric pres-
sure.

Percussive or impulsive sounds such as these are common, but most sounds do not cease after

a single impulsive event. Sound waves that are repetitive at a regular rate are called periodic.
Many musical sounds are periodic, and they embrace a very wide range of repetitive patterns.
The simplest of periodic sounds is a pure tone, similar to the sound of a tuning fork or a whistle.
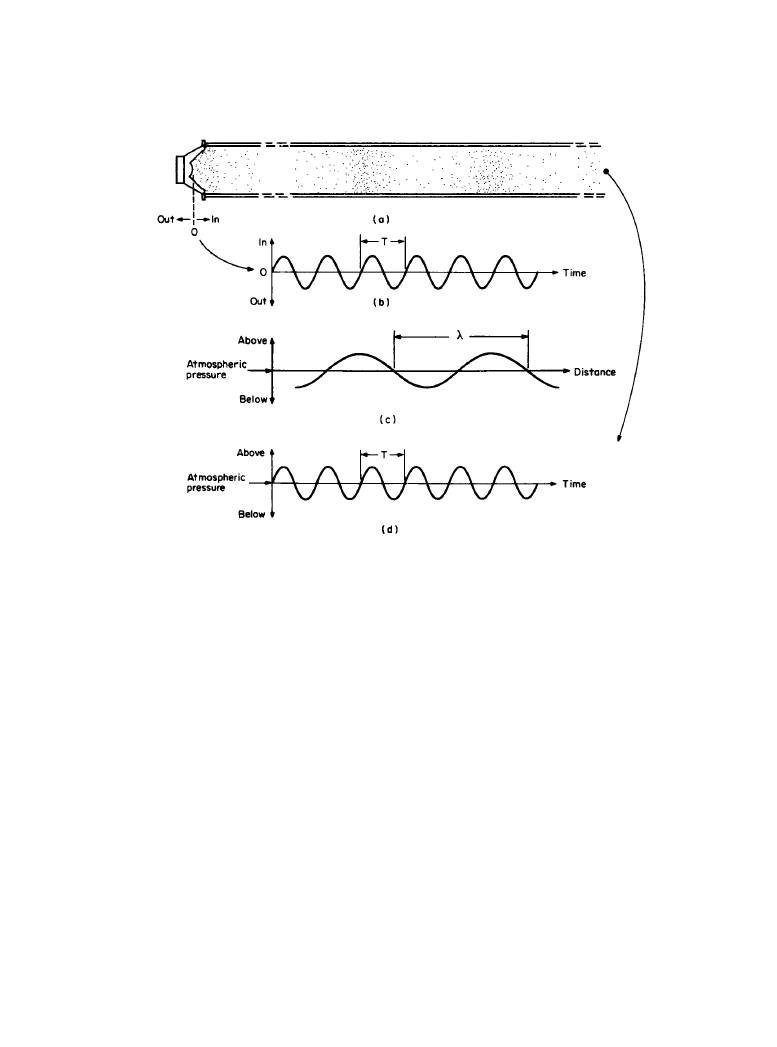
An example is presented when the end of the tube is driven by a loudspeaker reproducing a
recording of such a sound (Figure 1.1.2). The pattern of displacement versus time for the loud-
speaker diaphragm, shown in Figure 1.1.2b, is called a sine wave or sinusoid.

If the first diaphragm movement is inward, the first event in the tube is a pressure compres-

sion, as seen previously. When the diaphragm changes direction, the adjacent layer of air under-
goes a pressure rarefaction. These cyclic compressions and rarefactions are repeated, so that the
sound wave propagating down the tube has a regularly repeated, periodic form. If the air pressure
at all points along the tube were measured at a specific instant, the result would be the graph of
air pressure versus distance shown in Figure 1.1.2c. This reveals a smoothly sinusoidal waveform
with a repetition distance along the tube symbolized by 

λ (lambda), the wavelength of the peri-

odic sound wave.

If a pressure-measuring device were placed at some point in the tube to record the instanta-

neous changes in pressure at that point as a function of time, the result would be as shown in Fig-
ure 1.1.2d. Clearly, the curve has the same shape as the previous one except that the horizontal
axis is time instead of distance. The periodic nature of the waveform is here defined by the time
period T, known simply as the period of the sound wave. The inverse of the period, 1/T, is the fre-
quency of the sound wave, describing the number of repetition cycles per second passing a fixed
point in space. An ear placed in the path of a sound wave corresponding to the musical tone mid-
dle C would be exposed to a frequency of 261.6 cycles per second or, using standard scientific
terminology, a frequency of 261.6 hertz (Hz). The perceived loudness of the tone would depend
on the magnitude of the pressure deviations above and below the ambient air pressure.

The parameters discussed so far are all related by the speed of sound. Given the speed of

sound and the duration of one period, the wavelength can be calculated as follows:

(1.1.1)

λ

cT

=

Figure 1.1.1

 Generation of a longitudinal

sound wave by the rapid movement of a pis-
ton in the end of a tube, showing the propa-
gation of the wave pulse at the speed of
sound down the length of the tube.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

The Physical Nature of Sound

The Physical Nature of Sound 1-9

where:
λ = wavelength
c = speed of sound
T = period

By knowing that the frequency f = l/T, the following useful equation and its variations can be
derived:

(1.1.2)

The speed of sound in air at a room temperature of 22°C (72°F) is 345 m/s (1131 ft/s). At any

other ambient temperature, the speed of sound in air is given by the following approximate rela-
tionships [1, 2]:

λ

c

f

--

=          

f

c

λ

---

=

     c

f

λ

=

Figure 1.1.2

 Characteristics of sound waves: (

a) A periodic sound wave, a sinusoid in this exam-

ple, is generated by a loudspeaker placed at the end of a tube. (

b) Waveform showing the move-

ment of the loudspeaker diaphragm as a function of time: displacement versus time. (

c) Waveform

showing the instantaneous distribution of pressure along a section of the tube: pressure versus
distance. (

d) Waveform showing the pressure variation as a function of time at some point along

the tube: pressure versus time.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

The Physical Nature of Sound

1-10 Principles of Sound and Hearing

(1.1.3)

or

(1.1.4)

where t = ambient temperature.

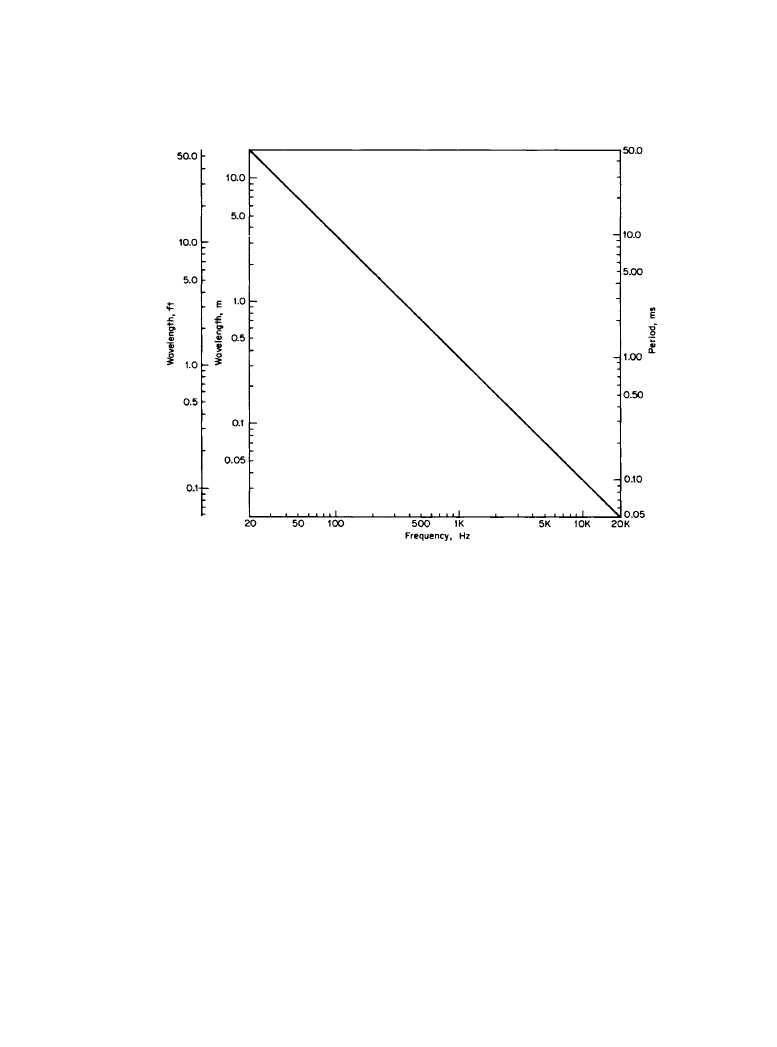
The relationships between the frequency of a sound wave and its wavelength are essential to

understanding many of the fundamental properties of sound and hearing. The graph of Figure
1.1.3 is a useful quick reference illustrating the large ranges of distance and time embraced by
audible sounds. For example, the tone middle C with a frequency of 261.6 Hz has a wavelength
of 1.3 m (4.3 ft) in air at 20°C. In contrast, an organ pedal note at Cl, 32.7 Hz, has a wavelength
of 10.5 m (34.5 ft), and the third-harmonic overtone of C8, at 12,558 Hz, has a wavelength of
27.5 mm (1.1 in). The corresponding periods are, respectively, 3.8 ms, 30.6 ms, and 0.08 ms. The
contrasts in these dimensions are remarkable, and they result in some interesting and trouble-
some effects in the realms of perception and audio engineering. For the discussions that follow it
is often more helpful to think in terms of wavelengths rather than in frequencies.

c m/s

(

)

331.29

0.607t

° C

(

)

+

=

c m/s

(

)

1051.5

1.106t

° F

(

)

+

=

Figure 1.1.3

 Relationships between wavelength, period, and frequency for sound waves in air.

Downloaded from Digital Engineering Library @ McGraw-Hill (www.digitalengineeringlibrary.com)

Copyright © 2004 The McGraw-Hill Companies. All rights reserved.

Any use is subject to the Terms of Use as given at the website.

The Physical Nature of Sound