ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 256
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое занятие №11
«Кривые второго порядка»
Цель: закрепить знание определения окружности, эллипса, гиперболы и параболы, фокуса, осей, асимптот и эксцентриситета; научиться находить элементы кривых 2-го порядка, составлять уравнения кривых второго порядка и строить в координатной плоскости.
Теоретическая часть
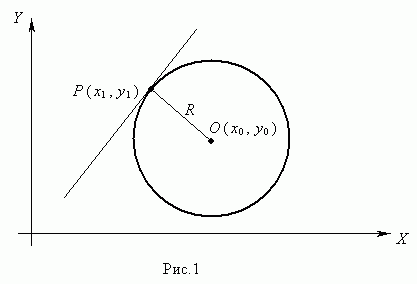 Окружностью (рис.)называется геометрическое место точек, равноудалённых от данной точки О, называемой центром окружности, на расстояние R. Число R> 0 называется радиусом окружности.
Окружностью (рис.)называется геометрическое место точек, равноудалённых от данной точки О, называемой центром окружности, на расстояние R. Число R> 0 называется радиусом окружности. Уравнение окружности имеет вид
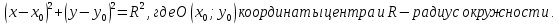
Например:
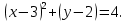
Переход от последнего уравнения к общему виду. Для удобства заменим
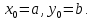
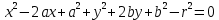
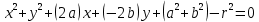
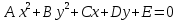 - общее уравнение окружности
- общее уравнение окружностиЕсли центр окружности совпадает с началом координат, то уравнение окружности упрощается:
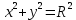 . Например:
. Например: 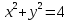 .
.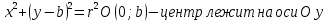
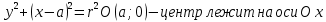
Пусть Р ( х1 , у 1 ) – точка окружности ( рис.1 ), тогда уравнение касательной к окружности в данной точке имеет вид:
( х1 – х0) ( х – х0 ) + ( у1 – у 0 ) ( у – у 0 ) = R 2 .
Условие касания прямойy = mx + kи окружности х2 + у 2 = R 2 :
k 2 / (1 +m2 )=R 2 .
Пример 1.Доказать, что уравнение х2+ у2 + 8х - 4у -5 = 0 является уравнением окружности. Найти её центр и радиус.
Решение: Разделив уравнение на 2 и сгруппировав члены уравнения, получим х2- 4х +у2 +
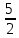 у = 2. Дополним полученные выражения относительно переменных до полного квадрата двучлена
у = 2. Дополним полученные выражения относительно переменных до полного квадрата двучлена (х2-
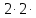 х + 4) - 4 +(у2 +
х + 4) - 4 +(у2 +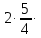 у +
у +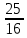 ) -
) - 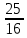 = 2
= 2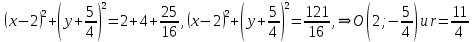 .
.Ответ:
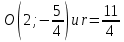 .
.Пример 2. Составить уравнение окружности, проходящей через точки А(7;7) и В(-2; 4), если ее центр лежит на прямой 2х – y – 2 = 0.
Решение: Уравнение окружности:
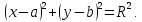 Так как точки А и В лежат на данной окружности, то координаты этих точек будут удовлетворять уравнениям:
Так как точки А и В лежат на данной окружности, то координаты этих точек будут удовлетворять уравнениям: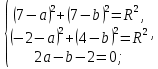 центр окружности по условию лежит на прямой.
центр окружности по условию лежит на прямой.Раскроем скобки
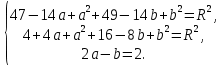 Вычтем из первого уравнения второе
Вычтем из первого уравнения второе 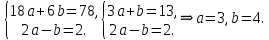 Полученное подставим в любое уравнение и найдём R=5. Искомое уравнение имеет вид
Полученное подставим в любое уравнение и найдём R=5. Искомое уравнение имеет вид 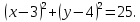
Ответ:
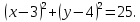
Эллипсом (рис.) называется множество точек плоскости, сумма расстояний которых до двух данных точек F1 и F2, называемых фокусами эллипса, есть величина постоянная, равная 2a.
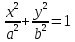 - каноническое уравнение эллипса.
- каноническое уравнение эллипса.Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a>b фокусы эллипса лежат на оси ОХ, при a<bфокусы эллипса лежат на оси ОY, а приa = b эллипс становится окружностью(фокусы эллипса в этом случае совпадают с центром окружности). Таким образом, окружность есть частный случай эллипса
.
-
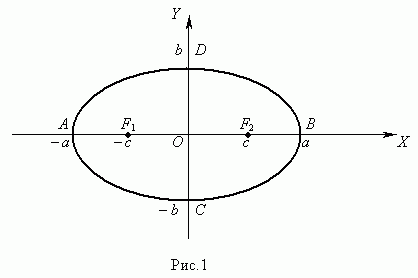
Отрезок F1F2 = 2с, где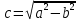 , называетсяфокусным расстоянием.
, называетсяфокусным расстоянием. -
Отрезок AB = 2a называется большой осью эллипса, а отрезок CD = 2b – малой осью эллипса.
-
 Число e = c / a , e< 1 называется эксцентриситетом эллипса – мера сжатости эллипса. Форма эллипса зависит от его эксцентриситета (при e = 1 и b = 0 эллипс переходит в радиус F1F2 т.е. в уравнение окружности). Из этого следует, что окружность это частный случай эллипса, у которого фокусы слились в одну точку и совпали с его центром.
Число e = c / a , e< 1 называется эксцентриситетом эллипса – мера сжатости эллипса. Форма эллипса зависит от его эксцентриситета (при e = 1 и b = 0 эллипс переходит в радиус F1F2 т.е. в уравнение окружности). Из этого следует, что окружность это частный случай эллипса, у которого фокусы слились в одну точку и совпали с его центром.
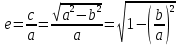
При изменении e от 0 до 1, эллипс будет из окружности, постепенно, сжимаясь, трансформироваться во всё более и более вытянутую кривую пока не перейдёт в отрезок прямой F1F2.
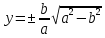 - данное уравнение служит для определения формы эллипса.
- данное уравнение служит для определения формы эллипса.Аналогично
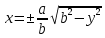 т.к. эллипс симметричен.
т.к. эллипс симметричен. Достаточно рассмотреть его часть в 1 четверти и тогда y> 0 и х > 0, можно построить график функций
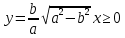
-
Отрезок прямой соединяющий две точки эллипса называется хордой.
Оси симметрии – просто Ось эллипса.
Точка пересечения – центр.
-
Точки в которых эллипс пересекает оси называются вершинами. -
Осями называют также отрезки B1B = 2b, A1A = 2a
Фокальная ось – ось на которой расположены фокусы.
Если
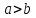 , то величина
, то величина 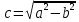 - величина действительная и фокальной осью будет 2a.
- величина действительная и фокальной осью будет 2a.Если
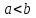 , то величина
, то величина 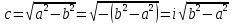 с – мнимая величина. Фокусы будут на оси ординат, фокальной осью будет 2b.
с – мнимая величина. Фокусы будут на оси ординат, фокальной осью будет 2b.Пусть Р(х1, у1) – точка эллипса, тогда уравнение касательной к эллипсу в данной
точке имеет вид:
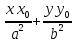 =1.
=1.Условие касания прямой
y = mx + k и эллипса х2/a2 + у 2 / b 2 =1 : k 2 =m2 a2+b 2
Пример 3. Найти каноническое уравнение эллипса, зная его большую полуось а =5 и эксцентриситет е = 0,6.
Решение: Зная, что e
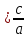 , найдем с = 0,6
, найдем с = 0,6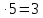 . Но тогда квадрат малой полуоси эллипса
. Но тогда квадрат малой полуоси эллипса 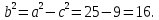 Каноническое равнение эллипса имеет вид
Каноническое равнение эллипса имеет вид 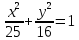 .
.Ответ:
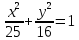 .
.Пример 4. Составить каноническое уравнение эллипса, проходящего через точки М
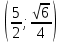 и N
и N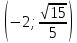 .
.Решение: Пусть
 искомое уравнение эллипса, координаты данных точек должны ему удовлетворять, т.е.
искомое уравнение эллипса, координаты данных точек должны ему удовлетворять, т.е. 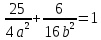 и
и 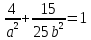 , или
, или 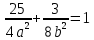 и
и 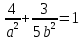 .
.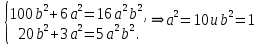 . Уравнение эллипса имеет вид
. Уравнение эллипса имеет вид 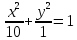
Ответ:
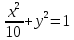 .
.Пример 5. Составить уравнение касательной к эллипсу
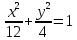 в точке (3; 1).
в точке (3; 1).Решение: Так как уравнение касательной к эллипсу
 имеет вид
имеет вид  =1, то искомое уравнение касательной к данной кривой будет:
=1, то искомое уравнение касательной к данной кривой будет: 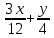 =1,
=1, 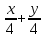 =1.
=1.Ответ: x + y – 4 = 0.
Пример 6. Доказать, что уравнение64х2+100у2-6400=0 является уравнением эллипса. Найдите координаты и фокальное расстояние.
Решение: Разделив обе части уравнения на 6400, получим
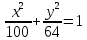
- это каноническое уравнение эллипса. Из равенства
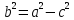 , следует, что
, следует, что 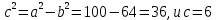 . Фокусы эллипса будут находиться в точках F1(-6; 0) и F2(6; 0). Фокальное расстояние 2с =12.
. Фокусы эллипса будут находиться в точках F1(-6; 0) и F2(6; 0). Фокальное расстояние 2с =12.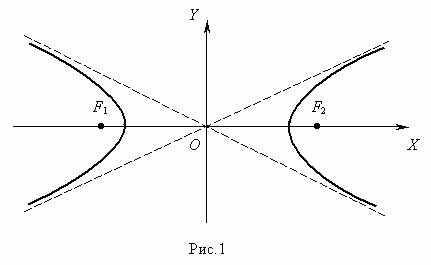 Ответ: F2(-6; 0) и F1(6; 0), 2с =12.
Ответ: F2(-6; 0) и F1(6; 0), 2с =12.Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек F1 и F2, называемыхфокусами гиперболы, есть величина постоянная, равная 2a.
Каноническое уравнение гиперболы.
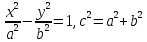 .
. Гипербола
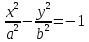 называется сопряженной с гиперболой
называется сопряженной с гиперболой 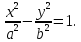
Числа a и b называются соответственно вещественной и мнимыми полуосями гиперболы.
-
Ось гиперболы – прямая соединяющая её фокусы. -
Расстояние от начала координат до одного из фокусов гиперболы, называют фокусами расстояний гиперболы. -
Расстояние от начала координат до одной из вершин гиперболы называют большой или вещественной полуосью гиперболы a,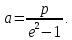
-
Расстояние от вершины гиперболы до асимптоты в доле направления параллельное оси ординат называется малой или мнимой полуосью гиперболы b,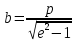 .
. -
y =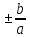 x – прямые являются асимптотами гиперболы.
x – прямые являются асимптотами гиперболы. -
Отношение фокусного расстояния к большой полуоси гиперболы называется эксцентриситетом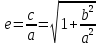 ,
,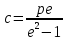 . Эксцентриситет гиперболы всегда больше единицы.
. Эксцентриситет гиперболы всегда больше единицы. -
Расстояние от фокуса до гиперболы вдоль прямой параллельной Оси ординат называется фокальным параметром р,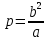 .
. -
Парацентрическое расстояние (r.p.) – расстояние от фокуса до ближайшей вершины гиперболы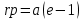 (в задачах связанных с движением)
(в задачах связанных с движением) -
Предельным параметром называют расстояние от фокуса до одной из асимптот гиперболы. Предельный параметр равен малой полуоси гиперболы.