ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 258
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пусть Р(х1, у1) – точка гиперболы, тогда уравнение касательной к гиперболе в данной
точке имеет вид:
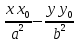 =1.
=1.Условие касания прямой y = mx + k и гиперболы х2/a2 - у 2 / b 2 =1 :
k 2 =m2 a2+b 2
Пример 1. Написать каноническое уравнение гиперболы, проходящей через точку М(
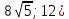 , если фокальное расстояние гиперболы равно 20.
, если фокальное расстояние гиперболы равно 20.Решение: По условию 2с = 20, с =10. Запишем каноническое уравнение гиперболы
 По условию точка М принадлежит гиперболе, т.е.
По условию точка М принадлежит гиперболе, т.е. 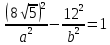 и второе уравнение для нахождения a и b:
и второе уравнение для нахождения a и b: 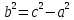 = 100 -
= 100 -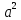 .
.Решим систему уравнений
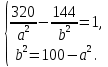 Решая систему относительно aиb(a>0, b>0), найдем
Решая систему относительно aиb(a>0, b>0), найдем 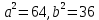 . Искомым уравнением будет
. Искомым уравнением будет 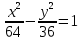 .
.Ответ:
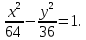
Пример 2. Составить каноническое уравнение гиперболы, зная, что расстояние между ее фокусами равно 26, а эксцентриситет равен 13/12.
Решение: По условию 2с=26, с=13 и e =c/a=13/12. Следовательно, большая полуось гиперболы a =
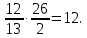 По формуле
По формуле 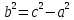 = 169 -144=25,
= 169 -144=25, 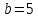 . Уравнение гиперболы имеет вид
. Уравнение гиперболы имеет вид 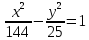 .
.Ответ:
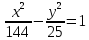 .
.Пример 3. Построить гиперболу 16х2 - 9у2 = 144. Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнение асимптот.
Решение: Разделив обе части уравнения на 144, получим
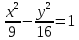
.
а) полуоси гиперболы a=
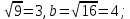
б) координаты фокусов:
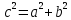 , c=
, c= 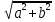 =5. Фокусы F2(-5; 0) и F1 (5; 0);
=5. Фокусы F2(-5; 0) и F1 (5; 0);в) эксцентриситет
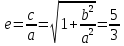 ;
;г) уравнение асимптот y =
 x =
x = 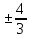 x .
x .Ответ:
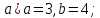 б) F2(-5; 0) и F1 (5; 0); в)
б) F2(-5; 0) и F1 (5; 0); в) 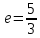 ; г) y =
; г) y = 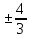 x .
x .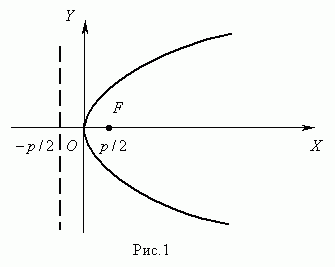 Параболой называется множество точек плоскости, равноудалённых от заданной точкиF, называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.
Параболой называется множество точек плоскости, равноудалённых от заданной точкиF, называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.Каноническое уравнение параболы (рис.1):
y 2 = 2px , р>0.
Число р параметр параболы. Начало координат О(0;0) – вершина параболы, а ось ОХ является осью симметрии параболы. Точка F(p/2; 0) – фокус параболы, х = -р/2 директриса параболы.
Пусть Р(х1, у1) – точка параболы, тогда уравнение касательной к параболев данной точке имеет вид: у1y = p(x+ х1) .
Условие касания прямойy = mx + kи параболы y 2 = 2px: 2mk =p .
Пример 4. Составить уравнение параболы, симметричной относительно оси Ох, с вершиной в начале координат, если длина некоторой хорды этой параболы, перпендикулярной оси Ох равна 16, а расстояние этой хорды от вершины равно 6.
Решение: Так как известны длина хорды и расстояние ее от вершины, то, следовательно, известны координаты конца этой хорды – точки М, лежащей на параболе. Уравнение параболы имеет вид y 2 = 2px; полагая в нем х = 6 и у = 8, находим 82=2р
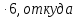
2
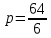 =
= 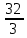 . Итак, уравнение параболы имеет вид y 2 =
. Итак, уравнение параболы имеет вид y 2 =
 x, F(8/3;0)
x, F(8/3;0)Ответ: y 2 =
 x.
x.Пример 5. Написать уравнение касательной к параболе y 2 = 8x, параллельной прямой
2х + 2у – 3 = 0.
Решение: Уравнение касательной к параболеy 2 = 2pxв точке Р(х1,у1) имеет вид
у1y = p(x+ х1).
Сравнивая с уравнениемy 2 = 8x, получим 2р=8, р=4. Тогда уравнение касательной имеет вид у1y = 4(x+ х1) или вид у1y = 4x+4 х1. Так как касательная параллельна прямой 2х + 2у – 3 = 0, то их угловые коэффициенты равны у = - х +
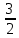 , т.е. k = -1
, т.е. k = -1Э
 ллипс
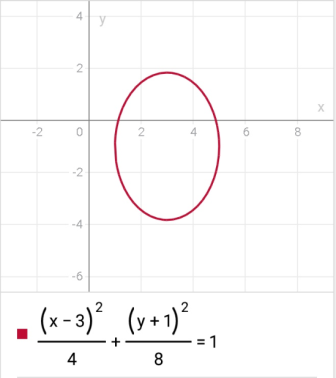
ллипсПример 6. Построить кривую второго порядка по уравнению
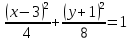 .
.Решение: Из уравнение узнаём, что центр окружности в точке
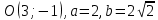 . Так как b>a, то окружность вытянута по оси Оу.
. Так как b>a, то окружность вытянута по оси Оу.Основные характеристики:
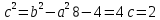
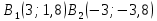
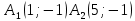
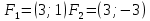
Гипербола
П
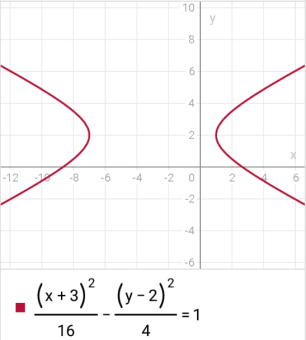 ример 7. Определить вид линии и дать ей основные характеристики, а так же построить
ример 7. Определить вид линии и дать ей основные характеристики, а так же построить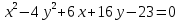 :
:Выделим полный квадрат:
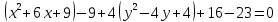
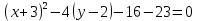
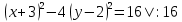
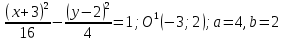 – гипербола
– гипербола Парабола
Пример 8. Построить кривую второго порядка по уравнению
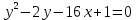 и
и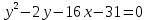 .
.Р
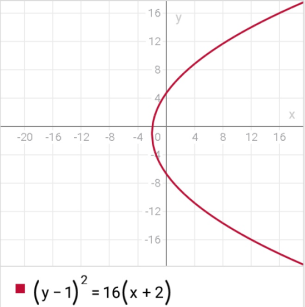 ешение: Прировняем уравнения.
ешение: Прировняем уравнения. 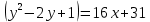
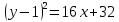
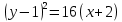
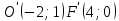
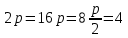
Практическая часть
Задание 1: Составить канонические уравнения: эллипса, гиперболы, параболы
(А, В – точки, лежащие на кривой, F – фокус, а – большая (действительная полуось), b – малая (мнимая) полуось,
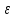 – эксцентриситет,
– эксцентриситет, 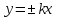 – уравнения асимптот гиперболы, D – директриса кривой, 2с – фокусное расстояние).
– уравнения асимптот гиперболы, D – директриса кривой, 2с – фокусное расстояние).| Вари ант |
|
|
|
| | b=15, F=(-10;0) | a=13, 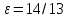 | D: x=-4 |
| | b=2, F=(4 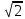 ;0) ;0) | a=7, 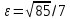 | D: x=5 |
| | A(3;0), B(2; 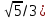 | k=3/4, 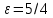 | D: y=-2 |
| | A(-5;0), 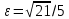 | A( 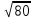 ;3), B(4 ;3), B(4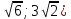 | D: y=1 |
| | 2a=22, 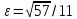 | k=2/3, 2c=10 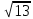 | A(27;9), Ось симметрии Ох |
| | b= 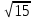 , , 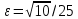 | k=3/4, 2a=16 | A(4;-8), Ось симметрии Ох |
| | a=4, F=(3;0) | b= 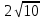 , ,  F(-11; 0) F(-11; 0) | D: x=-2 |
| | b=4, F=(9;0) | a=5, 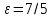 | D: x=6 |
| | A(0; 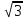 ), B( ), B(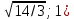 | k= 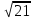 /10, /10, 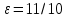 | D: y=-4 |
| | A(8;0), 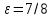 | A( 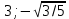 ), B( ), B(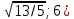 | D: y=4 |
| | 2a=24, 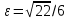 | k= 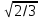 , 2c=10 , 2c=10 | A(-7;-7), Ось симметрии Ох |
| | b=2, 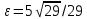 | k=12/13, 2a=26 | A(-5;15), Ось симметрии Ох |
| | a=6, F=(-4;0) | b= 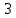 , ,  F(7; 0) F(7; 0) | D: x=-7 |
| | b=7, F=(5;0) | a=11, 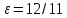 | D: x=10 |
| | A(- 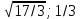 ), B( ), B(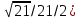 | k=1/2, 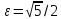 | D: y=-1 |
Задание 2: Упростить уравнение кривой, установить её вид и построить в системе координат.
| Вариант | Уравнение кривой | Вариант | Уравнение кривой |
| 1. | 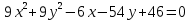 | 9. | 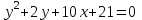 |
| 2. | 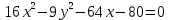 | 10. | 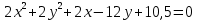 |
| 3. | 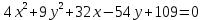 | 11. | 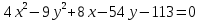 |
| 4. | 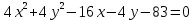 | 12. | 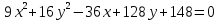 |
| 5. | 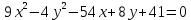 | 13. | 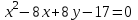 |
| 6. | 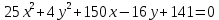 | 14. | 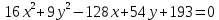 |
| 7. | 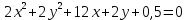 | 15. | 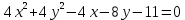 |
| 8. | 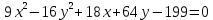 | | |
Контрольные вопросы:
-
Запишите общее уравнение второй степени с двумя переменными. Чем отличается уравнение окружности от него? -
Какие прямые называют директрисами эллипса? -
Запишите уравнение касательной к эллипсу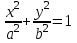 в точке
в точке 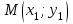 .
.