Файл: Лабораторная работа 1 по дисциплине Статистические методы обработки сигналов аппроксимация экспериментальных данных.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 59
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Чувашский государственный университет им. И.Н.Ульянова»
Лабораторная работа №1
по дисциплине
«Статистические методы обработки сигналов»
АППРОКСИМАЦИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
Вариант 10
Выполнил: студент группы ЗРЭА 22-17п Сармосов М.
Проверил: Тобоев В.А.
Чебоксары 2020
Цель работы: для таблично заданной функции найти параметры следующих
аппроксимирующих функций: линейной, степенной, полиномиальной
и экспоненциальной; построить на одном рисунке исходные данные и графики
аппроксимирующих функций.
Основные теоретические положения
Аппроксимация экспериментальных данных
Аппроксимацией называется подбор аналитической формулы y=f(x) для установленной из опыта функциональной зависимости y=φ(x)
Аппроксимируемая функция у может зависеть от одной или от нескольких переменных. Рассмотрим оба случая.
Основная задача аппроксимации – построение приближенной
(аппроксимирующей) функции y=φ(x) наиболее близко проходящей около экспериментально полученных точек (
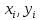), i=0,...,n -1или заданной непрерывной функции y= f (x) . В общем смысле термином «аппроксимация» называют замену одних математических объектов другими, например, сложных функций более простой функцией или набором простых функций, в том или ином смысле близкими к исходным. Для количественной характеристики близости вводится соответствующая мера расстояния, определяемая через разности. При этом весьма желательно, чтобы аппроксимация была как можно более точной и вычислялась за малое время. В простейшем случае задача аппроксимации экспериментальных данных выглядит следующим образом: через заданные точки на плоскости (x, y) или вблизи этих точек провести кривую y
=φ(x) , которая наилучшим образом воспроизводила бы график исходной экспериментальной закономерности, но в то же время была бы нечувствительна к случайным отклонениям измеряемой величины (рис. 3.1).
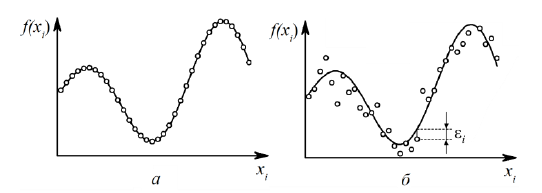
Рис. 3.1. Иллюстрация задачи аппроксимации: а - аппроксимирующая
кривая проходит через заданные точки; б - приближенное описание
экспериментальной зависимости (точки не ложатся в точности на
кривую)
Принято рассматривать эту задачу в двух несколько различных широко распространенных постановках. В первом случае зависимость между величинами x и y задается заранее известной функцией y=φ(x,
,
,....,
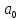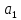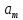) точностью до значений параметров 
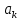(k=0,1,...,m). Задача состоит в том, чтобы как можно точнее оценить эти параметры. Важно отметить, что параметры аппроксимации не могут быть непосредственно найдены из эксперимента.Во второй постановке требуется подобрать функцию y=φ(x,
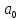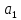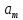, ,...., ) соответствующую наилучшему приближению к фактической экспериментальной зависимости y=f (
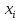), i=0,...,n-1. В этом случае непрерывную функцию φ(x) для аппроксимации дискретной зависимости y=f 
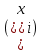выбирают из условия наилучшего квадратичного приближения (стандартный метод наименьших квадратов)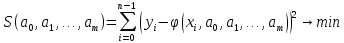
Задачу на поиск минимума
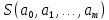можно свести к задаче поиска корня системы уравнений с неизвестными параметрами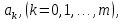 
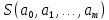
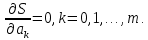
Подстановка (3.1) в (3.2) приведет к системе (m+1) алгебраических уравнений (3.3) относительно неизвестных параметров.
Решая эту систему уравнений, найдем значения параметров
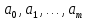и, следовательно, искомую аппроксимирующую функцию 
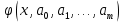, удовлетворяющую сформулированным выше требованиям.Основное преимущество рассмотрения матрицы Грамма состоит в том, что для нахождения решения системы (3.5) необходимо сосчитать только элементы первой строки и двух последних столбцов: остальные элементы заполняются сдвигом предшествующей строки (за исключением двух последних столбцов) на одну позицию влево. А в случае ортогональности базисных функций
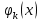
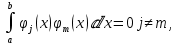
все недиагональные элементы матрицы Грамма равны нулю, что увеличивает точность вычисления параметров. Хорошо известными системами ортогональных базисных функций являются полиномы Лежандра тригонометрические ряды Фурье, вейвлет-функции.
Аппроксимация экспериментальных данных осуществляется путем построения их графика (х – отвлеченные величины) или точечного графика (х – имеет конкретные значения) с последующим подбором подходящей аппроксимирующей функции (линии тренда). Возможны следующие варианты функций:
1. Линейная: у=ах+b. Обычно применяется в простейших случаях, когда экспериментальные данные возрастают или убывают с постоянной скоростью.
2. Полиномиальная: у=а0+а1*х1+a2*х2+...+ аn*хn до шестого порядка включительно (n ≤ 6), аi – константы. Используется для описания экспериментальных данных, попеременно возрастающих и убывающих. Степень полинома определяется количеством экстремумов (максимумов или минимумов) кривой. Полином второй степени может описать только один максимум или минимум, полином третьей степени может иметь один или два экстремума, четвертой степени – не более трех экстремумов и т. д.
3. Логарифмическая: у = а lnx + b, где а и b – константы, ln – функция натурального логарифма. Функция применяется для описания экспериментальных данных, которые вначале быстро растут или убывают, а затем постепенно стабилизируются.
4. Степенная: у=bxa , где а и b – константы. Аппроксимация степенной функцией используется для экспериментальных данных с постоянно увеличивающейся (или убывающей) скоростью роста. Данные не должны иметь нулевых или отрицательных значений.
5. Экспоненциальная: у=bеax, где а и b – константы, е – основание натурального логарифма. Применяется для описания экспериментальных данных, которые быстро растут или убывают, а затем постепенно стабилизируются. Часто ее использование вытекает из теоретических соображений. Степень близости аппроксимации экспериментальных данных выбранной функцией оценивается коэффициентом детерминации (R2). Таким образом, если есть несколько подходящих вариантов типов аппроксимирующих функций, можно выбрать функцию с большим коэффициентом детерминации (стремящимся к 1).
Коэффициент достоверности аппроксимации это значение которое характеризует точность аппроксимации, т. е. показывает на сколько точно теоретическое распределение описывает реальное распределение.
Коэффициент достоверности аппроксимации R2 показывает степень соответствия трендовой модели исходным данным. Его значение может лежать в диапазоне от 0 до 1. Чем ближе R2 к 1, тем точнее модель описывает имеющиеся данные.
Критерий Фишера используется для оценки значимости модели в целом.
Для оценки используется уравнение следующего вида:
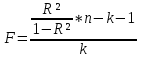
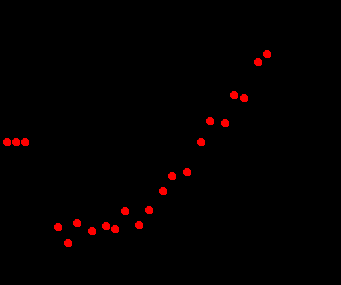
Вычисления в среде Mathcad
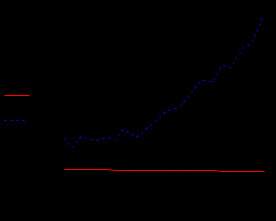
Л и н е й н а я а п п р о к с и м а ц и я
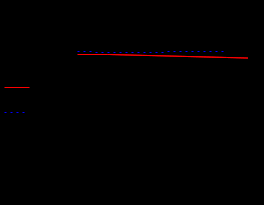
Полиноминальная апроксимация
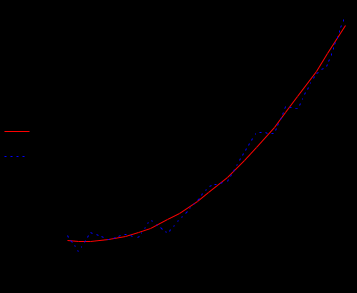
Степенная аппроксимация
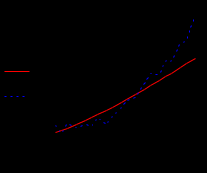
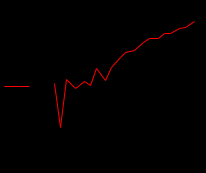
Э к с п о н е н ц а л ь н а я а п п р о к с и м а ц и я
