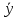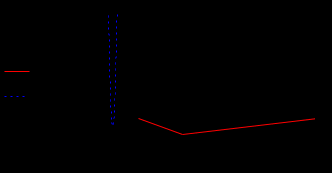
Определение наилучшей аппроксимации

1. 
   Линейная аппроксимация:
   

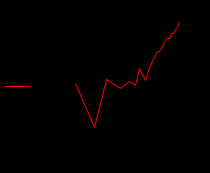
2)Полиноминальная аппроксимация



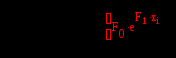
3)Экспоненциальная аппроксимация



4)Степенная аппроксимация

---

---

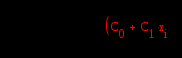
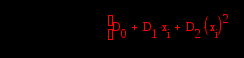
Вывод

Эта лабораторная работа имеет направление на оценку статистических характеристик случайных данных. В данном случае имеется выборка из ста элементов, которую я проверяю на точечное и интервальное оценивание параметров распределения, а также на установление закона распределения по моим данным или опровержение закона распределения.

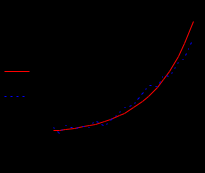
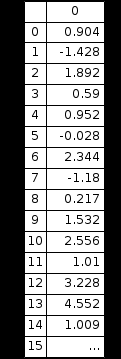
Сначала я строю гистограмму для выборки из нормального распределения нахожу. Для построения гистограммы нужно задать число столбцов(k) (которое в моем случае будет равно 10), дальше требуется найти максимальное и минимальное значения моей выборки, чтобы впоследствии найти длину интервалов группировки. Потом формирую вектор (VJ), компоненты которого являются концами интервалов группировки. Затем вычисляю высоту прямоугольника на j-ом интервале группировки. В итоге получаю гистограмму представленную выше, по ней можно понять, что на графике присутствуют “выбросы” вначале графика (1 и 2 столбцы), а также в середине (3 и 4 столбец).

Контрольные вопросы.

1. Постановка задачи аппроксимации функций.


2. Чем отличается интерполяция от аппроксимации функций?


3. Что является исходными данными к задаче аппроксимации функций?

4. Постановка задачи аппроксимации функций методом наименьших квадратов.

5. Сущность аппроксимации МНК.


6. Когда применяется метод наименьших квадратов?

7. Определение коэффициента достоверности аппроксимации.


8. Какие действия необходимо выполнить на диаграмме для построения линии аппроксимации?


9. Каким образом задается тип аппроксимации?


10. Что необходимо сделать, чтобы вывести уравнение и величину достоверности аппроксимации?
Ответы на вопросы

1. Основная задача аппроксимации – построение приближенной (аппроксимирующей) функции   наиболее близко проходящей около экспериментально полученных точек 

---

 или заданной непрерывной функции  . В общем смысле термином «аппроксимация» называют замену одних математических объектов другими, например, сложных функций более простой функцией или набором простых функций, в том или ином смысле близкими к исходным.

2. Интерполяция и аппроксимация используются для построения функций по набору данных. Но если в случае аппроксимации кривая должна лишь в некотором смысле приближать данные, интерполяционная функция должна строго совпадать с данными в узлах сетки.

Кроме того, интерполяцию в узком смысле можно понимать как просто поиск промежуточного значения между двумя узлами. А аппроксимацию в более широком смысле можно, например, понимать как замену сложных математических функций более простыми, а также как любые приближения сложных объектов более простыми/удобными/ясными.

3. Исходными данными к задаче аппроксимации функций являются экспериментально полученные точки.

4. Требуется подобрать функцию   соответствующую наилучшему приближению к фактической экспериментальной зависимости  .

5. В этом случае непрерывную функцию   для аппроксимации дискретной зависимости   выбирают из условия наилучшего квадратичного приближения (стандартный метод наименьших квадратов)

. (3.1)

Задачу на поиск минимума   можно свести к задаче поиска корня системы уравнений с неизвестными параметрами , 

---

(3.2)

Подстановка (3.1) в (3.2) приведет к системе   алгебраических уравнений (3.3) относительно неизвестных параметров.

Решая эту систему уравнений, найдем значения параметров   и, следовательно, искомую аппроксимирующую функцию  , удовлетворяющую сформулированным выше требованиям.

6. Этот математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.

7. Коэффициент достоверности аппроксимации - это значение которое характеризует точность аппроксимации, т. е. показывает на сколько точно теоретическое распределение описывает реальное распределение. Находится так: 1 минус сумма отклонения данных точек у от значений аппроксимируемой функции деленная на сумму отклонения данных точек у от среднего значения .

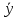8. Создать график, слева записать функцию от переменной, снизу переменную.

9. Находим коэффициент достоверности аппроксимации каждой функции аппроксимации и наиболее подходящим станет та, что по модулю ближе к 1.

10. Чтобы вывести уравнение достоверности аппроксимации необходимо найти уравнение функции аппроксимации f(x), среднее значение точек 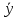, а также сами экспериментальные точки х и у и количество пар n. Чтобы найти величину достоверности аппроксимации надо из 1 вычесть отношение суммы отклонения данных точек у от значений аппроксимируемой функции деленная от суммы отклонения данных точек у от среднего значения

---

Смотрите также файлы

• Глоссарий Термин фразеология.docx

• План проведения практического занятия с дежурным караулом.doc

• Основы теории конфликтного поведения Признак для анализа.docx

• Упразднение традиционной российской адвокатуры Декретом о суде 1 от 22 ноября 1917 г. Создание советской адвокатуры.docx

• Схема лексического анализа слова.doc