Файл: БДР ПЗ 5-06.docx

Цікаво відзначити, що поліпшення чутливості камери на порядок ( до 0,05 лк) збільшує час працездатності системи на 16 хвилин, по 8 хвилин на сході і заході сонця. Звідси випливає, що варіації із чутливістю в діапазоні змін природніх освітленостей (0,01...1,0) лк малоефективні.

Двухмодові гістограми розподілу рівнів природніх освітленостей для липня і грудня місяців (рис. 1.4), свідчать про те, що найбільш ймовірні значення освітленостей у денний час лк, у ночі лк. Крайні ж значення освітленостей ( і ) лк малоймовірні навіть у ці місяці.

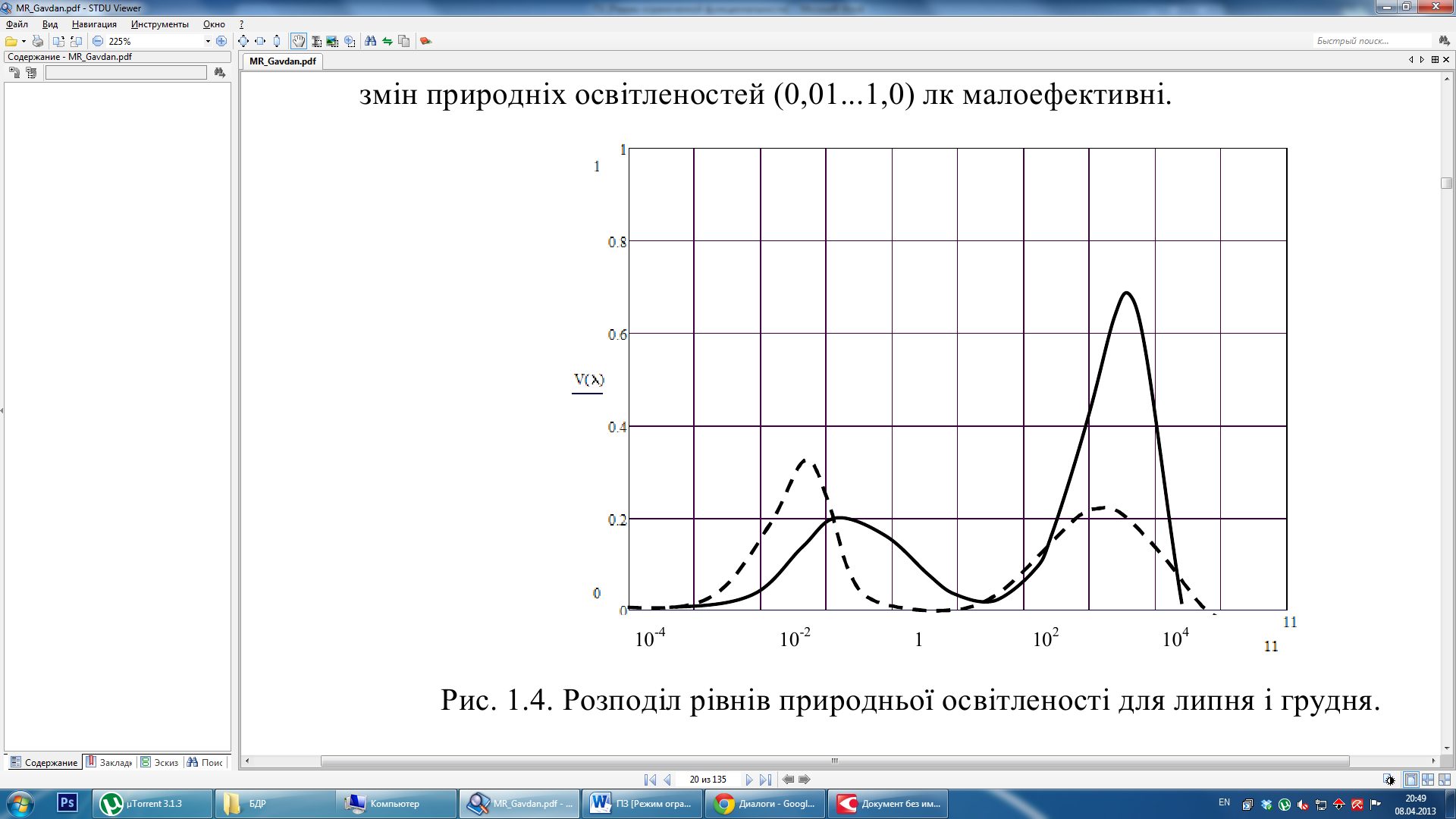
Рисунок 1.4 - Розподіл рівнів природньої освітленості для липня і грудня

Таким чином, питання забезпечення працездатності відеоосистем при освітленості 10⁵ лк хоча й складне завдання але таке, що може бути вирішеним наявними технічними засобами, при цьому менш вартісними ніж при лк. В особливо відповідальних випадках необхідне штучне підсвічування, витрати на енергетику якої залежать від чутливості телевізійних камер. При цьому, виникає питання, що більше прийнятне: груба по чутливості відеокамера у сукупності з потужною підсвіткою, або ж відеокамера високої чутливості з мінімальними енергетичними витратами на подсвітку. У кожному із цих варіантів виникає необхідність визначити границю за рівнем освітленості, коли подсвітка повина бути обов'язково включена і які вимоги до її енергетичних, а також спектральних характеристик повинні бути висунуті.

Як показав аналіз принципу роботи цих засобів, оцінюючи їх ефективність при використанні в охороні кордону на відкритих ділянках в умовах природньої освітленості, необхідно співставляти розподіл освітленості і відносні спектральні характеристики відеосистем конкретної конструкції та принципу роботи. При цьому слід пам'ятати, що за певних екстремальних умов, які притаманні конкретним ділянкам місцевості, вразливість системи спостереження може бути настільки велика, що ефективність її застосування буде зводитись до нуля.

Висновок:

Проведений аналіз стану питання застосування оптико-електронних засобів спостереження в системі інженерно-технічного контролю показав, що ефективність різних засобів спостереження в значній мірі залежить від умов їх застосування, при чому є умови в яких ця ефективність сягає критичних значень.

2 АНАЛІЗ ПОБУДОВИ ОПТИКО-ЕЛЕКТРОННИХ СИСТЕМ СПОСТЕРЕЖЕННЯ

2.1 Математичні моделі сигналів

Одним із основних підходів при синтезі різного роду систем спостереження, є статистичний підхід, оскільки саме при його застосуванні, можливо досягти оптимальних результатів виявлення та розрізнення в умовах дуже складної завадової обстановки. При цьому, сама постановка завдання виявлення та розрізнення базується на припущеннях про види закону розподілу параметрів сигналів та завад, що реєструються. На виході перетворювача системи виявлення, закони розподілу різних параметрів не можуть бути однаковими, це визначається фізичним принципом функціонування. В більшості випадків їх закони розподілу - нормальні, або приводяться до нормальних після перетворень. Вихідні величини, що знімаються з перетворювача, можуть розподілятися по нормальному закону або закону Райса[2,3].

В сучасних методах, процес виявлення зводиться до ухвалення рішення про наявність або відсутність корисного сигналу S(t) шляхом прийому і обробки адитивної суміші його з шумом у(t)= S(t)+ п(t), з подальшим його порівнянням прийнятого коливання з пороговою напругою и_пор (рис. 2.1). Для спрощення математичного аналізу можна вважати, що діє білий нормальний шум[4]. Якщо вирішується задача розрізнення, необхідно виявити дію одного з декількох S1, S2, S3 можливих сигналів. Наприклад, сигнали від техніки (гусеничної, колісної), від людини (одиночної або групи), від крупних тварин (рис. 2.2).

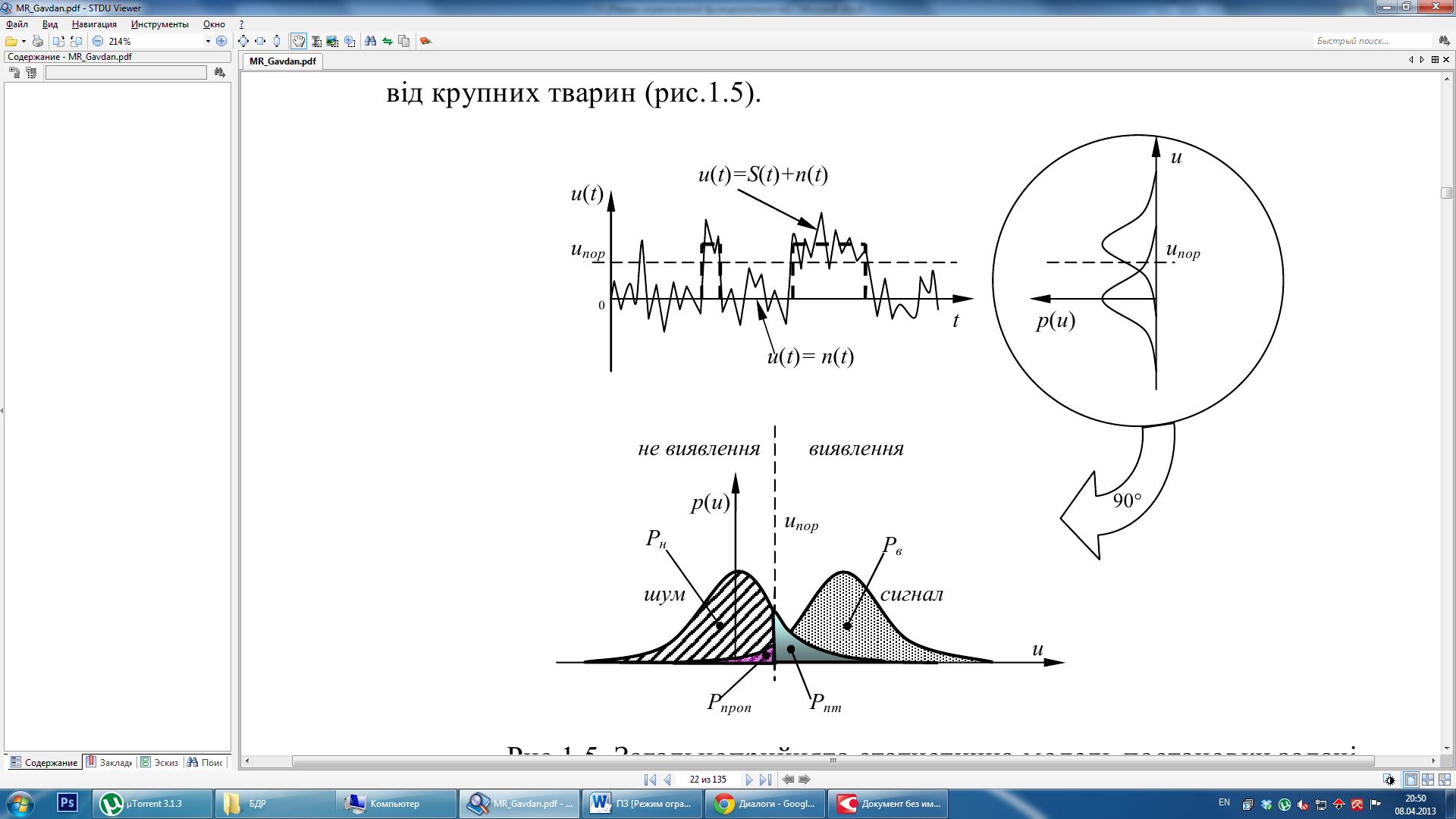
Рисунок 2.1 – Загальноприйнята статистична модель постановки задачі виявлення сигналу на фоні завад

В загальному випадку, процес виявлення вважається окремим випадком розпізнавання, при цьому відбувається розрізнення тільки одного сигналу на фоні перешкод.

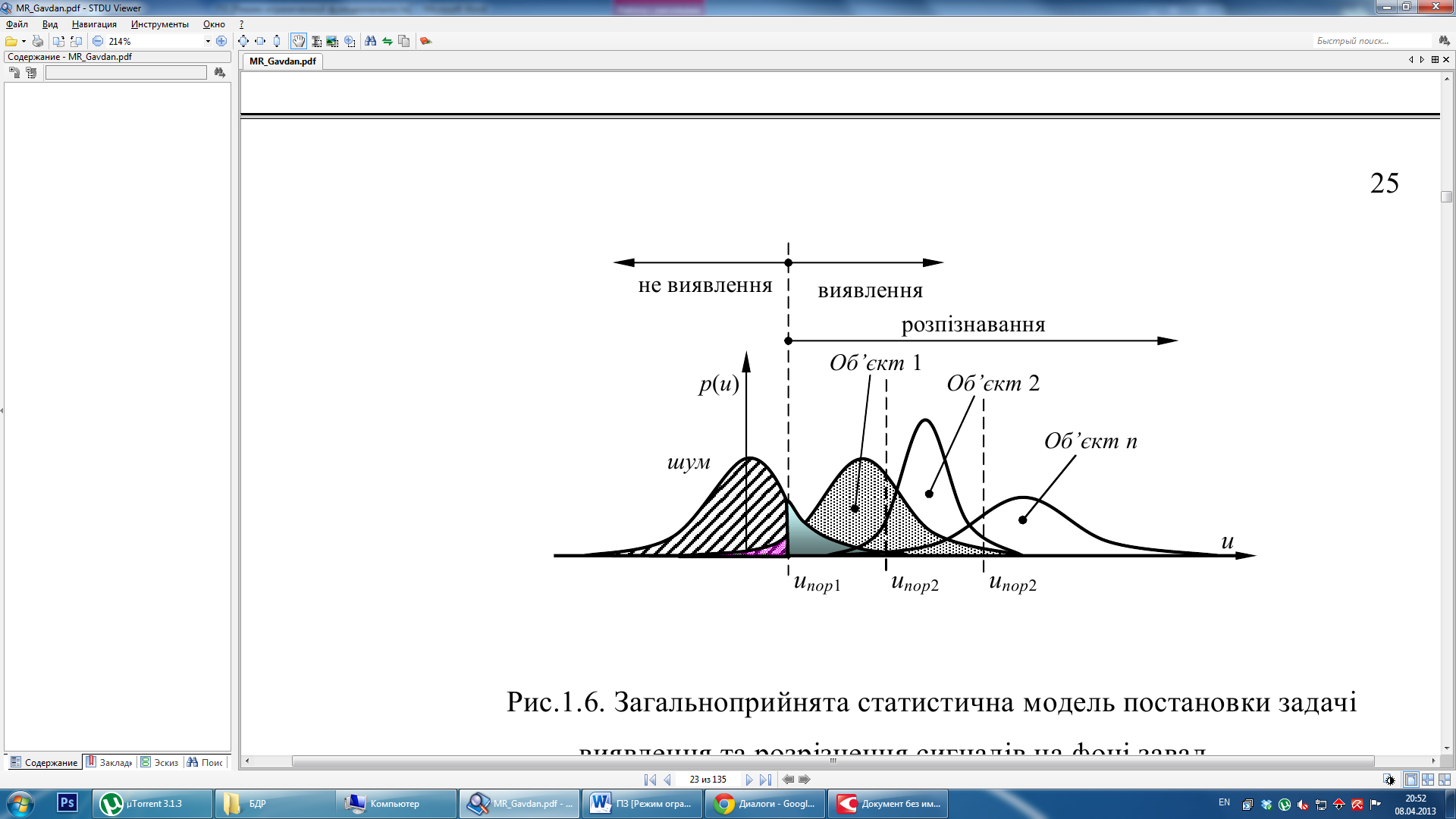
Рисунок 2.2 - Виявлення та розрізнення сигналів на фоні завад

В радіолокації, при вирішенні задачі виявлення, можливе застосування простих гіпотез, а у разі розпізнавання - тільки складних. Як правило приймаються наступні гіпотези: Н₀ - сигналу немає, Н₁ - сигнал є, причому: Р(Н₁)+ Р(Н₀)= 1. При цьому можливі 4 випадки (рис. 2.3).

Рисунок 2.3 - Перевірка гіпотез про наявність сигналу в вхідній суміші

Р(А₁/ Н₁) - умовна ймовірність правильного виявлення Р_пв;

Р(А₀/Н_о) - умовна ймовірність правильного не виявлення Р_нп;

Р(А_о/ Н_і) - умовна ймовірність пропуску сигналу Р_проп^;

Р(А_і/ Н_о) - умовна ймовірність помилкової тривоги Р_пт.

Очевидно, що ймовірнісні характеристики знаходяться у наступному взаємозв'язку

(2.1)

Найважливішими показниками якості системи виявлення є ймовірність виявлення Р_в і ймовірність помилкової тривоги Р_пт. Ймовірність помилкової тривоги визначає напрацювання на помилкове спрацьовування (тривогу). Засіб допускає помилки, коли пропускає сигнал або формує сигнал тривоги за відсутності дії. Сумарна помилка функціонування системи виявлення виражається наступним чином

(2.2)

Ймовірність помилки залежить як від апріорної ймовірності наявності (відсутності) сигналу Р(Н₁ ), Р(Н₀), так і від умовної ймовірності Р_пт і Р_в.

Вираз (2.2) характеризує сумарну помилку ухвалення рішення РТЗ, але не враховує можливий збиток від реалізації цих помилок. Отже, необхідно ввести вагові коефіцієнти помилок, що виникають при помилкових тривогах і пропусках сигналів P_пт ,P_проп, що реалізовано у вигляді наступного виразу:

, (2.3)

де с - середній ризик ухвалення рішення засобом виявлення.

Р_пт і Р_проп можуть виражатися як безпосередньо в значеннях так і у відносних нормованих одиницях.

Відповідно одним з шляхів мінімізації с є максимізація наступної різниці

. (2.4)

Це узагальнений критерій Байєса, інакше - критерій мінімуму середньої

ризику, який записується у вигляді

. (2.5)

Не завжди існує можливість точного визначення втрат від помилок . У такому разі вартості помилок можуть прийматися рівними Р_пт=Р_проп=1 (критерій ідеального спостерігача). При цьому вираз для запишеться у вигляді

. (2.6)

Вираз (2.6) спрощується, коли невідома апріорна ймовірність появи Якщо значення відношення правдоподібності виявляється між порогами (у зоні невизначеності), то випробування (спостереження за сигналом) продовжується. Така процедура в більшості випадків дозволяє скоротити час ухвалення рішення при фіксованих Р_пт і Р_в.

Ймовірність виявлення і помилкової тривоги знаходиться як інтеграл по відповідній щільності розподілу амплітудних значень сигналу з шумом (2.7) і шуму (2.8), по змінним и, що змінюються від порогу U_пор до ∞. Ці вирази записані в припущенні, що параметр, по якому ведеться виявлення, має нормальний розподіл

, (2.7)

. (2.8)

Відповідно до (2.7) і (2.8) максимізується різниця (1.4), при цьому

.(2.9)

З виразу (2.9) видно, що завдання виявлення зводиться до знаходження

відношення правдоподібності при заданому пороговому значенні.

Для одержання максимуму необхідно, щоб .

У разі, коли завада - білий нормальний шум, відношення правдоподібності представляється експонентою (монотонною функцією), отже з нею можна зпівставити поріг виявлення (рисунок 2.4). При цьому, пристрій обробки формує відношення , а пороговий пристрій порівнює з .

Вище розглянутий варіант роботи, коли виявлення ведеться по амплітуді напруги сигналу, виявлення може вестися і по інших параметрах, наприклад, частоті, фазі і так далі. У літературі параметри, по яких ведеться виявлення, класифікуються на енергетичних і неенергетичних[5]. Контрольований параметр може бути розподілений згідно із законом, відмінному від нормального, при цьому загальний сенс вирішення залишається незмінним.

Рисунок 2.4 - Узагальнена структура системи виявлення

Для визначення структури пристрою обробки конкретизують щільність розподілу ймовірності, що входить у відношення правдоподібності. Зазвичай передбачається, що всі параметри сигналу відомі, невідомий тільки факт його наявності. Для спрощення можна вважати, що виявляється дискретний сигнал, оцифрований відповідно до теореми Котельнікова. Елементи вибірки білого шуму Гауса незалежні, щільність Р_ш(и) представляє собою N – мірну щільність ймовірності, яка визначається добутком одновимірних щільностей

. (2.10)

У виразі (2.10) враховане нульове середнє значення шуму. Сигнал и(t) може зміщувати розподіл шуму від нульового математичного очікування або змінювати середнє квадратичне відхилення сигналу (рис. 2.5).

Якщо розглянути випадок, коли дія сигналу призводить до зсуву математичного очікування розподілу (рис. 2.5а), щільність розподілу суміші визначається як

, (2.11)

де т_сk - математичне очікування сигналу в суміші з шумом.

. (2.12)

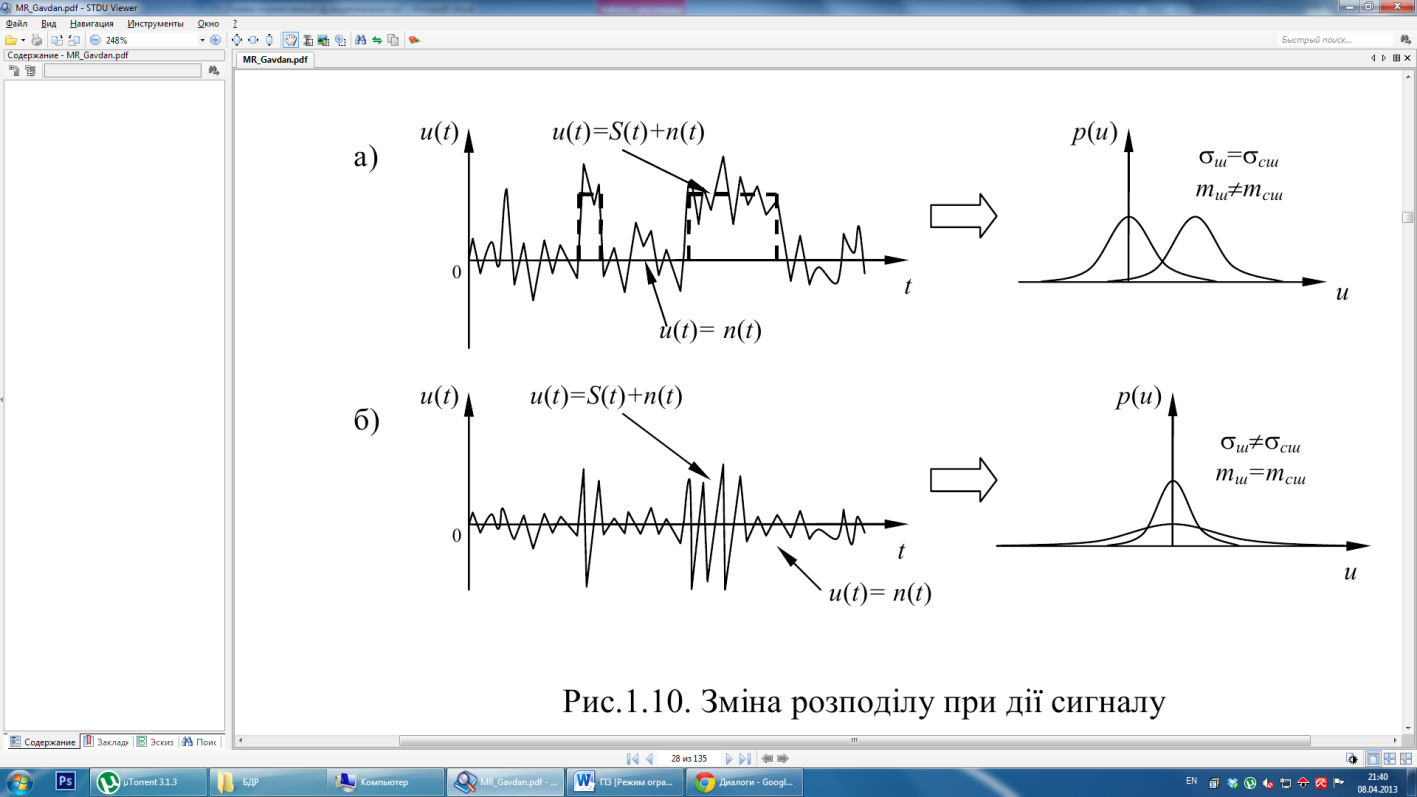
Рисунок 2.5 - Зсув щільності розподілу при дії сигналу

Перший інтеграл в виразі (2.12) - це кореляційний інтеграл між вхідним коливанням і очікуваним сигналом, другий - енергія сигналу (на одиничному опорі). Якщо система виявлення будується за критерієм ідеального спостерігача, то порогова напруга визначається (при однаковій апріорній ймовірності появи сигналу і його відсутності, рівних 0,5, як

. (2.13)

Тоді вирішальне правило приймає вигляд

. (2.14)

Для критерію Неймана-Пірсона поріг виявлення запишеться

. (2.15)

Якщо використовується критерій послідовного спостерігача, то необхідно мати два пороги, нижній і верхній (2.16), (2.17)

(2.16)

(2.17)

Структура кореляційного пристрою виявлення (рис. 2.6) будується на основі кореляційного інтеграла, максимальне значення якого рівне .

. (2.18)

На перемножувач поступає сигнал и(t), який є сумішшю корисного сигналу і шуму. Одночасно на другий вхід перемножувача поступає опорний сигнал S(t), який є точною копією очікуваного (що виявляється) сигналу з точністю до фази. Протягом часу ведеться інтегрування.

Рисунок 2.6 - Кореляційний пристрій виявлення

Після закінчення часу інтегрування результат накопичення комутується до входу ПП, проводиться порівняння з опорним сигналом. Пристрій синхронізації забезпечує послідовність функціонування всіх пристроїв з точністю до фази.

Якщо S(t) виразити через імпульсну характеристику h(Т-t), то кореляційний інтеграл запишеться у вигляді інтеграла згортки

. (2.19)