ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.12.2021
Просмотров: 1083
Скачиваний: 3
СОДЕРЖАНИЕ
3.6. Побудова дискретної математичної моделі електронного зображення ……
Рисунок 3.4 – Структурна схема системи відеоспостереження
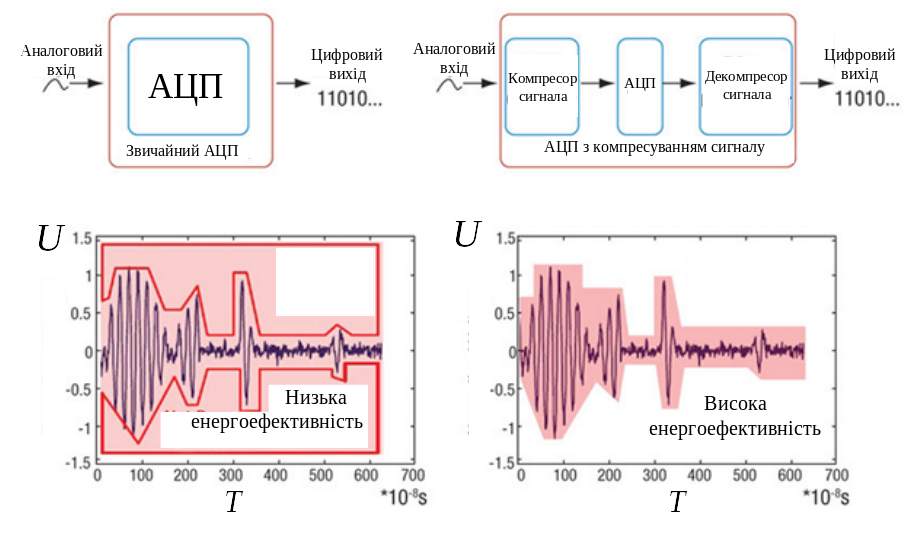
3.5 Аналогово-цифрове перетворення в оптико-електронних системах спостереження
а) звичайне квантування по амплітуді б) квантування по амплітуді з стисненням
Рисунок 3.5 – Квантування сигналу по амплітуді
Рисунок 3.6 – Інтегральна функція розподілу сигналу
3.6. Побудова дискретної математичної моделі електронного зображення
Нехай {Zn} - множина «сигнальних» послідовностей Zn довжиною п, з появою кожної з яких на вході виявляча ухвалюється рішення про присутність об'єкту. Якщо «сигнальні» послідовності визначені для всіх п, то цим самим визначене деяке вирішальне правило R(Zп). Таким чином, для оптимізації процесу виявлення об'єкту необхідно для всіх значень п знайти такі «сигнальні» множини, при яких виконуються умови оптимальності.
Розглянемо
наступну подію: об'єкт з'являється в
зоні спостереження між
(k
— 1)-м
і
k-м
оглядами (кадрами) і виявляється в
результаті надходження на вхід виявляча
деякої послідовності
,
що
входить в
«сигнальну» множину
{Zn}.
Ймовірність даної події при прийнятих
припущеннях визначається за формулою[8]
(3.10)
де n0 – середня кількість оглядів (кадрів) між суміжними неправильними виявленнями об'єкту. Якщо прийняти величину інтервалу між суміжними кадрами за одиницю часу, то n0=t0.
Час існування об'єкту до виявлення за умови реалізації розглянутої події дорівнює п-k+0.5, де інтервал 0,5 є середнім часом перебування об'єкту в зоні спостереження до моменту першого огляду. Середній час існування об'єкту до виявлення визначається виразом
(3.11)
де Мп - кількість різних «сигнальних» послідовностей, що входять у множину {Zn}.
Нехай Zn1=(Z11,Z21,…,Zn1) і Zn2=(Z12,Z22,…,Zn2) - дві можливі послідовності довжиною п такі, що
(3.12)
Розглянемо два варіанти формування «сигнальних» множин {Zn}, кожному з яких відповідає певний спосіб виявлення об'єкту. При першому способі послідовність Zп1 входить в «сигнальну» множину {Zn}, а послідовність Zп2 є складовою частиною (початком) деякої сукупності Q «сигнальних» послідовностей більшої довжини. Другий спосіб відрізняється від першого тим, що зазначені послідовності міняються місцями, тобто Zп2 входить в «сигнальну» множину {Zn}, а послідовність Zп1 є складовою частиною (початком) зазначеної вище сукупності Q «сигнальних» послідовностей більшої довжини, замінивши в них послідовність Zn2.
Внаслідок останньої рівності (3.12) послідовності Zп1 і Zп2 при відсутності об'єкту рівноймовірні. Тому при розглянутих способах виявлення, закони розподілу ймовірностей інтервалу t0 однакові.
Використовуючи
формулу (3.11)
визначається різниця
,
між значеннями часу існування об'єкту
до виявлення
при першому і другому способах виявлення.
При оцінці різниці
слід врахувати, що складові правої
частини виразу (3.11)
які не містять послідовностей
Zп1
і
Zп2
мають однакові значення при обох способах
виявлення. Крім того, однакові значення
мають і доданки, які містять послідовності
Zп1
і
Zп2,
якщо ці доданки відповідають індексу
k
>
п.
Відповідно до
останніх зауважень, різниця
,
визначається з виразу
,
(3.13)
де
- одна з послідовностей, що доповнюють
послідовність Zп2,
при першому і послідовність
Zп1
при другому способах виявлення, до
однієї з «сигнальних» послідовностей
множини {Zn};
М* - кількість послідовностей Z* при заданому значенні п. У перших фігурних дужках останнього виразу приведено складові величини t1, при першому способі виявлення, у других - при другому.
Аналізуючи отриманий
вираз, легко можна виявити, що
<
0 тільки тоді, коли послідовності
Zп1
і
Zп2
задовольняють
умові
(3.14)
А отже, використовуючи
отриманий вираз, можна сформулювати
правило формування «сигнальних» множин
{Zn},
п=1,2,...
при яких забезпечується мінімум
,
при заданому розподілі ймовірностей
Р(t0)
інтервалу
t0
між неправильними виявленнями об'єкту.
При чому, це правило буде полягати в
наступному: «сигнальна» множина {Zn}
містить всі послідовності
Zп„
що задовольняють умові:
(3.15)
де константа Сп вибирається таким чином, щоб ймовірність виконання умови (3.15) при відсутності об'єкту, дорівнювала заданому значенню ймовірності Р(t0=п).
При фіксованому значенні ймовірності Р(t0=п) будь-яка сигнальна множина, що не співпадає повністю із визначеною нерівністю (3.15) буде містити послідовності Zп„ при яких
(3.16)
а це відповідно
(3.14)
призведе лише до збільшення
.
Таким чином, при
розв'язанні задачі виявлення сторонніх
об'єктів в системах відеоспостереження,
вага ймовірності пропуску сигналу в
загальній ефективності алгоритму
обробки сигналів значно вище ніж при
вирішенні задач радіолокації чи в
асинхронних системах передачі даних,
оскільки період огляду в таких системах
є не одновимірним. В результаті, при
незначному коливанні значень середнього
часу не виявлення
,
границя між умовами (3.15)
та (3.16)
стає нечіткою і постає гостра необхідність
зниження значення
Сп,
що в даних умовах є небажаним.
3.3 Удосконалення алгоритмів виявлення в оптико-електронних системах спостереження
Як стало
видно із останніх виразів, в системах
відеоспостереження застосовувати
класичні методи побудови оптимальних
виявлячів недоцільно, в першу чергу
через те, що при обробці сигналів з
виходу відеореєстратора є певні
особливості в співвідношенні часових
інтервалів огляду і наявності об'єктів.
Основним
індикатором цих особливостей, є висока
залежність ймовірності виявлення
об'єкту від середнього часу не виявлення,
при знаходженні його в зоні спостереження.
А отже, за таких умов, метод виявлення
об'єкту, що з'являється в невизначений
момент часу
і при якому, для заданого розподілу
ймовірностей
Р(t0),
середній час існування об'єкту до
виявлення найменший,
полягає в наступному: при кожному
значенні n=1,2,3,
обчислюється величина відношення
правдоподібності
,
що визначається з виразу
(3.17)
де
-
відношення правдоподібності для множини
відліків
сигналу при наявності об'єкту в зоні
спостереження, рішення про появу об'єкту
приймається, якщо при деякому
п
ця величина перевищує поріг
Сп.
Величину
в
даному випадку, можна записати в
наступному вигляді
(3.18)
де
(3.19)
(3.20)
Оскільки
(3.21)
то з формули (3.18) отримуємо
(3.22)
Рисунок 3.1 - Структурна схема пристрою виявлення сторонніх об'єктів на
відеозображенні
Відповідно цього співвідношення, оптимальний пристрій виявлення об'єкту при реалізації системи відеоспостереження, містить перемножувач, суматор, пристрій пам'яті, і попроговий пристрій (рисунок 3.1).
В
даній структурі, запам'ятовуючий пристрій
зберігає вихідну величину перемножувача
протягом періоду проходження відліків
послідовності Zn,
реалізуючи рекурентність обробки, а
пороговий пристрій виробляє сигнал
наявності цілі, якщо вихідна величина
перевищує
поріг
Сп.
Описаний метод виявлення відповідає таким умовам, при яких об'єкт, з'явившись у зоні спостереження, залишається в ній до виявлення. Якщо час перебування об'єкту обмежений і дорівнює r періодам огляду (кадрам), то нижню межу суми по k слід прийняти рівною n — r + 1. При цьому в виявлячі при кожному значенні п обчислюється і порівнюється з порогом Сп величина
(3.23)
Останній вираз можна записати у вигляді
(3.24)
де
(3.25)
Пристрій виявлення об'єктів для розглянутих умов відрізняється від попереднього додатковим блоком пам'яті і схеми віднімання (рис. 3.2).
Рисунок 3.2 – Структурна схема пристрою виявлення при обмеженому часі перебування об'єкту в зоні спостереження
Запам'ятовуючий
пристрій призначений для зберігання
величини
протягом
r
періодів огляду. Цей блок повинен мати
r-1
комірок пам'яті для зберігання наступних
величин:
,
,..,
.
Схема віднімання формує різницю
величин
і
,
перша з яких надходить із виходу
перемножувача а друга з блоку пам'яті.
Запропонований
метод виявлення об'єктів передбачає
необхідність включення в обчислення
при кожному значенні n,
величину
усіх
відліків спостережуваної послідовності
Zn,
починаючи з n=1.
Якщо об'єкт з моменту появи і до виявлення
може перебувати в різних елементах
розрізнення контрольованої зони, то
кількість можливих траєкторій об'єкту,
для кожної з яких у пристрої виявлення
повинна обчислюватися величина відношення
правдоподібності, може бути дуже великою,
а пристрій виявлення занадто складним.
У зв'язку з цим, замість рекурентного співвідношення (3.22) можна використати спрощений варіант
(3.26)
При цьому, рішення
про появу об'єкта видається в тому
випадку, коли
,
де поріг
С
не залежить від
n
і вибирається виходячи з необхідності
забезпечення заданого значення
.
Перехід до даного
співвідношення заснований на використанні
правила «відбору більшого значення».
Дане правило полягає в тому, що
приймається
найбільшим із двох:
або
.
Перша із цих величин представляє собою
коефіцієнт правдоподібності, що
відповідає гіпотезі «об'єкт з'явився
між
(п-1)-м
і n-м
періодами огляду». Друга дорівнює
найбільшому з
п-1
коефіцієнтів правдоподібності, кожний
з яких відповідає одній з наступних
гіпотез: «об'єкт з'явився перед першим
оглядом», «об'єкт з'явився перед другим
оглядом», ... «об'єкт з'явився перед
(п-1)-м
оглядом». Таким чином, вираз (3.26)
визначає найбільший з
п коефіцієнтів
правдоподібності, кожний з яких відповідає
або одній з перерахованих гіпотез, або
гіпотезі «об'єкт з'явився перед
п-м
оглядом».
Характер зміни
величини
в області її значень менших одиниці,
можна не фіксувати в процесі обробки,
тобто при
вважається
.
Таким чином, «сигнальна» множина буде містити у собі всі послідовності Zn , що задовольняють умові
,
(3.27)
де
.
(3.28)
Особливість
розглянутого методу виявлення об'єкту
полягає в тому, що величина
ухвалює значення, що дорівнює одиниці,
якщо при деякому
п
виконується умова
.
При цьому послідовність
Zn
виключається
з обробки. Зазначена
особливість призводить до істотного
спрощення пристрою обробки при виявленні
рухомих об'єктів.
Замість величини
у
пристрої простіше обчислювати її
логарифм
і
порівнювати його з порогом
lgС.
Логарифмуючи обидві частини виразу,
одержуємо:
(3.29)
де
(3.30)
Описаний метод
виявлення тотожний з методом послідовного
спостерігача у випадку, коли нижній
поріг дорівнює одиниці. Пристрій
виявлення об'єкту при використанні
даного методу містить блок формування
величини
,
суматор, блок пам'яті і пороговий пристрій
(рисунок
3.3).
Рисунок
3.3 –
Структурна
схема пристрою
виявлення об'єкту методом послідовного
аналізу
Відповідно данної
схеми, в суматорі проводиться додавання
величин
і
.
Якщо сума цих величин
від'ємна,
то її значення приймається нульовим.
Пороговий пристрій видає сигнал про
наявність об'єкту, якщо
.
Підсумовуючи викладене, слід зазначити, що при виявленні стороннього об'єкту на електронному зображенні, поряд з розглянутими методами можуть використовуватися так звані серійні критерії виявлення. В останньому випадку рішення про появу об'єкту, що видається після надходження у виявляч відліку Zп,визначається к відліками послідовності Zn =zп-k+1, zп-k+2, , де k - задане число. Порівняння запропонованого методу послідовного аналізу і серійних критеріїв показує, що цей метод забезпечує значно менший час Сn при виявленні слабких сигналів.
3.4 Структура оптико-електронної системи та особливості представлення електронного зображення в дискретній формі
Широке застосування цифрових технологій при реалізації систем відеоспостереження, практично зняло обмеження на їх динамічний діапазон в відношенні освітленості об'єктів спостереження. При цьому, застосування відеокамер з вбудованими модулями аналогово-цифрового перетворення дало змогу значно підвищити завадостійкість каналів передачі відеоінформації на відстань і як наслідок усунути зашумленість зображень, що з'являється при їх передачі. Найчастіше такі камери забезпечуються також вбудованими схемами керування чутливістю, фокусуванням і іншими параметрами, які можуть контролюватися як самим вбудованим модулем, так і ЕОМ. Структурна схема системи відеоспостереження в цьому випадку буде мати вигляд, що показаний на рисунку 3.4.
Рисунок 3.4 – Структурна схема системи відеоспостереження
Для формалізації зображення об'єктів, що перебувають в полі зору відеокамери і формуються на поверхні світлочутливого елементу у вигляді плоского дискретного світлового поля, в довільний момент часу, можна представити в вигляді кінцевого набору величин освітленості елементів ПЗЗ- матриці[3]. У випадку використання монохромних відеокамер зображення представляється у вигляді функції яркісної компоненти
Y Y (x, y). (3.31)
При використанні кольорових відеокамер необхідно характеризувати значення величин трьох основних колірних складових - червоної, зеленої й синьої
R R (x, y), (3.32)
G G (x, y), (3.33)
B B (x, y). (3.34)
У силу того, що вимірювання зазначених величин проводиться за допомогою аналого-цифрового перетворювача, значення функцій , так само як і їхні аргументи будуть дискретними.