ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 73
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В июле 2018 года в Казахстане впервые отметили День домбры. На протяжении веков домбра была тесно связана с историей, культурой и повседневной жизнью казахского народа. Примечательно, что в республике целый день в году решили обозначить днем музыкального инструмента, и этим инструментом стала домбра. Домбра — это символ музыкальной культуры от кочевников древности и до сегодняшнего дняИнструменты, напоминающие домбру, существовали с незапамятных времен. Если верить камням с наскальными изображениями танцующих людей, выставленным в музее народных музыкальных инструментов имени Ыкыласа, наши предки играли на них более 4 тысяч лет назад. Тем не менее, первые достоверные сведения о домбре появляются лишь в XVI–XVII веках. Предком домбры является древнетюркский музыкальный инструмент шертер. По форме он напоминает домбру, но имеет открытый корпус, три струны и короткий гриф без ладов. Шертер изготавливали из цельного куска дерева, а на корпус натягивали кожаную деку. Играли на шертере как щипком или ударом по струнам, так и с помощью смычка. От шертера произошли кобыз и домбра. Традиционно мастера выдалбливали домбру из цельного куска дерева. В качестве материала использовали любые породы деревьев, которые росли в данной местности. Со временем, для улучшения акустических свойств инструмента, изменился метод его изготовления. Домбру начали делать из отдельных склеенных деталей, а в качестве сырья стали выбирать твердые породы древесины — сосну, лиственницу, ель.Одно из главных отличий современной домбры от инструментов, на которых играли Курмангазы и Даулеткерей, — струны. Сейчас их делают из лески, но до начала XX века на домбре использовали жильные струны, изготовленные путем сложного процесса выделки бараньих или козьих кишок.— Леска звучит очень ярко и мощно, но жильные струны дают особый колорит, очень глубокий и мягкий звук. Лады — по-казахски их называют «перне» — тоже делали из жил. Благодаря этому звук традиционной домбры богат на обертоны и призвуки.По мнению музыковеда, феномен домбры заключается в ее глубине и многообразии. Она может звучать, как целый оркестр, передавая широкую палитру звука. Такая музыка находит отклик в душе слушателей и вступает в резонанс с человеческой психикой. Длинный гриф, округлая форма, мягкие материалы и жильные струны — такая простая конструкция создает идеальную акустику. Казахская народная музыка
, которую сочиняли и исполняли на домбре, это сложное, яркое и абстрактное искусство. Поэзия в нем неразрывно связана с музыкой. Произведения известных жырау, салов и акынов через музыку и устное творчество осмысливают вечные философские вопросы. — Творчество кюйши и акынов затрагивает глубокие темы. Его нельзя воспринимать буквально. Если во время звучания кюя кажется, что слышишь топот конских копыт, то нужно понимать, что автор хотел передать не бег лошади, а впечатление от этого бега в своей душе. Казахское искусство очень содержательно и философично, оно носит в себе много смыслов. Домбра играла важную роль в жизни не только профессиональных исполнителей и акынов, но и простых кочевников-скотоводов. Домбра была непременным атрибутом в каждой юрте и висела на почетном месте на кереге. Дети обучались музыке, играя на миниатюрной домбре — шинкилдеке. Взрослые знали мотивы известных песен и кюев и могли наиграть простейшие из них. Нельзя утверждать, что домбра — это уникальное и неповторимое изобретение казахов. У многих народов есть аналоги, но домбру можно назвать одним из потрясающих вариантов музыкального совершенства. Этот простой на первый взгляд инструмент способен выразить самые глубокие переживания человеческой души. В прошлом он был тесно связан с казахским народом, и я надеюсь, что так будет и в будущем.
Связь математики и музыки.
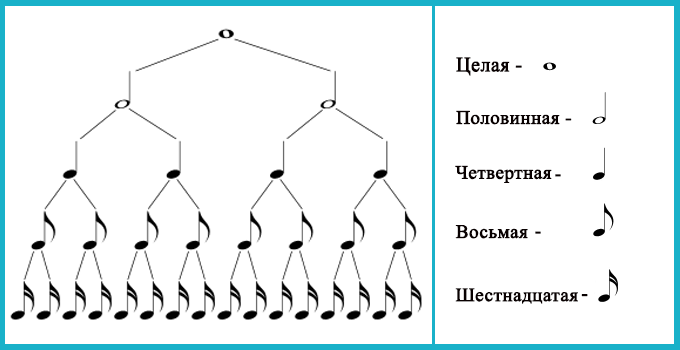
Математика (др.-греч. μᾰθημᾰτικά < др.-греч. μάθημα — изучение, наука) — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов. Математические объекты создаются путём идеализации свойств реальных или других математических объектов и записи этих свойств на формальном языке [4]. Музыка (греч. μουσική, субстантивированное прилагательное от греч. μούσα — муза) — вид искусства. Согласно А.Н.Сохору этот вид «отражает действительность и воздействует на человека посредством осмысленных и особым образом организованных по высоте и во времени звуковых последований, состоящих в основном из тонов». В Большой российской энциклопедии музыка определяется как «искусство звуков, организованных главным образом по высоте и во времени» [4]. Что же общего есть у математики с музыкой? 1. Цифровые обозначения. Как и в математике, в музыке встречаются цифры: звукоряд – 7 нот, нотный стан – 5 линеек. Интервалы: прима – 1, секунда – 2, терция – 3, кварта – 4, квинта – 5, секста – 6, септима – 7, октава – 8. Обозначения аппликатуры и размер произведения записывается тоже при помощи цифр. 2. Наличие в музыке и математике противоположностей. Математика: плюс – минус, больше – меньше, сложение – вычитание, умножение – деление. Музыка: мажор – минор, быстро – медленно, тихо – громко, низко – высоко. 3. Использование дробей. В пятом классе ребята начинают знакомство с дробями на уроках математики. Те, кто посещают музыкальную школу, знакомятся с дробями намного раньше. В целой ноте - две половинных, четыре четвертных, восемь восьмых, 16 шестнадцатых. Таким образом, длительности нот получаются так же, как и дроби: они возникают при делении целой на равные доли. Поэтому длительность можно подсчитывать так же как дробные числа: 1/2, 1/4, 1/8, 1/16. Следовательно, названия длительностей служат одновременно и названиями чисел (Приложение 1). 4. Пропорции. В мензуральной музыке так называются обозначения темпа посредством или, наоборот многих других дробей. Пропорция определяла длительность нот или по отношению к непосредственно предшествовавшим длительностям (так, знак после предшествовавшего Integer valor — требовал втрое большей скорости (3 breves= 1 brevis); знак , напротив, 7 требовал втрое меньшей скорости [1=3]). В математике также есть понятие пропорции, которое широко используется при решении задач. 5. Ритм. Ритм важнейший элемент в музыке. У каждого музыкального произведения свой ритмический рисунок (чередование нот разной длительности). Числа, оказывается, тоже обладают ритмом. Например, числа кратные 3(трём) обладают следующим ритмом: начнем с 0 и, увеличивая каждый раз на 1, будем акцентировать все числа, кратные 3. Получается 0 1 2 3 4 5 6 7 8…. и т.д. Получается красивый, правильный, равномерный ритм, звучащий как музыкальный размер 3/4, который соответствует вальсу. Если посчитать числа, кратные двум 0 1 2 3 4 5 6 7 8 9 и т.д. то увидим, что мы пришли к ритму, звучащему, как музыкальный размер 2/4. Таким образом, числа обладают ритмом. 6. Параллельность и параллели. Музыка записывается с помощью нот на нотном стане, который представляет собой, пять параллельных прямых. Параллельно может звучать голос исполнителя и инструмент аккомпаниатора со сдвигом на октаву. Либо параллельно могут звучать голоса в хоре при исполнении многоголосия. Понятие параллельности существует и в математике. 7. Симметрия. Некоторые музыкальные формы строятся симметрично. Например, рондо. В рондо музыкальная тема многократно повторяется, чередуясь эпизодами различного содержания. Главная тема проводится не менее трех раз в основной тональности, а эпизоды – в других тональностях. Это похоже на зеркальную симметрию, где главная тема – плоскость зеркала от которой отражаются эпизоды. 8. Прогрессия. Геометрическая прогрессия – числовая последовательность, первый член которой отличен от нуля, а каждый последующий равен предыдущему, умноженному на одно и то же число. Именно принципу геометрической прогрессии соответствует принцип построения длительностей. Запишем длительности, начиная с единицы в порядке убывания: 1, 1 2 , 1 4 , 1 8 , 1 16 , 1 32 … Получим убывающую геометрическую прогрессию со знаменателем 1 2 . 9. Вариации. В музыке это форма произведения, состоящего из нескольких частей звучащих с изменениями. Композитор берет главную тему и может изменять её ритм и гармонию, мелодический рисунок, то есть созвучия. Число тоже можно записать или определить разными способами. Например, завись числа с помощью цифр или словесная запись (100 или сто).
Любое музыкальное произведение можно представить, как некую математическую модель, которая будет иметь числовую закономерность.
Метод проблемно-поисковой ситуации
История исследования связи музыки с математикой
Математика – царица наук, тесным образом перекликается с музыкой.
Музыка и ее первый звук родились одновременно с творением мира, как утверждали древние мудрецы.
В своих трудах ученые неоднократно делали попытки представить музыку как некую математическую модель. Приведем, к примеру, одну из цитат из работы Леонарда Эйлера “Диссертация о звуке”, написанная в 1727 году: “Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке из правильных оснований все, что может сделать приятным объединение и смешивание звуков”.
Рассматривать музыку, как один из объектов математики, пытались многие величайшие математики. Исследованию музыки посвятил свой первый труд Рене Декарт («Трактат о музыке»), Готфрид Лейбниц, Христиан Гольдбах, Жан Д’Аламбер, Даниил Бернулли и другие. В своих трудах они хотели представить музыку как некую математическую модель. Леонард Эйлер («Диссертация о звуке», 1727 г.) пишет: «Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке из правильных оснований всё, что может сделать приятным объединение и смешивание звуков». Об отношении к математике и музыке ученые высказывались в своих личных переписках. Лейбниц в письме Гольдбаху пишет: "Музыка есть скрытое арифметическое упражнение души, не умеющей считать". На что Гольдбах ему отвечает: "Музыка - это проявление скрытой математики".
Слова мелодия, ритм родились в Элладе, название слова «гамма» происходит от греческой буквы (гамма). После создания точной математической теории струны, поняв, что любой музыкальный инструмент – всего-навсего «физико-акустический прибор», музыку уже не отделить от математики. Математическому анализу подлежат и звук, и тембр, и лад, и гармония. Пифагор создал математическую теорию музыки, слушая, как звучат медные чаши. Каждое настоящее искусство имеет свою теорию, которую можно выразить в терминах математики. Математики, начиная с Пифагора, постоянно проявляли интерес к музыке.
Именно Пифагор был первым, кто попытался выразить красоту музыки с помощью чисел. Он создал свою школу мудрости, положив в ее основу два предмета – музыку и математику. Музыка, как одно из видов искусств, воспринималась наряду с арифметикой, геометрией и астрономией как научная дисциплина, а не как практическое занятие искусством.
Пифагор считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Он был не только философом, но и математиком, и теоретиком музыки. Пифагор основал науку о гармонии сфер, утвердив ее, как точную науку. Известно, что пифагорейцы пользовались специальными мелодиями против ярости и гнева.
, которую сочиняли и исполняли на домбре, это сложное, яркое и абстрактное искусство. Поэзия в нем неразрывно связана с музыкой. Произведения известных жырау, салов и акынов через музыку и устное творчество осмысливают вечные философские вопросы. — Творчество кюйши и акынов затрагивает глубокие темы. Его нельзя воспринимать буквально. Если во время звучания кюя кажется, что слышишь топот конских копыт, то нужно понимать, что автор хотел передать не бег лошади, а впечатление от этого бега в своей душе. Казахское искусство очень содержательно и философично, оно носит в себе много смыслов. Домбра играла важную роль в жизни не только профессиональных исполнителей и акынов, но и простых кочевников-скотоводов. Домбра была непременным атрибутом в каждой юрте и висела на почетном месте на кереге. Дети обучались музыке, играя на миниатюрной домбре — шинкилдеке. Взрослые знали мотивы известных песен и кюев и могли наиграть простейшие из них. Нельзя утверждать, что домбра — это уникальное и неповторимое изобретение казахов. У многих народов есть аналоги, но домбру можно назвать одним из потрясающих вариантов музыкального совершенства. Этот простой на первый взгляд инструмент способен выразить самые глубокие переживания человеческой души. В прошлом он был тесно связан с казахским народом, и я надеюсь, что так будет и в будущем.
Связь математики и музыки.
Математика (др.-греч. μᾰθημᾰτικά < др.-греч. μάθημα — изучение, наука) — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов. Математические объекты создаются путём идеализации свойств реальных или других математических объектов и записи этих свойств на формальном языке [4]. Музыка (греч. μουσική, субстантивированное прилагательное от греч. μούσα — муза) — вид искусства. Согласно А.Н.Сохору этот вид «отражает действительность и воздействует на человека посредством осмысленных и особым образом организованных по высоте и во времени звуковых последований, состоящих в основном из тонов». В Большой российской энциклопедии музыка определяется как «искусство звуков, организованных главным образом по высоте и во времени» [4]. Что же общего есть у математики с музыкой? 1. Цифровые обозначения. Как и в математике, в музыке встречаются цифры: звукоряд – 7 нот, нотный стан – 5 линеек. Интервалы: прима – 1, секунда – 2, терция – 3, кварта – 4, квинта – 5, секста – 6, септима – 7, октава – 8. Обозначения аппликатуры и размер произведения записывается тоже при помощи цифр. 2. Наличие в музыке и математике противоположностей. Математика: плюс – минус, больше – меньше, сложение – вычитание, умножение – деление. Музыка: мажор – минор, быстро – медленно, тихо – громко, низко – высоко. 3. Использование дробей. В пятом классе ребята начинают знакомство с дробями на уроках математики. Те, кто посещают музыкальную школу, знакомятся с дробями намного раньше. В целой ноте - две половинных, четыре четвертных, восемь восьмых, 16 шестнадцатых. Таким образом, длительности нот получаются так же, как и дроби: они возникают при делении целой на равные доли. Поэтому длительность можно подсчитывать так же как дробные числа: 1/2, 1/4, 1/8, 1/16. Следовательно, названия длительностей служат одновременно и названиями чисел (Приложение 1). 4. Пропорции. В мензуральной музыке так называются обозначения темпа посредством или, наоборот многих других дробей. Пропорция определяла длительность нот или по отношению к непосредственно предшествовавшим длительностям (так, знак после предшествовавшего Integer valor — требовал втрое большей скорости (3 breves= 1 brevis); знак , напротив, 7 требовал втрое меньшей скорости [1=3]). В математике также есть понятие пропорции, которое широко используется при решении задач. 5. Ритм. Ритм важнейший элемент в музыке. У каждого музыкального произведения свой ритмический рисунок (чередование нот разной длительности). Числа, оказывается, тоже обладают ритмом. Например, числа кратные 3(трём) обладают следующим ритмом: начнем с 0 и, увеличивая каждый раз на 1, будем акцентировать все числа, кратные 3. Получается 0 1 2 3 4 5 6 7 8…. и т.д. Получается красивый, правильный, равномерный ритм, звучащий как музыкальный размер 3/4, который соответствует вальсу. Если посчитать числа, кратные двум 0 1 2 3 4 5 6 7 8 9 и т.д. то увидим, что мы пришли к ритму, звучащему, как музыкальный размер 2/4. Таким образом, числа обладают ритмом. 6. Параллельность и параллели. Музыка записывается с помощью нот на нотном стане, который представляет собой, пять параллельных прямых. Параллельно может звучать голос исполнителя и инструмент аккомпаниатора со сдвигом на октаву. Либо параллельно могут звучать голоса в хоре при исполнении многоголосия. Понятие параллельности существует и в математике. 7. Симметрия. Некоторые музыкальные формы строятся симметрично. Например, рондо. В рондо музыкальная тема многократно повторяется, чередуясь эпизодами различного содержания. Главная тема проводится не менее трех раз в основной тональности, а эпизоды – в других тональностях. Это похоже на зеркальную симметрию, где главная тема – плоскость зеркала от которой отражаются эпизоды. 8. Прогрессия. Геометрическая прогрессия – числовая последовательность, первый член которой отличен от нуля, а каждый последующий равен предыдущему, умноженному на одно и то же число. Именно принципу геометрической прогрессии соответствует принцип построения длительностей. Запишем длительности, начиная с единицы в порядке убывания: 1, 1 2 , 1 4 , 1 8 , 1 16 , 1 32 … Получим убывающую геометрическую прогрессию со знаменателем 1 2 . 9. Вариации. В музыке это форма произведения, состоящего из нескольких частей звучащих с изменениями. Композитор берет главную тему и может изменять её ритм и гармонию, мелодический рисунок, то есть созвучия. Число тоже можно записать или определить разными способами. Например, завись числа с помощью цифр или словесная запись (100 или сто).
Любое музыкальное произведение можно представить, как некую математическую модель, которая будет иметь числовую закономерность.
-
Изучение, обработка и анализ документов и интернет - источников. -
Исследование музыкального произведения .
Метод проблемно-поисковой ситуации
История исследования связи музыки с математикой
Математика – царица наук, тесным образом перекликается с музыкой.
Музыка и ее первый звук родились одновременно с творением мира, как утверждали древние мудрецы.
В своих трудах ученые неоднократно делали попытки представить музыку как некую математическую модель. Приведем, к примеру, одну из цитат из работы Леонарда Эйлера “Диссертация о звуке”, написанная в 1727 году: “Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке из правильных оснований все, что может сделать приятным объединение и смешивание звуков”.
Рассматривать музыку, как один из объектов математики, пытались многие величайшие математики. Исследованию музыки посвятил свой первый труд Рене Декарт («Трактат о музыке»), Готфрид Лейбниц, Христиан Гольдбах, Жан Д’Аламбер, Даниил Бернулли и другие. В своих трудах они хотели представить музыку как некую математическую модель. Леонард Эйлер («Диссертация о звуке», 1727 г.) пишет: «Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке из правильных оснований всё, что может сделать приятным объединение и смешивание звуков». Об отношении к математике и музыке ученые высказывались в своих личных переписках. Лейбниц в письме Гольдбаху пишет: "Музыка есть скрытое арифметическое упражнение души, не умеющей считать". На что Гольдбах ему отвечает: "Музыка - это проявление скрытой математики".
Слова мелодия, ритм родились в Элладе, название слова «гамма» происходит от греческой буквы (гамма). После создания точной математической теории струны, поняв, что любой музыкальный инструмент – всего-навсего «физико-акустический прибор», музыку уже не отделить от математики. Математическому анализу подлежат и звук, и тембр, и лад, и гармония. Пифагор создал математическую теорию музыки, слушая, как звучат медные чаши. Каждое настоящее искусство имеет свою теорию, которую можно выразить в терминах математики. Математики, начиная с Пифагора, постоянно проявляли интерес к музыке.
Именно Пифагор был первым, кто попытался выразить красоту музыки с помощью чисел. Он создал свою школу мудрости, положив в ее основу два предмета – музыку и математику. Музыка, как одно из видов искусств, воспринималась наряду с арифметикой, геометрией и астрономией как научная дисциплина, а не как практическое занятие искусством.
Пифагор считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Он был не только философом, но и математиком, и теоретиком музыки. Пифагор основал науку о гармонии сфер, утвердив ее, как точную науку. Известно, что пифагорейцы пользовались специальными мелодиями против ярости и гнева.
Математическая модель музыкальных произведений.
Со времен Пифагора ученые делали попытки представить музыку в виде цифр. В нашей работе мы тоже попытались это сделать. Для исследования мы выбрали классические произведения и песенку Кота Леопольда из мультфильма, так как с этими произведениями мы познакомились на занятиях в музыкальной школе. Существует несколько способов представления звуков в форме математической модели. Если не учитывать длительность звучания нот, то сами ноты можно обозначать цифрами от 0 до 11: 0 – до, 1 – до#, 2 – ре, 3 – ре#, 4 – ми, 5 – фа, 6 – фа#, 7 – соль, 8 – соль#, 9 – ля, 10 – ля#, 11 – си (Приложение 2). Попробуем составить математическую модель произведения С. Рахманинова «Итальянская полька». Переложим ноты в первых шести тактах на цифры и получим такой ряд чисел: 490/44540/244/445411/044/9999. Черта между цифрами служит тактовой чертой, то есть делит на такты, как это сделано в произведении. В музыке есть понятие – устойчивые ступени, на которых строится тоническое звучание (Т5/3): 1, 3, 5 ступени (до, ми, соль). Сложим в каждом такте номера устойчивых ступеней. Получим ряд чисел: 4, 12, 8, 12, 4, 0 – кратных четырем (тактовый размер польки 2/4). Попробуем в каждом такте перемножить номера нот: I – 0 (4 * 9 * 0) II – 0 (4 * 4 * 5 * 4 * 0) III – 32 (2 * 4 * 4) IV – 3520 (4 * 4 * 5 * 4 * 11) V – 0 (0 * 4 * 4) VI – 6561 (9 * 9 * 9 * 9) Получили, что результаты в I, II и V тактах совпадают, в первых пяти тактах результаты кратны 4. Вот какая модель получилась у песенки кота Леопольда «Неприятность эту мы переживем». Получившийся ряд чисел: 407/407/0245/42/2117/2457/54/. Сложив в каждом такте номера нот устойчивых ступеней, получили ряд чисел: 11, 11, 4, 4, 7, 7, 11, 4 (повторяются три числа 11, 4 и 7). Перемножим в каждом такте номера нот: I – 0 (4 * 0 * 7) II – 0 (4 * 0 * 7) III – 0 (0 * 2 * 4 * 5) IV – 8 (4 * 2) 9 V – 154 (2 * 11 * 7) VI – 280 (2 * 4 * 5 * 7) VII – 20 (5 * 4) Все результаты произведения кратны двум (тактовый размер музыкального произведения 2/4). В некоторых интернет-источниках предлагается ещё один способ представления нот в виде цифр. Каждой ноте присваивается номер ступени: 1 – I ступень, 2 – II, 3 – III, 4 – IV, 5 – V, 6 – VI, 7 – VII, 8 – I, 9 – II, 0 – III. Переложим ноты музыкального произведения «Менуэт соль мажор» С. Баха на цифры. Возьмем первые 8 тактов. Получим следующий ряд: 95678/955/087890/55/8789876/78765/45675/76. Сложим в тактах номера устойчивых ступеней (1, 3 и 5) и увидим следующую последовательность чисел: 5, 10, 0, 10, 0, 5, 10, 0 – повторяются числа 5, 10 и 0. Используя этот же самый метод, представим в виде цифр произведение «Менуэт соль минор» С. Баха. Возьмем последние 8 тактов и получим следующий ряд: 5989/5090/594857/6/234567/876/7678954/5. Сложим в тактах номера устойчивых ступеней и увидим следующую последовательность чисел: 5, 5, 10, 0, 8, 0, 5, 5. Наблюдаем такую же закономерность, что и в предыдущем произведении. Представление музыкального произведения в виде числового ряда часто используют для обучения игре на музыкальном инструменте, и каждый автор предлагает свой способ кодирования нот .
Таким образом, любое музыкальное произведение можно представить как математическую модель, которая будет иметь числовые закономерностиВ пифагорийской школе проводили занятия математики под музыку, так как заметили, что она благотворно влияет на интеллект. Пифагор учился музыки в Египте и сделал ее предметом науки . Одним из достижений Пифагора и его последователей в математической теории музыки был разработанный ими «Пифагоров строй». Новая технология использовалась для настройки популярного в то время инструмента – лиры. Тем не менее, «Пифагоров строй» был несовершенен, как и древнегреческая арифметика. Расстояние между соседними звуками «Пифагорова строя» неодинаковые. Он – неравномерный. Чтобы сыграть мелодию, от какой- либо другой ноты, лиру каждый раз нужно перенастраивать.
 Пифагор установил, что первый обертон звучит выше основного тона на одну октаву. Второй обертон звучит выше первого на квинту; третий – выше второго на кварту; четвертый выше третьего на большую терцию. Потом пойдут малые терции, затем большие и малые секунды. Вот как выглядит обертоновый ряд от ноты
Пифагор установил, что первый обертон звучит выше основного тона на одну октаву. Второй обертон звучит выше первого на квинту; третий – выше второго на кварту; четвертый выше третьего на большую терцию. Потом пойдут малые терции, затем большие и малые секунды. Вот как выглядит обертоновый ряд от ноты
Вклад Пифагора
Еще в Древней Греции математика и музыка шли бок о бок и считались сестрами. Со времен Пифагора (570-490 гг. до н.э.) наука о музыке входила в пифагорейскую систему знаний, вместе с арифметикой, геометрией и астрономией.
С помощью математической формулы, Пифагор выяснил, какие пропорции существуют между звуками и какие из них лучше сочетаются между собой. Также, он создал свой музыкальный строй – Пифагорейский строй.
Также, пифогорейцы вычислили «золотую пропорцию» — конкретное место в музыкальном произведении, где должна быть кульминация.
Как в математике существует понятие скорости, так и в музыке темп, обозначает скорость музыкального движения. А длительности нот можно сравнить с математическим понятием целых чисел и дробей.
Музыканты прекрасно понимают какая связь существует между музыкой и математикой. Но человеку непосвященному, может показаться, что это совсем разные вещи. Музыка – творчество, а математика – наука.
Гипотеза: Если прослушивать классическую музыку постоянно, то у ученика активизируется мышление, повышается скорость решения математических задач,он лучше сосредоточится перед уроком и выполнением домашнего задания и в целом это положительно отразится на его здоровье.
С чего начинается знакомство с музыкой? Конечно, со звуков! Но чтобы их повторить, нам придётся окунуться в мир странных кружочков, палочек, крючочков и галочек, которые все вместе и будут составлять нотную грамоту. Оказывается, любую музыку можно записать с помощью семи нот, расставляя около них музыкальные знаки (аналогично в математике: десять цифр и знаки действия с ними). Ноты и паузы бывают целые, половинные, четвертные, восьмые, шестнадцатые и т.д., их связывает между собой математическая закономерность. Музыкальное произведение записывается при помощи нот не хаотично, а весь текст делится на такты, при этом все такты одного произведения имеют один размер, который и указывается в начале любого произведения. Например : ¾ будет означать, что в каждом такте должно быть ровно три четвертных ноты. При этом четвертные ноты могут разбиваться на восьмые, шестнадцатые или паузы того же размера. Расстояние между нотами (интервалы) также имеют свои названия и соответствуют определенному количеству тонов. Аккорды, которые сопровождают и украшают музыкальное произведение, высчитываются математическим путем и состоят из интервалов. Это относительно записи и чтения музыкальных произведений, но посмотрим на музыку с другой стороны.
Всякий звук - это воспринимаемые человеческим ухом колебания среды, обычно воздуха. Источником колебаний могут быть голосовые связки певца, струна музыкального инструмента, плохо смазанная дверь и т.п. Одна из основных характеристик колебательного процесса - частота колебаний. Особенность музыкальных звуков в определенной частоте колебаний. Когда говорят о частоте колебаний, определяющей ту или иную ноту, обычно употребляют термин высота звука. Ощущение высоты - это психологическая форма восприятия частоты колебаний звучащего тела, и чем больше частота колебаний, тем выше кажется звук и наоборот.
Человеческое ухо воспринимает звук, частота которого заключена приблизительно в интервале от 16 до 16000 Гц. В музыке используется диапазон от 16 до примерно 5000 Гц. Если считать только звуки с целым значением частоты, то получится около 5 тысяч. Между тем, концертный рояль - инструмент с огромным звуковым диапазоном - имеет всего 87 клавиш. Более того, через каждые двенадцать клавиш (семь белых и пять черных) повторяется их расположение и их названия. И очень высокие и очень низкие звуки носят одни и те же повторяющиеся имена: до, фа-диез, ля-бемоль и т.д. Постараемся понять, каким образом из всего многообразия звуков были отобраны именно те, к которым мы привыкли, и почему именно через каждые 12 клавиш повторяются названия нот. Для начала займемся измерениями. А где измерения, там вступает в свои права математика.
Каждая нота имеет определенную частоту и эту частоту можно вычислить с помощью формулы:
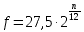 Гц
Гц
где n — это порядковый номер ступени (на клавиатуре номер клавиши слева), начиная с «ля» субконтроктавы, отсчитывается с нуля.
Например, для нахождения частоты «ре» малой октавы n будет равно 29:
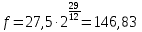 Гц
Гц
Таким образом, для каждой ноты вычисляется его частота. Раз уж звуки различаются по высоте, то естественно задать вопрос: "Насколько один звук выше другого?". И на этот вопрос удалось ответить с помощью математических вычислений. Рассмотрим отношения нескольких пар звуков. На слух звук с частотой 97,999 Гц настолько же выше звука с частотой 65,406 Гц, насколько звук в 783,99 Гц выше звука в 523,25 Гц. Во всех случаях мы имеем: отношение для каждой пары одно и то же и равно 3/2. Таким образом, отношение частот звука любой ноты к ноте до в любой октаве одинаковое. Расстояние между нотами, определяемое отношением их частот, называется интервалом. Некоторые, наиболее важные в музыке интервалы получили свои собственные имена. Так, отношение частот 3/2 определяет интервал квинты, а интервал октавы - образуют две ноты с отношением частот 2. Две одинаковые по высоте ноты относятся друг к другу с коэффициентом 1 и образуют интервал примы.
Интервалы имеют направление и могут определять движение как вверх, так и вниз (сравнимо с координатной прямой в математике). Переход от ноты с частотой ω к ноте с частотой 2ω дает октаву вверх, к ноте с частотой 2ω/3 - квинту вниз.
Чем же важен интервал октавы? Пусть наш исходный звук - нота до первой октавы. Возьмем от нее октаву вверх и октаву вниз. На слух эти три звука очень похожи, практически сливаются в одно целое. Поэтому обе получившиеся ноты также называются до, только расположены они в других октавах. Таким образом, частоты любых двух одноименных нот относятся друг к другу как некоторая степень числа 2.
Математическое описание этого явления было дано значительно позже усилиями д'Аламбера, Эйлера, Даниила Бернулли, Лагранжа. Такие выдающиеся имена не оставляют сомнений о важной роли математики в музыке, при этом не стоит забывать о важной особенности музыкально-математических исследований: результаты применения численных методов все время должны проверяться человеческим ухом.
Восприятие математики и музыки
Сегодня вряд ли кто-нибудь решится сводить музыку к определенным числовым действиям. Очевидно, надо начать с другого. Окружающий нас мир кроме звуков наполнен еще и ритмами. О чем говорит это слово? Посмотрите вокруг: ритмично звучат шаги, ритмичен ход часов, ритмично биение пульса человека, ритмично наше дыхание и т.д. И стоит нам услышать слово «ритм», как наши мысли невольно обращаются к музыке. И это понятно: ведь ритм – один из важнейших элементов музыки. На уроке сольфеджио обычно при изучении произведения «прохлопывают » ритм. Ритм в музыке - это сочетание размера и темпа. Если с темпом всё понятно, это «скорость» музыки, то размер представляет собой количество базовых длин звуков или пауз на один такт. Каким образом мы обычно считаем ритм музыки? Например, в вальсе чаще всего это повторение «раз-два-три, раз-два-три» — это есть ритм вальса, при этом каждая цифра означает долю, то есть составную часть одного такта. В приведённую фразу как раз помещается два такта, в каждом по три доли. В музыке под долей обычно имеется в виду одна четвертная нота, но возможны и другие варианты. В примере с классическим размером вальса это обычно три четверти, то есть в одном такте помещается ровно три равные длительности, которые, в свою очередь, могут быть разбиты на более мелкие по длительности звуки или объединены в более длинные.
В музыке мы имеем дело с короткими и длинными длительностями, они составляют основу любого ритма: целая нота, половинная, одна четверная, одна восьмая, одна шестнадцатая. Названия длительности служат одновременно и названиями чисел. Нетрудно понять, почему длительности музыкальных нот заимствовали свои названия у дробей. Мы видим, что длительности получаются так же, как дроби: они возникают при делении целой ноты на равные доли. Поэтому длительность можно подсчитывать как дробные числа, например:
 +
+ =
= 
Равенство здесь надо понимать в том смысле, что длительность слева равна сумме длительностей справа. С помощью чисел то же равенство можно записать в виде 1/4 = 1/8 + 2/10
 +
+  +
+  = 1/1 = 1/4 + 1/4 + 1/2 и т.д.
= 1/1 = 1/4 + 1/4 + 1/2 и т.д.
Если все длительности в музыкальном произведении увеличить вдвое, произведение надо исполнять медленнее и наоборот.
Исследование дат рождений и имен.
Математическая чистота звука
Первым, кто в построении теории музыки отдавал приоритет слуховым ощущениям, был ученик Аристотеля Аристоксен. Основателем школы, ставившей во главу угла математические соотношения, был Пифагор. Его же признают создателем первой музыкальной теории.
Для своих исследований Пифагор использовал так называемый монохорд (в переводе с греческого - однострунный). Инструмент представлял собой четырехугольный ящик длиной около 1 метра, над верхней декой (доской) располагалась одна струна, ограниченная с двух сторон порожками. Под струной располагалась двигающаяся подставка, которая позволяла изменять высоту звука.
Вообще говоря, высота звука, издаваемого струной, определяется несколькими параметрами - длиной и толщиной струны, плотностью материала, из которого она изготовлена, натяжением и т.д. Когда свойства звука изучаются на монохорде, то толщина струны, ее натяжение и плотность материала остаются неизменными. Высота извлекаемого звука изменяется простым смещением подставки.
Частота, с которой колеблется вся струна целиком, определяет так называемый основной тон. Колебания частей струны вызывают появление обертонов. Самые сильный обертон возникает при колебаниях 1/2 части струны, слабее 1/3, 1/4, 1/5 и т.д. Соответственно соотношение частот (или высот) этих обертонов выглядит так: 1:2:3:4:5:6... Это так называемый натуральный или гармонический ряд звуков, и соответствующие обертоны тоже называются гармоническими. Попытаемся установить связь между датой рождения, нумерологического анализа имени и фамилии человека с музыкой, предварительно присвоив каждой ноте номер ступени: до – 0, ре – 1, ми – 2, фа – 3, соль – 4, ля – 5, си – 6, до – 7, ре – 8, ми – 9. Переложим даты рождений (двумя способами) учащихся и имена и фамилии на ноты. У каждого человека получилось три аккорда. Если аккорд звучит гармонично – то ставим (+), в музыке это звучание называется консонанс, если аккорды звучат негармонично – то (-), в музыке это звучание называется диссонанс. И проведем сравнительный анализ между звучанием аккордов и увлечениями и особенностями характера ребят.
| Ф.И.О. | Дата рождения | Аккорд | Благозвучие | Увлечение | Соответст-вие |
| Видвичук Екатерина Владимировна | 20.02.2002 |  | Консонанс | Музыкальная школа (фортепиано), вокал, акробатика | Да |
| Кривуляк Виктория Михайловна | 14.05.2002 | 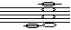 | Диссонанс | Рисование | Нет |
| Лёвкина Елизавета Юрьевна | 10.05.2002 | 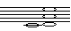 | Диссонанс | Рисование | Нет |
| Мужева Мария Станиславовна | 28.03.2003 | 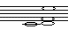 | Диссонанс | Музыкальная школа (саксофон), баскетбол | Нет |
| Пономарева Диана Романовна | 03.07.2002 | 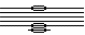 | Диссонанс | Интерес к физике, математике, химии | Да |
| Прородченко Мария Валерьевна | 21.03.2002 | 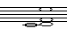 | Диссонанс | Рисование | Нет |
| Сабанова Екатерина Сергеевна | 28.10.2002 | 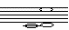 | Диссонанс | Вокал | Нет |
| Шилов Михаил Геннадьевич | 07.08.2002 | 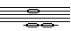 | Диссонанс | Рисование, сочинение стихов | Нет |
| Курочкина Арина Витальевна | 26.12.2002 | 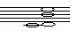 | Консонанс | Музыкальная школа (фортепиано) | Да |
| Петрушкина Анна Сергеевна | 13.07.2002 | 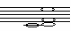 | Диссонанс | Музыкальная школа (скрипка) | Нет |