Файл: I. Роль тригонометрии в школьном курсе математики История развития тригонометрии.rtf
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 55
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Разумеется, вы должны четко знать стандартные формулы корней простейших тригонометрических уравнений (полезно помнить или уметь получать с помощью тригонометрической окружности упрощенные формулы для корней уравнений
Определение 1. Тригонометрическим уравнением называется уравнение, содержащее переменную под знаком тригонометрических функций.
Простейшие тригонометрические уравнения - это уравнения вида
В таких уравнениях переменная находится под знаком тригонометрической функции, а - данное число.
Каждое из таких уравнений решается по формулам, которые следует знать. Вот эти формулы:
Частные случаи
При решении тригонометрических уравнений все задачи сводятся к тому, чтобы привести к такому виду, чтобы слева стояла элементарная тригонометрическая функция, а справа - число. После того, как это будет достигнуто, следует найти значение аргумента функции, используя одну из основных формул выражения аргумента через обратные тригонометрические функции.
.4 Основные понятия и формулы тригонометрии
В тригонометрии угол рассматривается как мера вращения, при котором один луч, вращаясь вокруг вершины угла, переходит в положение другого луча. При этом первый луч называют начальной стороной угла, а конечное положение второго (подвижного) луча называют конечной стороной угла.
Угол считается положительным, если переход от его начальной стороны к конечной совершается вращением подвижного луча против часовой стрелки, и отрицательным, если такой переход совершается вращением по часовой стрелке.
Единичный круг - круг с центром в начале координат и радиусом, равным по длине единице. Окружность этого круга называется единичной окружностью.
Координатные оси делят единичный круг и его окружность на четыре равные части, которые называются четвертями, или квадрантами.
Синус - отношение ординаты конца подвижного радиуса к длине этого радиуса.
Косинус - отношение абсциссы конца подвижного радиуса к длине этого радиуса.
Тангенс - отношение ординаты конца подвижного радиуса к его абсциссе.
Котангенс - отношение абсциссы конца подвижного радиуса к его ординате.
Секанс - отношение длины подвижного радиуса к абсциссе его конца.
Косеканс - отношение длины подвижного радиуса к ординате его конца.
Линия тангенсов - касательная к единичной окружности в конце горизонтального диаметра.
Линия котангенсов - касательная к единичной окружности в конце вертикального диаметра.
Синус и косинус угла равны соответственно ординате и абсциссе конца подвижного радиуса единичной окружности.
Если продолжить единичный радиус до пересечения с линией тангенсов, то тангенс угла равен ординате соответствующей точки на линии котангенсов.
Если продолжить единичный радиус до пересечения с линией котангенсов, то котангенс угла равен абсциссе соответствующей точки на линии котангенсов.
Основные тригонометрические тождества
2 α + cos 2 α = 1
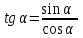
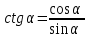
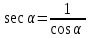
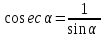
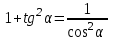
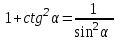
Тождественные преобразования тригонометрических выражений
Функция y = f (x) называется четной, если значение y не изменяется при замене x на -x, т.е. функция y = f (x) называется четной, если f (-x) = f (x)
Функции cos α, sec α, - четные функции, а sin α, tg α, ctg α cosec α - нечетные.
Теоремы сложения: позволяют, зная значения тригонометрических функций двух аргументов α и β, вычислять значения тригонометрических функций от суммы (α + β) и разности (α - β) этих аргументов.
Формулы сложения
sin (α + β) = sin α ∙ cos β + cos α ∙ sin β (α - β) = sin α ∙ cos β - cos α ∙ sin β (α + β) = cos α ∙ cos β - sin α ∙ sin β (α - β) = cos α ∙ cos β + sin α ∙ sin β
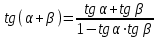
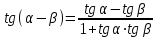
Формулы приведения
Формулы, при помощи которых тригонометрические функции произвольного угла можно выразить через тригонометрические функции острого угла, называются формулами приведения.
Формулы удвоения и деления аргумента
sin 2α = 2 sin α ∙ cos α
cos 2α = cos 2 α - sin 2 α
2 cos 2α = 1 + cos 2 α
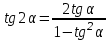
Формулы преобразования произведения тригонометрических функций в сумму
2 cos α ∙ cos β = cos (α - β) + cos (α + β)
sin α ∙ sin β = cos (α - β) - cos (α + β)
sin α ∙ cos β = sin (α + β) + sin (α - β)
.5 Решение тригонометрических уравнений
Поскольку каждому значению тригонометрической функции соответствует неограниченное множество углов, то тригонометрическое уравнение, если не сделано каких-либо оговорок, имеет бесчисленное множество решений.
Самый общий метод решения тригонометрических уравнений состоит в том, что различные тригонометрические функции, входящие в уравнение, выражают через какую-нибудь одну из них и, принимая функцию за неизвестное, решают полученное алгебраическое уравнение, в результате чего приходят к одному из так называемых простейших тригонометрических уравнений вида:
sin x = a x = b
tg x = c x = d
где a, b, c, d - числа. a - угол, содержащийся в промежутке от - π/2 до π/2, синус которого равен a. b - угол, содержащийся в промежутке от 0 до π, косинус которого равен b. c - угол, содержащийся в промежутке от - π/2 до π/2, тангенс которого равен c. d - угол, содержащийся в промежутке от 0 до π, котангенс которого равен d.
Решение произвольного тригонометрического уравнения, как правило, сводится к решению одного или нескольких простейших уравнений. Одной из основных идей решения является идея, общая для всех типов уравнений,- переход от одного уравнения к уравнению-следствию или равносильному уравнению (или их системе либо совокупности), от него к следующему и т. д., пока не придем к простейшим уравнениям, из которых получаем решение исходного уравнения. При переходе используются как общие методы (пригодные для любого типа уравнений), так и частные, основанные на использовании формул тождественных преобразований тригонометрических выражений.
.6 Рекомендации по решению тригонометрических уравнений
1. Если аргументы функций одинаковые, попробовать получить одинаковые функции, использовав формулы без изменения аргументов.
2. Если аргументы функций отличаются в два раза, попробовать получить одинаковые аргументы, использовав формулы двойного аргумента.
. Если аргументы функций отличаются в четыре раза, попробовать их привести к промежуточному двойному аргументу.
. Если есть функции одного аргумента, степени свыше первой, попробовать понизить степень, используя формулы понижения степени или формулы сокращенного умножения. Например,
5.
Если есть сумма одноименных функций первой степени с разными аргументами (вне случаев 2,3), попробовать преобразовать сумму в произведение для появления общего множителя.
6. Если есть сумма разноимённых функций первой степени с разными аргументами (вне случаев 2, 3), попробовать использовать формулы приведения, получить затем случай 5.
. Если в уравнении есть произведение косинусов (синусов) различных аргументов, попробовать свести его к формуле синус двойного аргумента, умножив и разделив это выражение на синус (косинус) подходящего аргумента: