11 AB=BA Переместительное тождество для логического произведения

12 A(B+C)=AB+AC Распределительное тождество

13 (A+B)(A+C)=BC+A Распределительное тождество

14 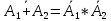·Соотношение двойственности (теорема де Моргана)

15 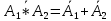Соотношение двойственности (теорема де Моргана)

Доказательство основных тождеств может быть проведено разными способами, например, сравнением таблиц истинности для левой и правой части каждого тождества.

Особого внимания заслуживают тождества 13-15, не имеющие аналогии в обычной алгебре. Ввиду того, что в схемотехнике широко используются операции НЕ-ИЛИ (отрицание логического сложения) и НЕ-И (отрицание логического умножения), тождества 14 и 15 можно доказать с помощью таблиц истинности.

Логические функции могут иметь формы представления: 1) словесное, 2) графическое, 3) табличное, 4) алгебраическое, 5) на алгоритмическом языке (например VHDL) и 6) схемное.

Пример таблицы истинности логической функции:

X1	X2	X3	Y
0	0	0	1
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

Восстановление алгебраической функции по таблице истинности. В дизъюктивной функции складываются произведения тех значений на входе, которые на выходе дают 1, причем, если на входе значение 0, то добавляются в инверсном виде:

__ __ __ __ __ __ __ __

Y=X1*X2*X3+ X1*X2*X3+ X1*X2*X3+ X1*X2*X3 = X1*X2 + X1*X2

Карты Карно (табличное упрощение): - в двух соседних по горизонтали и вертикали клетках отличается значение только одного аргумента

	X1X2
X3X4	00	01	11	10
00	1			1
01	1			1
11		1	1
10		1	1

---

Объединяются области (импликанты) по 2*i ячеек, можно объединять по горизонтали первый и последний столбец. При сокращении записывается сумма импликантов (прямоугольников), причем записывается произведение тех аргументов, которые в соседних клетках не изменяют своего значения.

Y= X2*X3 + X2*X3

Выражение можно преобразовать к базису И-НЕ (по т. Де Моргана через 2 инвертора):

Y= ((X2*X3) + (X2*X3)) =  ( (X2*X3) * (X2*X3))

Работа в TinkerCAD

Задание упростить таблицу истинности и реализовать схему по заданию преподавателя в Tinkercad. Пример

X1	X2	X3	Y		X1X2
0	0	0	1	X3	00	01	11	10
0	0	1	0	0	1	1	1
0	1	0	1	1		1		1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

---

Y= (X1*X3)+(X1*X2*X3)+ (X1*X2*X3)= (X1*X3)+ X1*( X2*X3+*X2*X3)

Без упрощения -

Y= (X1*X2*X3)+ (X1*X2*X3) + (X1*X2*X3)+ (X1*X2*X3) +(X1*X2*X3)

Пример реализации и принципиальная схема Tinkercad -





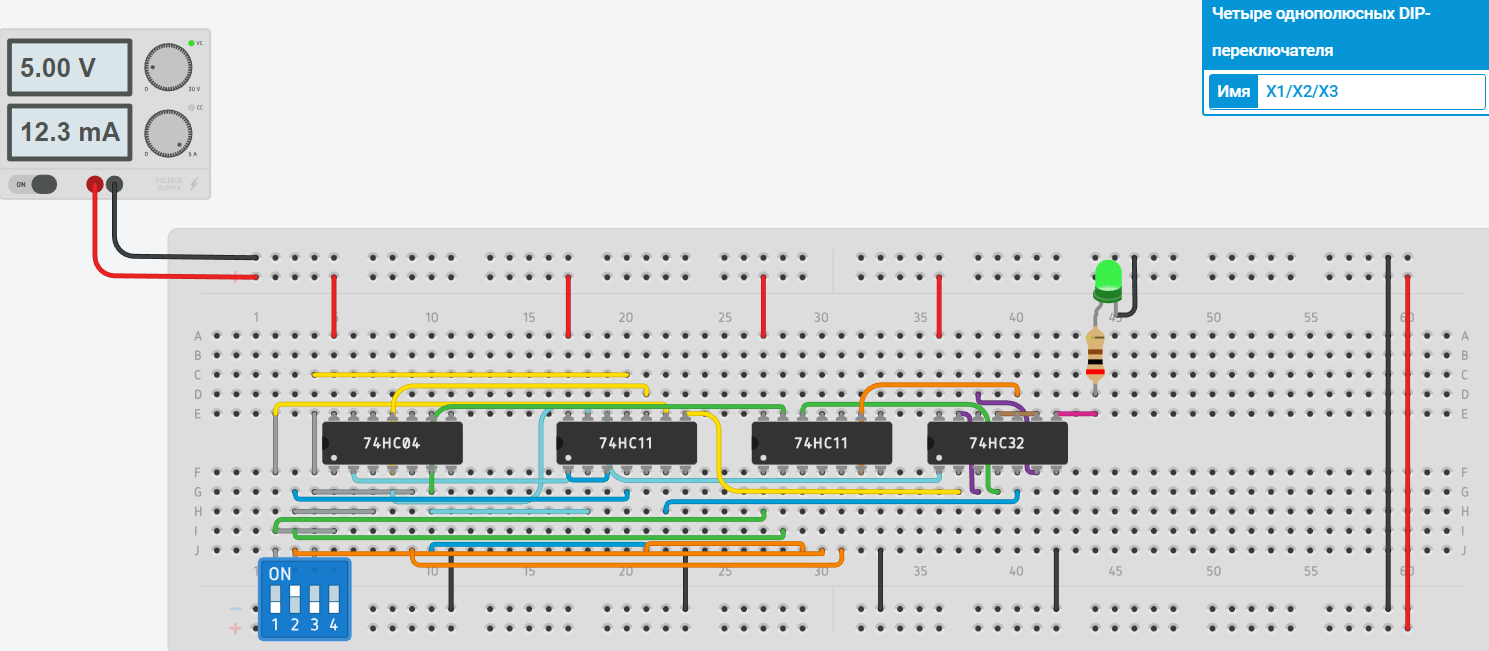
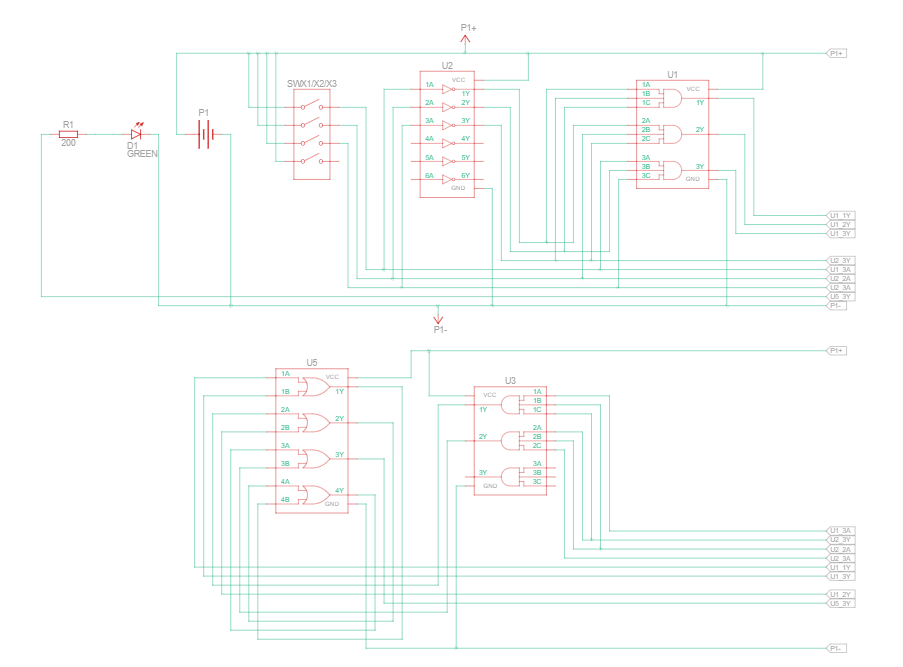
Список контрольных вопросов

1.Как проводится испытание схем в статическом режиме? Какие сигналы подавать на вход и как контролировать выходные сигналы?

2. Как определить неисправность схемы?

3. Как производится испытание схем в динамическом режиме? Какие сигналы подавать на вход, как контролировать входные сигналы?

4. Какие тождества булевой алгебры Вы знаете?

5. Докажите основные тождества булевой алгебры.

---

Лабораторная работа 3. Проверка таблицы истинности D и RS триггеров

Цель работы:

• Ознакомиться с назначением и принципом действия триггеров

• Ознакомиться с практическими схемами RS, D и JK триггеров и исследовать их.

Теоретическое введение:

Триггер – это логическая схема с положительной обратной связью, имеющая два устойчивых состояния, которые называются единичным и нулевым и обозначаются 1 и 0. Перевод триггера в единичное состояние производится путем воздействия на его вход и называется установкой (set) триггера. Устанавливающий сигнал и вход на который он воздействует обозначают S. Перевод триггера в нулевое состояние называют сбросом (reset), а соответствующий вход и сигнал обозначают R.

Схема простейшего триггера получается, если включить кольцом два элемента ИЛИ – НЕ. Такой триггер имеет два входа R и S, два выхода Q и Q и называется RS триггером. Его обозначение на функциональных схемах показано на рисунке 3а.

RS триггер – простейший тип бистабильного асинхронного триггера

(R-reset, S-set, Q- выходное значение триггера, Q-инвертированное значение выхода)

R	S	Q(t)	Q(t+1)	Пояснения
0	0	0	0	Режим хранения информации R=S=0
0	0	1	1
0	1	0	1	Режим установки единицы S=1
0	1	1	1
1	0	0	0	Режим записи нуля R=1
1	0	1	0
1	1	0	*	R=S=1 запрещенная комбинация
1	1	1	*

---

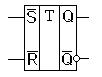
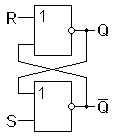
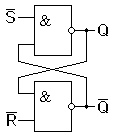
Рис. 3а Схема RS на ИЛИ-НЕ Таблица истинности RS триггера

С	R	S	Q(t)	Q(t+1)	Пояснения
0	x	x	0	0	Режим хранения информации
0	x	x	1	1
1	0	0	0	0	Режим хранения информации
1	0	0	1	1
1	0	1	0	1	Режим установки единицы S=1
1	0	1	1	1
1	1	0	0	0	Режим записи нуля R=1
1	1	0	1	0
1	1	1	0	*	R=S=1 запрещенная комбинация
1	1	1	1	*

---

Смотрите также файлы

• Отчет по лабораторной работе 3 По дисциплине Химия (наименование учебной дисциплины, согласно учебному плану).docx

• Московская международная академия.docx

• Износостойкие сопла для распыления абразивных суспензий.pdf

• Туляремия.docx

• Лицо привлечено к уголовной ответственности за незаконную предпринимательскую деятельность при сдаче в аренду жилого помещения третьим лицам без регистрации в качестве индивидуального предпринимателя.docx