Файл: Лабораторная работа Базовые логические операции и, или, не.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 125
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Счетчиком называют устройство, сигналы на выходе которого в определенном коде отображают число импульсов, поступивших на счетный вход. Счетчик, образованный цепочкой из m триггеров может подсчитать в двоичном коде К сч = 2 m импульсов. Каждый из этих триггеров называется разрядом счетчика. Число К сч , равное числу различных состояний на выходах триггеров счетчика, называется модулем счета. Число входных импульсов и состояние счетчика взаимно определены только для первого цикла, так как после того как число входных импульсов превысит К сч , счетчик возвращается в нулевое состояние и повторяется цикл работы.
Цифровые счетчики классифицируются следующим образом:
по модулю счета:
двоичные, двоично-десятичные, с произвольным модулем счета;
по направлению счета:
суммирующие, вычитающие, реверсивные;
по способу организации внутренних связей:
с последовательным переносом, с параллельным переносом, с комбинированным переносом, кольцевые.
Классификационные признаки независимы и могут встречаться в различных сочетаниях.
При построении суммирующего счетчика с последовательным переносом на Т – триггерах необходимо соединить прямой выход последующего триггера со входом последующего триггера (рисунок 6).
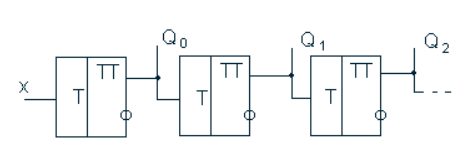
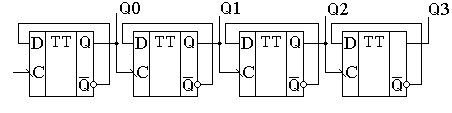
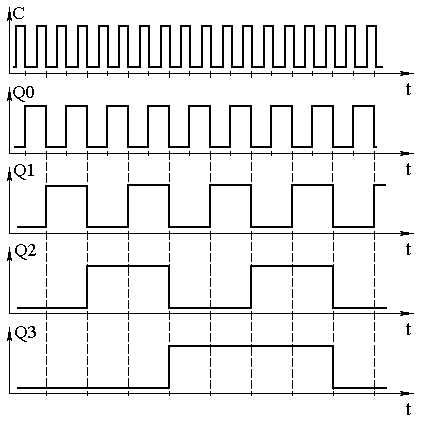
Рис. 6 Суммирующий счетчик с последовательным переносом.
При построении вычитающего счетчика с последовательным переносом, необходимо соединить инверсный выход предыдущего со входом последующего триггера (рисунок 7):
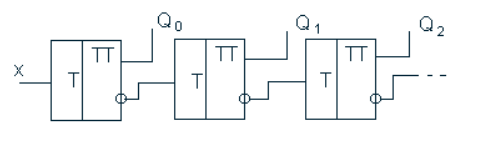
Рис. 7 Вычитающий счетчик с последовательным переносом.
Задача каждого триггера в 2 системе делить частоту импульсов на 2. Срабатывание происходит по заднему фронту импульса на С (при переходе от 1 к 0).
Параллельные счетчики (синхронные с параллельным переносом) имеют максимальное быстродействие, поскольку в них все разряды переключаются одновременно.
Параллельный счетчик содержит разрядные триггеры с конъюнкторами
, анализирующими состояния предыдущих разрядов. При поступлении входного сигнала переключаются только те триггеры, для которых все предыдущие были единичном состоянии, что и требуется. Время установления счетчика не зависит от разрядности и равно
t к = t з.к + t тг ,
где t з.к – задержка сигнала конъюнктором.
Трудности реализации многоразрядных параллельных счетчиков связаны с ростом числа входов у конъюнкторов (или числа входов J и K в триггерах) по мере увеличения разрядности счетчика. Второй ограничивающий фактор – рост нагрузки на выходы триггеров по мере увеличения числа разрядов счетчика. Применение различных схем буферного типа для преодоления указанных ограничений обычно нежелательно, так как снижает быстродействие счетчика.
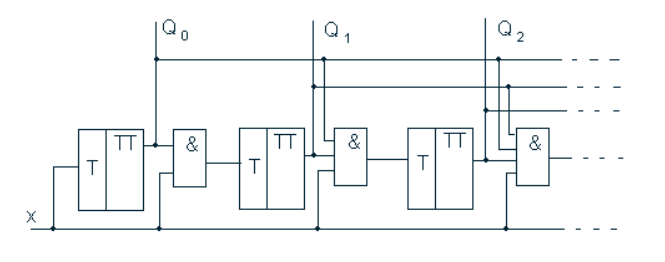
Рис. 8 Схема параллельного счетчика
В параллельных счетчиках все разряды переключаются одновременно,
поэтому их структуре свойственны временные состязания сигналов (рисунок 8). При использовании двухступенчатых триггеров состязания исключаются.
Реверсивные счетчики изменяют направление счета под воздействием управляющего сигнала или при смене точки подачи считаемых сигналов (рисунок 9). В первом случае схема имеет счетный и управляющий входы, во втором – два счетных входа.
Наиболее распространенный способ построения реверсивных счетчиков – переключение межразрядных связей. Если управляющий сигнал перестраивает межразрядные связи, перенося точку съема сигнала с одного выхода триггера на другой, то реализуется схема реверсивного счетчика.
Последовательный счетчик преобразуется в реверсивный путем введения в его структуру элементов реверса. В связи с появлением дополнительных задержек введение реверса снижает быстродействие счетчика.
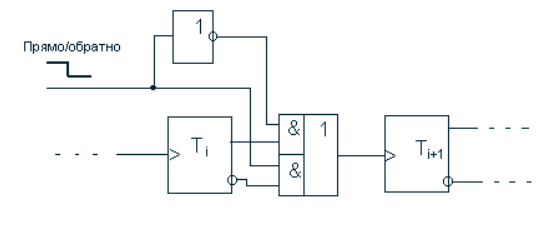
Рис. 9 Схема реверсивного счетчика.
Синхронный счетчик на JK триггерах
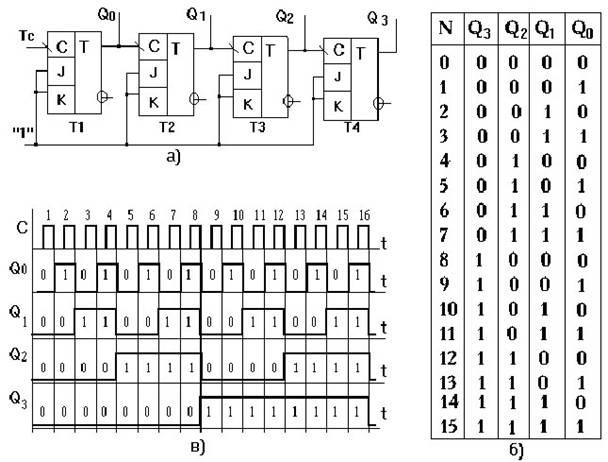
Для реализации счетчика на JKтриггере (74HC74) на сброс нужно R подать питание 5В.
https://pdf1.alldatasheetru.com/datasheet-pdf/view/532360/NXP/74HC74.html
Работа в Nandgame


Необходимо выполнить задания «Счётчик» и «Регистр» уровня «Memory».
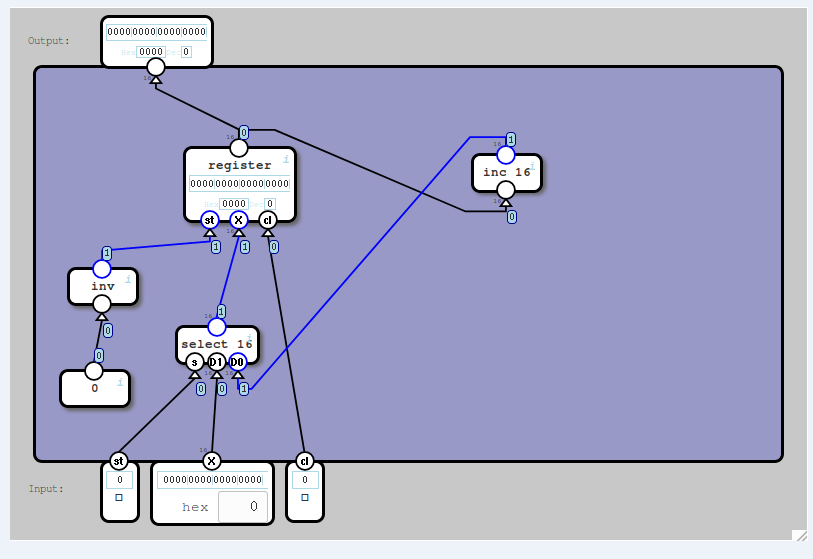
Работа в TinkerCAD
Пользуясь доступными микросхемами 74HC73, реализовать счетчик на JK триггерах.
Протестировать его работу.
Пример реализации счетчика в Tinkercad на JK триггерах
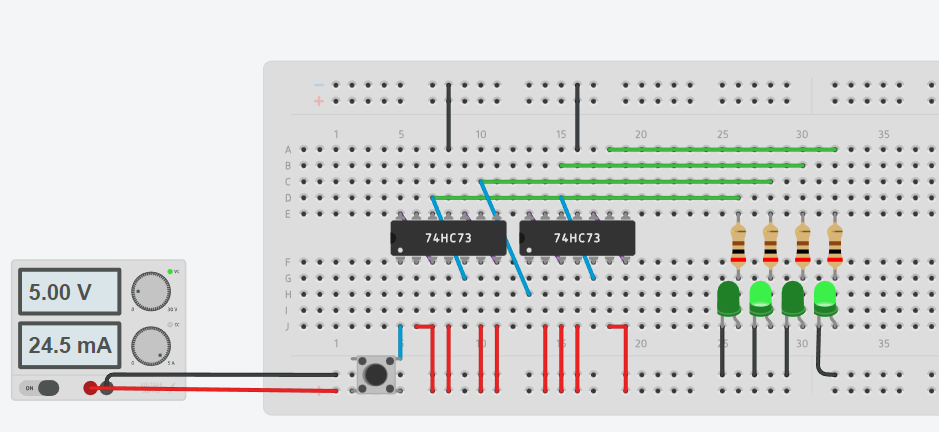
Список контрольных вопросов
1. Нарисуйте принципиальную электрическую схему счетчика;
2. Покажите временные диаграммы работы счетчика.
Лабораторная работа 5. Полусумматор и сумматор (арифметика)
Цель работы:
• Ознакомится с назначением и принципом действия сумматоров
• Ознакомится с практической схемой сумматора и исследовать её
Теоретическое введенеие
Сумматоры представляют собой функциональные узлы, выполняющие операцию сложения чисел. В устройствах дискретной техники суммирование осуществляется в двоичном или, реже, в двоично-десятичном коде. По характеру действия сумматоры подразделяются на две категории :
комбинационные – как и все ранее рассмотренные узлы, не имеющие элементов памяти ; накопительные – сохраняющие результаты вычислений.
В свою очередь, каждый из сумматоров, оперирующий с многоразрядными слагаемыми, в зависимости от способа обработки чисел может быть отнесен к последовательному или параллельному типу. Сумматоры, выполненные в виде самостоятельных микросхем – комбинационные, и речь в дальнейшем будет идти только о них.
Как последовательные, так и параллельные сумматоры строятся на основе одноразрядных суммирующих схем. Сложение чисел в последовательных сумматорах осуществляется поразрядно, последовательно во времени. В сумматорах параллельного типа действия сложение всех разрядов много разрядных чисел происходит одновременно.
Двоичный сумматор –является основным блоком процессора. При сравнении процессоров наиболее важной характеристикой является разрядность сумматора.
Все сумматоры делятся на:
Сумматор по модулю 2 - суммирование без учета переноса (исключающее ИЛИ)
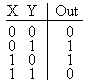
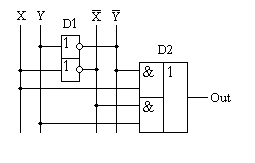
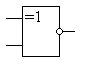
Полусумматор – учитывает запоминает последующий перенос, но не учитывает перенос предыдущего разряда
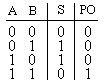
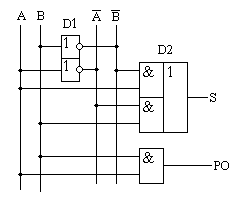
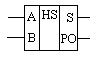
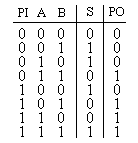
Полный двоичный одноразрядный сумматор
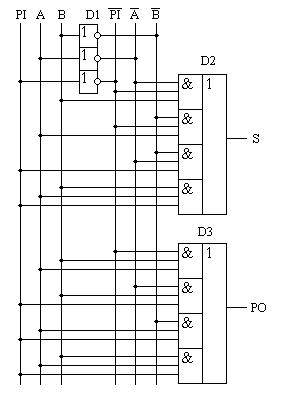
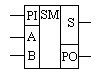
Многоразрядный сумматор – соединение двоичных сумматоров
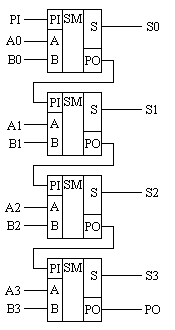
Рассмотрим их подробннее.
Полусумматор.
Простейшим суммирующим элементом является полусумматор.
Происхождение этого термина станет ясным в ходе изложения. Он имеет (см. рис. ) два входа А и В для двух слагаемых и два выхода : S(сумма) и P(перенос).
Обозначением полусумматора служат буквы HS (HalfSum – полусумма), работу прибора отражает таблица истинности :
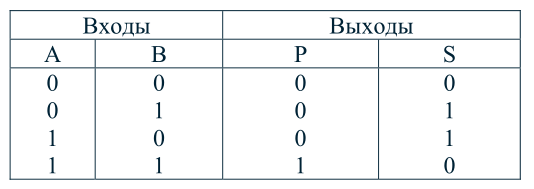
Полусумматор имеет два входа и пригоден для использования только в младших разряде. Устройство для суммирования многоразрядных чисел должно иметь, начиная со второго разряда, три входа : два для слагаемых Ai и Bi и один для сигнала переноса Pi-1 с предыдущего разряда. Этот узел – сумматор можно представить как объединение двух полусумматоров (рисунок 10):
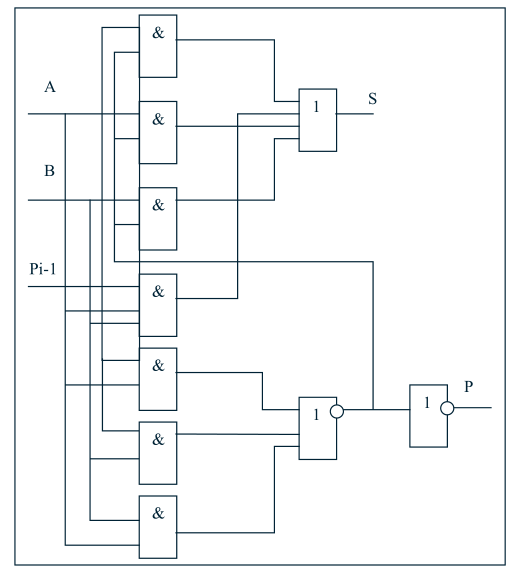
Рис. 10 Объединение двух полусумматоров
Первый полусумматор служит для сложения двух чисел, принадлежащих одному разряду, и обеспечивает выход промежуточной суммы Si и переноса Pi.
Второй полусумматор складывает перенос с предыдущего разряда Pi-1 с промежуточной суммой Si. Функции выходов S и P для этого случая определяется как
S=(A+B)+Pi-1; (9-3) Pi+1=AiBi ^ (A+B) Pi-1 (9-4)
Операции сложения подчиняется переносительному закону, из которого следует, что входы сумматора можно менять местами без ущерба для результата.
Исходя из таблицы истинности сумматора, можно написать следующие булевые уравнения для сигналов суммы и переноса
_ _ _ __ _ __
Si=AiBiPi-1 ^ AiBiPi-1 ^ AiBiPi-1 ^ AiBiPi-1
_ _ __
Pi=AiBiPi-1 ^ AiBiPi-1 ^ AiBiPi-1 ^ AiBiPi-1
В уравнениях представлены только те члены, для которых Si=1 и Pi=1, т.е. первый член функции Si относится к первой строке таблицы истинности, второй член ко второй и т.д. Сходным образом для функции P первый член принадлежит третей строке, второй- пятой и так до седьмой. Уравнения поддаются оптимизации, в результате которой получается
Цифровые счетчики классифицируются следующим образом:
по модулю счета:
двоичные, двоично-десятичные, с произвольным модулем счета;
по направлению счета:
суммирующие, вычитающие, реверсивные;
по способу организации внутренних связей:
с последовательным переносом, с параллельным переносом, с комбинированным переносом, кольцевые.
Классификационные признаки независимы и могут встречаться в различных сочетаниях.
При построении суммирующего счетчика с последовательным переносом на Т – триггерах необходимо соединить прямой выход последующего триггера со входом последующего триггера (рисунок 6).



Рис. 6 Суммирующий счетчик с последовательным переносом.
При построении вычитающего счетчика с последовательным переносом, необходимо соединить инверсный выход предыдущего со входом последующего триггера (рисунок 7):

Рис. 7 Вычитающий счетчик с последовательным переносом.
Задача каждого триггера в 2 системе делить частоту импульсов на 2. Срабатывание происходит по заднему фронту импульса на С (при переходе от 1 к 0).
Параллельные счетчики (синхронные с параллельным переносом) имеют максимальное быстродействие, поскольку в них все разряды переключаются одновременно.
Параллельный счетчик содержит разрядные триггеры с конъюнкторами
, анализирующими состояния предыдущих разрядов. При поступлении входного сигнала переключаются только те триггеры, для которых все предыдущие были единичном состоянии, что и требуется. Время установления счетчика не зависит от разрядности и равно
t к = t з.к + t тг ,
где t з.к – задержка сигнала конъюнктором.
Трудности реализации многоразрядных параллельных счетчиков связаны с ростом числа входов у конъюнкторов (или числа входов J и K в триггерах) по мере увеличения разрядности счетчика. Второй ограничивающий фактор – рост нагрузки на выходы триггеров по мере увеличения числа разрядов счетчика. Применение различных схем буферного типа для преодоления указанных ограничений обычно нежелательно, так как снижает быстродействие счетчика.

Рис. 8 Схема параллельного счетчика
В параллельных счетчиках все разряды переключаются одновременно,
поэтому их структуре свойственны временные состязания сигналов (рисунок 8). При использовании двухступенчатых триггеров состязания исключаются.
Реверсивные счетчики изменяют направление счета под воздействием управляющего сигнала или при смене точки подачи считаемых сигналов (рисунок 9). В первом случае схема имеет счетный и управляющий входы, во втором – два счетных входа.
Наиболее распространенный способ построения реверсивных счетчиков – переключение межразрядных связей. Если управляющий сигнал перестраивает межразрядные связи, перенося точку съема сигнала с одного выхода триггера на другой, то реализуется схема реверсивного счетчика.
Последовательный счетчик преобразуется в реверсивный путем введения в его структуру элементов реверса. В связи с появлением дополнительных задержек введение реверса снижает быстродействие счетчика.

Рис. 9 Схема реверсивного счетчика.
Синхронный счетчик на JK триггерах

Для реализации счетчика на JKтриггере (74HC74) на сброс нужно R подать питание 5В.
https://pdf1.alldatasheetru.com/datasheet-pdf/view/532360/NXP/74HC74.html
Работа в Nandgame
-
Зайти на сайт nandgame.com. -
При желании переключить интерфейс на русский.
-
Изучить интерфейс. Входы (input) в виде логических переменных, расположены снизу. Щелчком мыши по ним вы можете менять их состояние с 0 на 1 и обратно. Кроме них внизу находится блок питания (Power), он всегда выдает логическую единицу. -
Ознакомиться с заданием, которое представлено в текстовом виде. -
Изучить спецификацию, представленную в виде таблицы истинности логической функции. -
Реализовать функцию управления, согласно спецификации. Для реализации вам представлены логические элементы.
-
Проверить своё решение, нажав кнопку «Check solution», при возникновении ошибок – исправить их.

Необходимо выполнить задания «Счётчик» и «Регистр» уровня «Memory».

Работа в TinkerCAD
Пользуясь доступными микросхемами 74HC73, реализовать счетчик на JK триггерах.
Протестировать его работу.
Пример реализации счетчика в Tinkercad на JK триггерах

Список контрольных вопросов
1. Нарисуйте принципиальную электрическую схему счетчика;
2. Покажите временные диаграммы работы счетчика.
Лабораторная работа 5. Полусумматор и сумматор (арифметика)
Цель работы:
• Ознакомится с назначением и принципом действия сумматоров
• Ознакомится с практической схемой сумматора и исследовать её
Теоретическое введенеие
Сумматоры представляют собой функциональные узлы, выполняющие операцию сложения чисел. В устройствах дискретной техники суммирование осуществляется в двоичном или, реже, в двоично-десятичном коде. По характеру действия сумматоры подразделяются на две категории :
комбинационные – как и все ранее рассмотренные узлы, не имеющие элементов памяти ; накопительные – сохраняющие результаты вычислений.
В свою очередь, каждый из сумматоров, оперирующий с многоразрядными слагаемыми, в зависимости от способа обработки чисел может быть отнесен к последовательному или параллельному типу. Сумматоры, выполненные в виде самостоятельных микросхем – комбинационные, и речь в дальнейшем будет идти только о них.
Как последовательные, так и параллельные сумматоры строятся на основе одноразрядных суммирующих схем. Сложение чисел в последовательных сумматорах осуществляется поразрядно, последовательно во времени. В сумматорах параллельного типа действия сложение всех разрядов много разрядных чисел происходит одновременно.
Двоичный сумматор –является основным блоком процессора. При сравнении процессоров наиболее важной характеристикой является разрядность сумматора.
Все сумматоры делятся на:
Сумматор по модулю 2 - суммирование без учета переноса (исключающее ИЛИ)
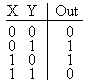

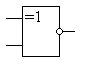
Полусумматор – учитывает запоминает последующий перенос, но не учитывает перенос предыдущего разряда



Полный двоичный одноразрядный сумматор



Многоразрядный сумматор – соединение двоичных сумматоров

Рассмотрим их подробннее.
Полусумматор.
Простейшим суммирующим элементом является полусумматор.
Происхождение этого термина станет ясным в ходе изложения. Он имеет (см. рис. ) два входа А и В для двух слагаемых и два выхода : S(сумма) и P(перенос).
Обозначением полусумматора служат буквы HS (HalfSum – полусумма), работу прибора отражает таблица истинности :

Полусумматор имеет два входа и пригоден для использования только в младших разряде. Устройство для суммирования многоразрядных чисел должно иметь, начиная со второго разряда, три входа : два для слагаемых Ai и Bi и один для сигнала переноса Pi-1 с предыдущего разряда. Этот узел – сумматор можно представить как объединение двух полусумматоров (рисунок 10):

Рис. 10 Объединение двух полусумматоров
Первый полусумматор служит для сложения двух чисел, принадлежащих одному разряду, и обеспечивает выход промежуточной суммы Si и переноса Pi.
Второй полусумматор складывает перенос с предыдущего разряда Pi-1 с промежуточной суммой Si. Функции выходов S и P для этого случая определяется как
S=(A+B)+Pi-1; (9-3) Pi+1=AiBi ^ (A+B) Pi-1 (9-4)
Операции сложения подчиняется переносительному закону, из которого следует, что входы сумматора можно менять местами без ущерба для результата.
Исходя из таблицы истинности сумматора, можно написать следующие булевые уравнения для сигналов суммы и переноса
_ _ _ __ _ __
Si=AiBiPi-1 ^ AiBiPi-1 ^ AiBiPi-1 ^ AiBiPi-1
_ _ __
Pi=AiBiPi-1 ^ AiBiPi-1 ^ AiBiPi-1 ^ AiBiPi-1
В уравнениях представлены только те члены, для которых Si=1 и Pi=1, т.е. первый член функции Si относится к первой строке таблицы истинности, второй член ко второй и т.д. Сходным образом для функции P первый член принадлежит третей строке, второй- пятой и так до седьмой. Уравнения поддаются оптимизации, в результате которой получается