Файл: Тема. 14. Экспертные методы качественного анализа риска.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 51
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2. Дать экспресс-оценку и классификацию идей. Присутствуя на творческих совещаниях специалистов, ведущий может мысленно проводить классификацию полученных идей, относить их к различным направлениям. Параллельно целесообразно оценивать психологический фон дискуссии.
3. Методы качественного анализа на основе экспертного ранжирования и оценок сравнительной предпочтительности.
Метод парных сравнений. Один из наиболее распространенных методов оценки сравнительной предпочтительности альтернативных вариантов. Согласно данному методу эксперту предлагается сравнить объекты (риски, причины, источники) попарно, используя шкалу отношений. При сравнении пары объектов возможно либо отношение строгого порядка, либо отношение эквивалентности. Т.е. эксперт использует понятия больше, меньше, равно; лучше, хуже, неразличимо. Степень предпочтения параметров заранее считается не известной, она определяется в результате обработки полученных оценок. Результаты оценивания фиксируются в виде квадратной матрицы смежности парных сравнений в виде знаков:
>, если хi>хj ,
<, если хi<хj ,
=. если хi = хj ,
Допустим, эксперту предлагается сравнить значимость шести причин потери рынка: 1)высокая цена, 2) низкое качество, 3)неэффективная реклама, 4) появление новых конкурентов, 5)отсутствие обслуживания, 6)отсутствие электронной торговли. Результаты оценивания, представленные в виде матрицы парных сравнений приведены в таблице. Обозначим i - номер строки, j - номер столбца.
Таблица 23.Матрица парных сравнений (в шкале отношений)
| | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 |
| Х1 | = | > | > | < | > | > |
| Х2 | < | = | > | < | = | < |
| Х3 | < | < | = | = | < | > |
| Х4 | > | > | = | = | > | > |
| Х5 | < | = | > | < | = | = |
| Х6 | < | > | < | < | = | = |
Далее строится квадратная матрица А= | aij |
г
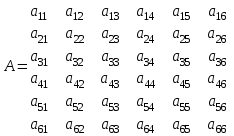
де aij= 1+у, если хi>хj ,
aij= 1- у, если хi<хj ,
aij= 1, если хi = хj , где у любое рациональное число в заданном интервале.
Примем у = 1, тогда матрица парных сравнений получит следующий вид:
Таблица 24.Матрица парных сравнений
| | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 |
| Х1 | 1 | 2 | 2 | 0 | 2 | 2 |
| Х2 | 0 | 1 | 2 | 0 | 1 | 0 |
| Х3 | 0 | 0 | 1 | 1 | 0 | 2 |
| Х4 | 2 | 2 | 1 | 1 | 2 | 2 |
| Х5 | 0 | 1 | 2 | 0 | 1 | 1 |
| Х6 | 0 | 2 | 0 | 0 | 1 | 1 |
Далее в расчет вводится понятие "итерированная сила" порядка "К" параметров в виде матрицы-столбца Р(К), которая определяется в общем случае, как
Р(К)=А*Р(К-1) (58)
где К=1,2,…m
И
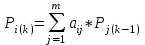
терированная сила объекта хiопределяется как произведение строки матрицы А на столбец матрицы Р(К) по формуле (59)
В начале расчета принимается итерированная сила Р(К)=1, т.е. для определения Р1(К) берется Р1(0)=1:
И
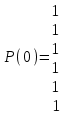
сходную матрицу А умножаем на Р(0).
Д
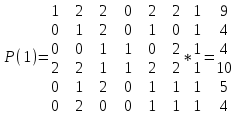

алее этот процесс продолжается с учетом полученной итерированной силы предыдущей итерации
Практическую ценность в данном методе представляет так называемая нормированная итерированная сила k-того порядка i-того параметра Р
iотн(k) именно она трактуется как значение коэффициента весомости i-того параметра (60), (61).
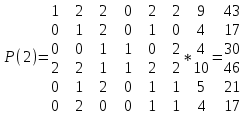
П
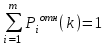
роизведем вычисление нормированной итерированной силы второго порядка.
Р
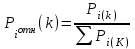
1отн(2)= 43/174 =0,2471
Р2отн(2)=17/174=0,0977
Р3отн(2) =30/174=0,1724
Р4отн(2) =46/174=0,2644
Р5отн(2) =21/174=0,1207
Р6отн(2) =17/174=0,0977
С каждой последующей итерацией результаты расчетов уточняются. Ограничившись в нашем примере двумя итерациями, можно сделать вывод, что эксперт следующим образом оценил весомость параметров причин потери рынка: 1)высокая цена – 26%, 2) низкое качество – 25%, 3)неэффективная реклама -17%, 4) появление новых конкурентов – 12%, 5)отсутствие обслуживания – 12%, 6)отсутствие электронной торговли – 10%.
При использовании метода парных сравнений нередко приходится сталкиваться с непоследовательностью и даже противоречивостью оценок эксперта. В этих случаях необходимо проведение специального анализа результатов экспертизы. Отметим также, что при достаточно большом числе оцениваемых альтернативных вариантов процедура парного сравнения всех возможных их пар становится трудоемкой для эксперта. В этом случае целесообразно применение соответствующих модификаций метода парных сравнений. Например, если предположить непротиворечивость оценок эксперта, то практически достаточно однократного предъявления каждого альтернативного варианта в паре с каким-либо другим. Если сравнение пар объектов производится отдельно по различным показателям или сравнение осуществляет группа экспертов, то по каждому показателю или эксперту составляется своя таблица результатов парных сравнений.
3.4.Метод множественных сравнений.Отличается от парных сравнений тем, что экспертам последовательно предъявляются не пары, а тройки, четверки, ..., m-ки (m
Метод векторов предпочтений. Согласно этому методу эксперту предъявляется вся совокупность оцениваемых альтернативных объектов и предлагается для каждого объекта указать, сколько, по его мнению, других альтернатив лучше (предпочтительнее) данного объекта. Полученная информация представляется в виде вектора. Первая компонента вектора - число альтернативных объектов, которые предпочтительнее первого объекта, вторая компонента -
число альтернативных объектов, которые предпочтительнее второго объекта, и т. д. Например, если оценивается 10 альтернативных объектов, то вектор предпочтений может выглядеть так: (3, 7, 0, 4, 8, 6, 1, 9, 5, 2). Если в векторе предпочтений каждое число встречается только один раз, то экспертом указано строгое ранжирование альтернативных объектов по предпочтительности. В противном случае полученный результат не является строгим ранжированием, что отражает затруднения эксперта при оценке сравнительной предпочтительности отдельных альтернативных объектов. Метод векторов предпочтений отличается сравнительно малой трудоемкостью. При коллективной экспертизе, проводимой с использованием метода векторов предпочтений, целесообразно рассчитать результирующее коллективное ранжирование, отражающее коллективную точку зрения всех экспертов.
Метод средней точки. Метод используется, когда оцениваемых объектов достаточно много. Эксперт должен выбрать самый лучший и самый худший из совокупности альтернативных объектов. Иногда эксперту предлагается дать им количественную или условно количественную оценку. Далее эксперту предлагается выбрать третий объект, оценка которого расположена посредине между значениями наилучшим и наихудшим объектом и равна середине соответствующего отрезка (1/2 суммы оценок наилучшего и наихудшего объектов). Далее эксперт указывает альтернативные объекты, находящиеся в середине каждого из полученных отрезков. Завершением процедуры считается этап, на котором определена сравнительная предпочтительность всех предложенных экспертам альтернативных объектов.
Метод последовательных сравнений (метод конфигураций, метод Черчмена – Акофа). Метод используется для количественной оценки сравнительной предпочтительности альтернативных объектов. Эксперт определяет коэффициенты весомости (важности), которые отражают степень предпочтительности оцениваемого альтернативного объекта (варианта, параметра, свойства), его вклад в достижение конечного результата. Коэффициенты весомости должны отвечать требованиям неотрицательности, неравенства нулю и требованию равенства суммы коэффициентов единице или ста. Коэффициент весомости отражает вклад объекта в достижение конечного результата. Метод последовательных сравнений целесообразно использовать при сравнении объектов, не