Достоинством ранжирования как метода экспертных оценок является простота осуществления процедур, не требующая обучения экспертов, недостатком - практическая невозможность упорядочения большого числа объектов. При включении в оцениваемую совокупность более 10-15 объектов эксперты затрудняются в их ранжировании. Это объясняется необходимостью рассматривать одновременно все объекты как единую совокупность. При увеличении количества объектов количество связей между ними растет пропорционально квадрату количества объектов. Психологические возможности человека ограничивают размер оцениваемой совокупности взаимосвязей между объектами. Поэтому при ранжировании большого числа объектов эксперты могут допускать существенные ошибки.Для сравнения большого количества альтернатив рекомендуется применять различные модификации метода. Например, можно применить двухэтапную процедуру, на первом этапе альтернативы разбиваются на упорядоченные по предпочтению классы с помощью метода экспертной классификации, а на втором происходит их ранжирование в рамках соответствующего класса.

Методы оценки согласованности мнений экспертов

Предпосылкой, гарантирующей качество экспертного прогноза, является высокая согласованность мнений экспертов. Ее оценка при обработке и анализе результатов экспертного ранжирования может включать в себя решение сле­дующих задач:

• 
  определения тесноты связи между ранжированными рядами оценок двух экспертов;
  
• 
  определения тесноты связи между произвольным числом ранжированных объектов;
  
• 
  оценки согласованности мнений экспертов в группе, содержащей
  более двух экспертов.
  

В первых двух случаях используются коэффициенты ранговой кор­реляции Спирмена или Кендалла, а в третьем случае - коэффициент конкордацииКендалла.

Коэффициенты ранговой корреляции Спирмена и Кендалла

Коэффициент ранговой корреляции Спирменаможет использо­ваться как при строгом, так и при нестрогом ранжировании. Последовательность расчета коэффициента Спирмена для группы экспертов из двух человек.

1. 
   Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию или убыванию.
   
2. 
   Определить разности рангов каждой пары сопоставляемых значений (d).
   
3. 
   Возвести в квадрат каждую разность и суммировать полученные результаты.
   
4. 
   Вычислить коэффициент корреляции рангов по формуле:
   

---

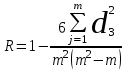(62)

5. 
   Определить статистическую значимость коэффициента при помощи t-критерия, рассчитанного по следующей формуле:
   

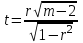(63)
Статистическая значимость полученного коэффициента оценивается при помощи t-критерия Стьюдента. Если рассчитанное значение t-критерия меньше табличного при заданном числе степеней свободы, статистическая значимость наблюдаемой взаимосвязи - отсутствует. Если больше, то корреляционная связь считается статистически значимой. При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента равные 0,3 и менее - показателями слабой тесноты связи; значения более 0,4, но менее 0,7 - показателями умеренной тесноты связи, а значения 0,7 и более - показателями высокой тесноты связи.

Для оценки степени близости мнений двух экспертов при строгом ран­жировании можно также применять коэффициент корреляции КендаллаС этой целью в обоих ранжированных рядах рассматривают все возмож­ные пары каких-либо элементов и выясняют, согласованы они или нет.

Для оценки согласованности мнений в группе, включающей более двух экспертов, чаще всего используют коэффициент конкордацииКендалла.

Коэффициент конкордацииКендалла (W) показывает степень согласованности мнений экспертов по важности каждого из оцениваемых направлений.

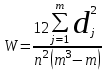
( 63 ) , где
n количество экспертов,

m количество объектов,

d_j отклонение суммы рангов по j-тому объекту от среднего значения рангов.

Если среди рангов, данных одним экспертом, есть равные, формула ( 63) приобретает следующий вид:
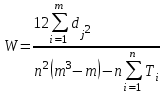(64)
если W = 1 полная согласованность мнений экспертов,

W = 0 полная несогласованность мнений экспертов.

Традиционно коэффициент конкордации Кендалла менее 0,75 свидетельствует о недостаточной согласованности мнений экспертной группы, чтобы по результатам опроса экспертов можно было построить достоверный прогноз.

---

Метод ранговой корреляции

Последовательность расчетов методом ранговой корреляции:

1. Получение индивидуальных экспертных оценок относительно важности, значимости, приоритетности оцениваемых параметров или направлений. Оценки экспертов даются в виде весовых коэффициентов, которые могут принимать значение от 0 до 1, сумма коэффициентов, данных одним экспертом должна равняться единице.

2. Ранжирование оценок важности, данных экспертами. Каждая оценка, данная i-тым экспертом, выражается рангом (Rij)  числом натурального ряда, таким образом, что значение 1 дается максимальной оценке, а n минимальной. Если среди оценок, данных i-тым экспертом, есть одинаковые, то этим оценкам присваивается одинаковый ранг, равный среднему арифметическому соответствующих чисел натурального ряда. Например, если максимальное количество баллов получили одновременно два направления, то их ранг можно рассчитать как (1+2)/2, и следующий объект получит ранг равный 3. Если же максимальное количество баллов получили одновременно три направления, то каждое из них получит ранг равный (1+2+3)/3=2, а следующий по значимости объект получит ранг равный 4.

3. Расчет суммы рангов по каждому направлению (Sj)

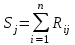(65)
4. Расчет среднего значения суммы рангов по всем направлениям (S).
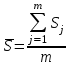(66), где
m количество оцениваемых направлений

j номер направления

5. Расчет отклонения суммы рангов по j-тому направлению от среднего значения суммы рангов (dj).

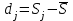(67)
6. Расчет показателя 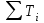, характеризующего равные ранги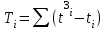
(68), где
t_i количество равных рангов в i-той группе.

7. Расчет коэффициента конкордации, выводы о согласованности мнений экспертов.

8. Анализ значимости исследуемых параметров. Параметр с наименьшей суммой рангов имеет наибольшее значение. Средний коэффициент весомости определяется как отношение величины обратной сумме рангов к их сумме.

---

---

Смотрите также файлы

• Что делала собака Охраняла животных, выслеживала и гнала зверя во время охоты.docx

• Занятие 3 Практическое задание Задание.docx

• Юсп 214 Практика это часть образовательного процесса.docx

• Центр образования естественнонаучной и технологической направленностей в общеобразовательной организации.pdf

• Отчет по Цифровой грамотности студент гр з353090210001 Рахматов К. Ф. Проверил.docx