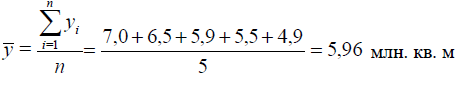Относительные показатели: динамики, плана, координацииИсходные данные за 2002 год:

Численность населения	145,2 млн. чел.
Численность городского населения	106,4 млн. чел.
Численность сельского населения	38,8 млн. чел.
Численность мужчин	77,6 млн. чел.
Численность женщин	67,6 млн. чел.
Площадь России	17,075 млн. км2

1. Рассчитаем относительный показатель динамикиОПД показывает во сколько раз текущий показатель превышает базисный или какую долю от базисногосоставляет.Примем за базу сравнения численность населения в 1990 году равную 147,7 млн. ч.Убыль населения за 12 лет составила 1,7% (100-98,3)2. Рассчитаем относительный показатель плана и реализации планаПримем значение планируемого показателя в 2003 году равным 146 млн. 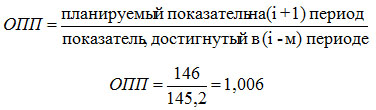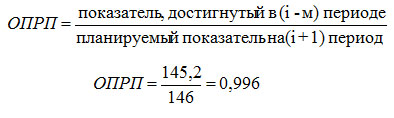чел.Численность населения по плану превысит достигнутую в 2002 году на 0,6%Численность населения достигнутая в 2002 году меньше планируемой на 0,4%3. Рассчитаем относительный показатель структурыОПС показывает, какой удельный вес имеет та или иная часть совокупности в общем итоге.Для городского населения ОПС = 106,4:145,2 = 0,733Доля городского населения в общей численности составляет 73,3%Для сельского населения ОПС = 38,8:145,2 = 0,267Доля сельского населения в общей численности составляет 26,7%4. 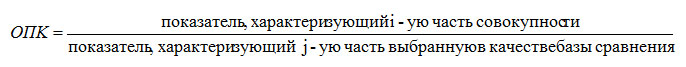Рассчитаем относительный показатель координацииОПК характеризует соотношение отдельных частей целого между собой. При

---

этом в качестве базы

сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с

экономической, социальной или другой точки зрения.

ОПК = 106,4:38,8 = 2,74

Городское население превышает сельское в 2,74 раза
5. Рассчитаем относительный показатель интенсивности



В знаменателе укажем площадь РФ (17,075 млн. км²) и ОПИ можно будет назвать показателем плотности населения

ОПИ = 145,2:17,075 = 8,5 чел./кв. м.
6. Рассчитаем относительный показатель сравнения



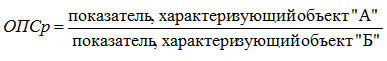
ОПСр представляет соотношение одноименных абсолютных показателей, характеризующих разные объекты

Рассчитаем во сколько раз численность женщин превосходила численность мужчин в 2002 г.

ОПСр = 77,6:67,6 = 1,148

Или численность женщин превосходит численность мужчин на 14,8%.
Анализ ряда динамики

Добыча нефти характеризуется следующими данными: 

Годы	Добыча нефти, тыс. т
1-ый	150
2-ой	210
3-ий	248
4-ый	286
5-ый	320
6-ой	337

1. Абсолютный прирост цепной (Δy_ц) – это разность между текущим уровнем ряда и предыдущим:Δy_ц =y_i – y_i-1Так, во 2-ом г. прирост добычи нефти в сравнении с первым годом составит:Δy_{ц2-й год} = y₂ – y₁ = 210 – 150 = 60 тыс. т.В 3-ем году прирост добычи нефти в сравнении со 2-м годом составит:Δy_{ц 3-й год} = 248 – 210 = 38 тыс. т.Аналогично исчисляются абсолютные приросты за последующие годы. Результаты расчётов занесём в таблицу.2. Абсолютный прирост базисный (Δy_б) – это разность между текущим уровнем ряда и уровнем ряда, выбранным за базу сравнения:Δy_б = y_i – y₀Так как в задании не указано

---

, какой год взять в качестве базисного года, по умолчанию будем считать базисным 1-й год. 

Абсолютный прирост базисный во 2-ом г. совпадает с цепным абсолютным приростом в этом году:

Δy_б = 210 – 150 = 60 тыс. т

в 3-ем году базисный абсолютный прирост равен:

Δy_б = y₃ – y₂ = 248 – 150 = 98 тыс. т 

и т.д (гр. 3 расчётной таблицы).

3. Темп роста (Тр) – отношение уровней ряда динамики, которое выражается в коэффициентах и процентах.

Цепной темп роста исчисляют отношением текущего уровня к предыдущему:



(гр. 5 расчётной таблицы);      

базисный – отношением каждого последующего уровня к одному и тому же уровню, принятому за базу сравнения:



(гр. 4 расчётной таблицы).

4. Темп прироста (Тпр) так же может быть цепной или базисный.

Цепной рассчитывается как отношение абсолютного прироста к предыдущему уровню ряда динамики:



5. Базисный темп прироста рассчитывается как отношение абсолютного прироста к базисному уровню ряда динамики:



Если предварительно был вычислен темп роста, то темп прироста можно рассчитать как разность между темпами роста и единицей, если темпы роста выражены в коэффициентах:

Тпр= Тр – 1;

или как разность между темпами роста и 100%, если темпы роста выражены в процентах:

Тпр= Тр – 100%

(гр. 6 и 7 расчётной таблицы).

Расчётная таблица

Годы	Добыча нефти, тыс. т	Абсолютный прирост базисный, тыс. т	Абсолютный прирост цепной, тыс. т	Темп роста базисный, %	Темп роста цепной, %	Темп прироста базисный, %	Темп прироста цепной, %
А	1	2	3	4	5	6	7
1-ый	150	0	-	100,00	-	-	-
2-ой	210	60	60	140,00	140,0	40,00	40,0
3-ий	248	98	38	165,33	118,1	65,33	18,1
4-ый	286	136	38	190,67	115,3	90,67	15,3
5-ый	320	170	34	213,33	111,9	113,33	11,9
6-ой	337	187	17	224,67	105,3	124,67	5,3

---

Из таблицы видно, что добыча нефти росла от года к году. Однако прирост добычи с каждым годом становился меньше.6. Средний уровень ряда определяется в данном случае по формуле средней арифметической простой, где в числителе сумма уровней динамического ряда, а в знаменателе их число:7. Среднегодовой темп роста ряда динамики рассчитывается по формуле средней геометрическойПТр – произведение цепных темпов роста (в коэффициентах),  – конечный базисный темп роста (в коэффициентах),n – число темпов.8. Среднегодовой темп прироста ряда динамики:Добыча нефти ежегодно возрастала в среднем на 17,6%.9. Между цепными и базисными темпами роста имеется взаимосвязь:произведение цепных темпов роста (в коэффициентах) равно конечному базисному темпу роста.10. Сумма цепных абсолютных приростов равна конечному базисному абсолютному приросту:Выводы: С 1 по 6 годы добыча нефти росла от года к году. Объём добычи нефти за эти годы вырос на 124,7%, что в абсолютном выражении составило 187 т. Однако ежегодный прирост добычи с каждым годом снижался. В среднем добыча нефти ежегодно возрастала  на 17,6%.Расчет средних величин:Дан ряд чисел: 15; 15; 12; 14; 13. Найдите размах, среднее арифметическое, медиану и моду этого ряда.Решение1) Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел. В данном случае размах равен R = 15-12 = 32) Среднее арифметическое данного ряда находим по формуле средней арифметической простой. Хср = (15+15+12+14+13)/5=13,83) Для определения медианы необходимо предложенный ряд упорядочить – расположить числа, например, в порядке возрастания: 12; 13; 14; 15; 15.

---

Медиана нечетного количества чисел в дискретном ряде – это число, записанное посередине. Медиана четного количества чисел – это среднее арифметическое двух чисел, находящихся посередине.Поскольку в нашем случае количество чисел ряда нечетное, то Ме = 14.4) Мода дискретного ряда чисел – это число, которое встречается в данном ряде чаще других. 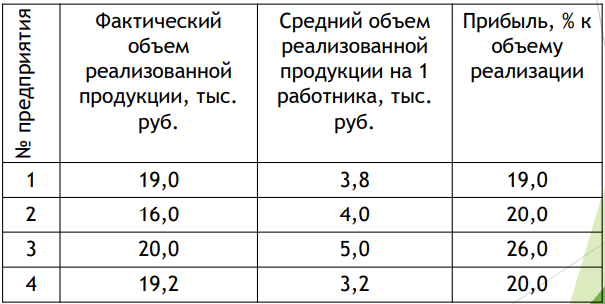Так как число 15 встречается в нашем ряде чаще других, то Мо = 15.Расчет средней величины для фактического объема реализации продукцииФормула средней арифметической простой:= (19 + 16 + 20 + 19,2) /4=74,24= 18,55 тыс. 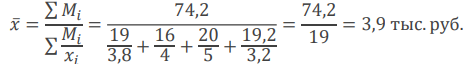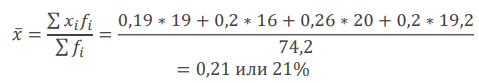рубРасчет средней величины для среднего объема реализации на 1 работника:Формула средняягармоническая взвешенная:Расчет средней величины для прибыли, % к объему реализации:Формула средней арифметической взвешеннойРасчёт среднего уровня ряда динамики где уi – уровень ряда динамики; n – число уровней; ti – длительность интервала времени между уровнями. Определим средний уровень ряда динамики, представленного в таблице:

Ввод в действие жилых домов (млн. кв. м.) Год, t	2001	2002	2003	2004	2005
Общая площадь, млн. кв. м	7,0	6,5	5,9	5,5	4,9

В данном случае имеет место интервальный ряд с равноотстоящими уровнями. Для расчётов используем формулу средней арифметической:

---

Смотрите также файлы

• Сауалнама дісі келесі формаларда олданылады Метод опроса применяется в таких формах, как.docx

• Выбор и расчет силового тиристорного преобразователя.docx

• Гигиена детей подростков.odt

• Правотворческий процесс.docx

• Сравнительный анализ примерных рабочих программ начального общего образования и действующих программ по предмету Сравнительный анализ примерной рабочей программы начального общего образования Русский язык.docx