Решение этого уравнения для нормальной помехи дает следующее выражение

для оптимального порогового напряжения:

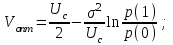
28 билет

1. 
   Некогерентный прием сигнала ДАМ.
   

Сущность оптимального приёма состоит в том, что в приёмнике необходимо применить такую обработку смеси сигнала и помехи, чтобы обеспечить выполнение заданного критерия. Данная совокупность правил обработки в приёмнике носит название алгоритма оптимального приёма заданного сигнала на фоне помех. Алгоритм находят статическими методами, зная параметры передаваемых сигналов и вероятностные характеристики помех. когерентный приёмник знает, где начало и конец у 1 или 0, а некогерентный – нет

Оптимальный приемник дает максимальную помехоустойчивость, но его схема довольно сложна в реализации. В частности, необходимо знать образцы принимаемых сигналов с точностью до фазы. Если начальная фаза сигнала неизвестна, то используются неоптимальные, некогерентные способы приема.

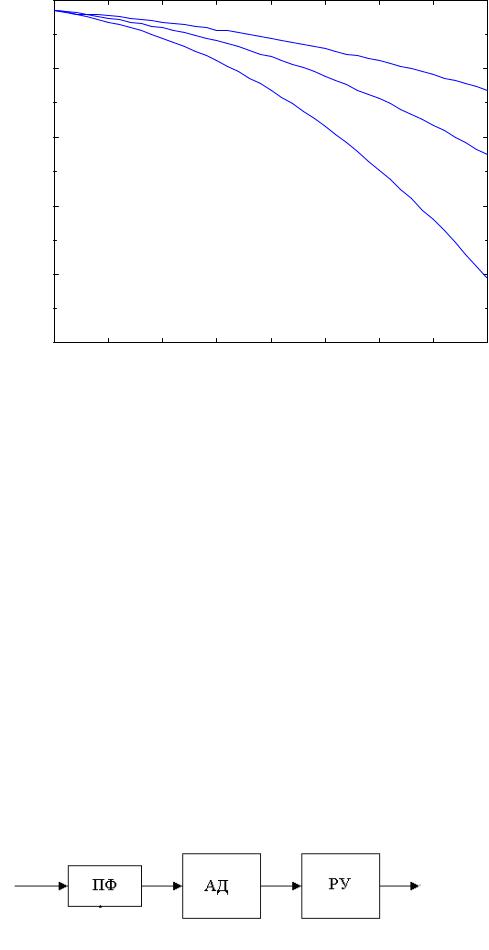
Структурная схема некогерентного демодулятора сигнала ДАМ показана на рис.2.5. Обозначения на рис.2.5 следующие: ПФ-полосовой фильтр, АД – амплитудный, некогерентный детектор, РУ – решающее устройство.

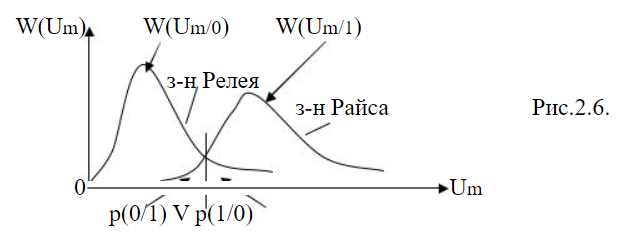
Если на входе ПФ действует сигнал в сумме с нормальным шумом, то при передаче 0 напряжение на выходе АД распределено по закону Релея W(Um/0), а при передаче 1 - по закону Райса W(Um/1) (рис. 2.6).



При оптимальном пороговом напряжении V площади под соответствующими ФПВ характеризуют вероятности ошибок р(1/0) и р(0/1). Вероятность ошибки для некогерентного приема сигнала ДАМ определяется по формуле:

	р = 0.5 ехр (-h2/4 )	(2.18)
где h2 - отношение с/ш на выходе ПФ.

---

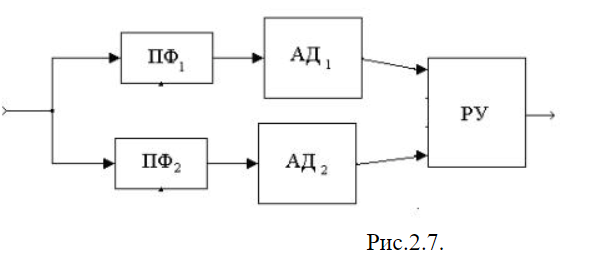
Структурная схема некогерентного демодулятора сигнала ДЧМ показана на рис.2.7. Т.к. при передаче сигнала ДЧМ передаются две разные частоты, то на приеме необходимо иметь два ПФ и два АД. РУ принимает решение, соответствующее большему напряжению. ФПВ на выходе АД1 и АД2 аналогичны рассмотренным выше. Например, при передаче 1 на выходе АД1 имеем распределение Райса, а на выходе АД2 распределение Релея. Вероятность ошибки для некогерентного приема сигнала ДЧМ определяется по формуле:

р = 0.5 ехр (-h2/2 )

(2.19)

2.Дискретизация аналоговых сигналов.

Основным требованием при дискретизации сигнала является наличие принципиальной возможности восстановления аналогового сигнала. Операция дискретизации, которая иногда называется стробированием, интерпретируется как операция перемножения входного сигнала последовательность прямоугольных импульсов (стробов)   с частотой повторения   , рис.2.



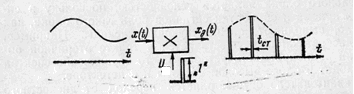
Рис.2

Форма импульсов в общем случае может быть произвольной, их амплитуда принимается равной логической единице. Длительность импульсов много меньше времени корреляции аналогового процесса , поэтому импульсы дискретизированного сигнала   повторяют форму стробов, а их амплитуды равны выборкам входного аналогового сигнала.Спектр дискретизированного сигнала практически совпадает по форме со спектром амплитудно-модулированного колебания. Для случая прямоугольных импульсов выборки вид спектра показан на рис.3. Этот спектр содержит спектр исходного аналогового сигнала,   (на рис.3 заштрихован) и его копии, повторяющиеся с периодичностью частоты дискретизации .

---

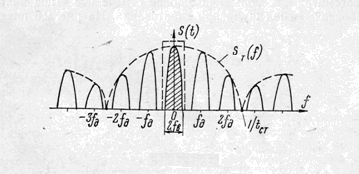
Рис.3.

Огибающая спектра   определяется видом спектра прямоугольного импульса . График на рис.3 соответствует случаю, когда   . Восстановление исходного аналогового сигнала возможно с помощью идеального фильтра нижних частот, АЧХ которого на рис. 3 показана штриховым прямоугольником. Если   , то восстановление исходного аналогового сигнала оказывается невозможным. При это возникают ошибки двух родов: ошибки усечения и ошибки наложения. На рис 4.проиллюстрировано происхождение этих ошибок. Штриховой линией показан спектр исходного аналогового сигнала, сплошной кривой – спектр отфильтрованного сигнала.



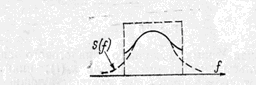
Рис.4

Срез в спектре восстановленного сигнала обусловлен фильтрацией, а подъем в области верхних частот – эффектом наложения с ближайшей копией спектра исходного сигнала.

Обеспечение требуемого качества восстановления сигнала реальными фильтрами выполняется выбором частоты дискретизации:



Билет 29.

1) Некогерентный прием сигнала ДОФМ.

Оптимальный приемник дает максимальную помехоустойчивость, но его схема довольно сложна в реализации. В частности, необходимо знать образцы принимаемых сигналов с точностью до фазы. Если начальная фаза сигнала неизвестна, то используются неоптимальные, некогерентные способы приема.

Если фаза передаточной функции канала связи медленно флуктуирует, оставаясь практически неизменной на интервале длительности, по крайней мере двух соседних символов, посылок, то оптимальным способом передачи является ОТНОСИТЕЛЬНАЯ ФАЗОВАЯ МОДУЛЯЦИЯ (ОФМ).

При ОФМ фаза данного символа s_i отсчитывается от фазы предыдущего символа s_i-1.

При передаче 0 - фаза данного символа равна фазе предыдущего символа, при передаче 1 – фаза данного символа изменяется на π по сравнению с фазой предыдущего символа.

---

 Определим потенциальную помехоустойчивость приема двоичной ОФМ (ДОФМ).

Прием «сравнением полярностей»

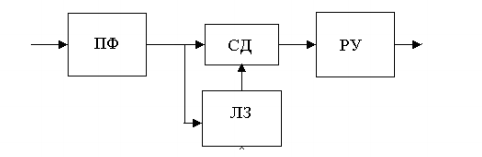
Схема демодулятора содержит фильтр ПФ, синхронный детектор СД, генератор опорного напряжения (ГОН), перемножитель (Прм), линию задержки (ЛЗ) на время Т, решающее устройство (РУ).



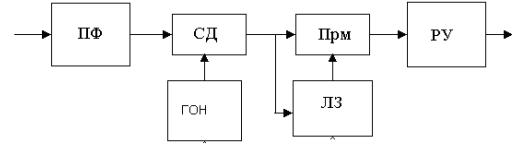
В соответствии со схемой демодулятора, ошибка при приеме сигнала ДОФМ не произойдет, если n-я и (n-1)-я посылки приняты верно, либо если n-я и (n-1)-я посылки приняты неверно. Вероятность первого события равна р₁= (1- р_ДФМ) ² , где р_ДФМ – вероятность ошибки при приеме сигнала ДФМ.

Вероятность второго события равна: р₂ = р_ДФМ ² . Полная вероятность правильного приема равна р₃ = (1- р_ДФМ) ² + р_ДФМ ² . Вероятность ошибки равна:

р = 1- (1- р_ДФМ) ² - р_ДФМ ² = 2 р_ДФМ (1- р_ДФМ) =2F (h₀√ 2 )[1-F (h₀√ 2 )];

Прием «сравнением фаз»

В соответствии со схемой демодулятора, знак напряжения на выходе демодулятора определяется знаком интеграла от произведения двух соседних по времени отрезков процесса z (t) на входе демодулятора.



Вероятность ошибки для приема «сравнением фаз» определяется по формуле: р = 0.5 ехр (-h² )

Таким ообразом и для некогерентных способов приема ДОФМ является наиболее помехоустойчивым способом передачи информации и выигрывает 2 раза по мощности передатчика по сравнению с ДЧМ, и 4 раза по сравнению с ДАМ.

2) АИМ . Параметры и характеристики.

В результате процесса дискретизации мы получим не последовательность дельта-импульсов, амплитуда которых соответствует значению непрерывного сигнала в тактовые моменты времени, а последовательность реальных, например, прямоугольных импульсов, амплитуда которых соответствует значениям непрерывного сигнала в тактовые моменты времени.

---

Рассмотрим временные диаграммы:



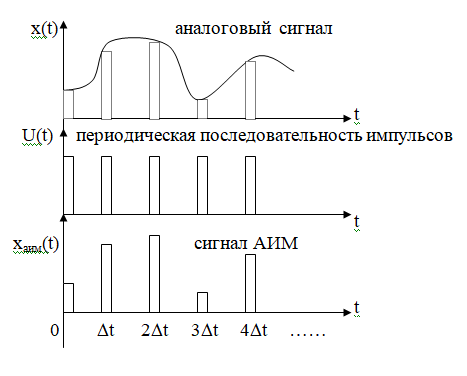
АИМ сигнал можно записать в виде:



U(t)-периодическая последовательность импульсов.

В квадратных скобках – ряд Фурье для последовательности импульсов конечной длительности.

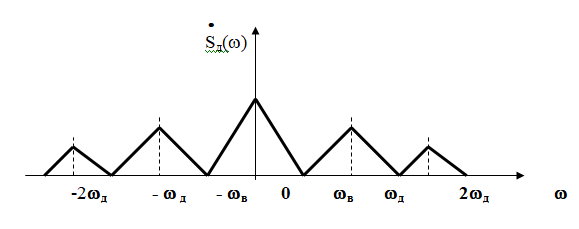
Спектр АИМ сигнала, следовательно, похож на спектр дискретизированного сигнала при дискретизации дельта - импульсами, но амплитуда составляющих спектра убывает с ростом номера гармоники: 



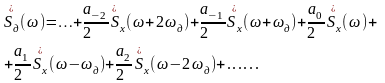
Спектр АИМ сигнала принимает вид:


Билет № 30

1. 
   Нелинейные и линейные преобразования нормального процесса
   

Нелинейное преобразование: y(t)=f[x(t)] – называется безынерционным, если y(tk) в момент времени tk зависит только от x(tk). ФПВ для процесса y на выходе:



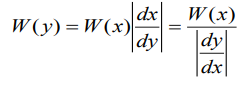
Пусть характеристика нелинейного элемента может быть аппроксимирована линейно-ломаными.




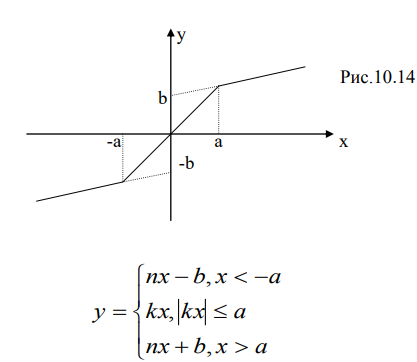
Это нелинейное устройство называется ограничителем. Пусть на входе ограничителя действует нормальный случайный процесс с нулевым средним m1x=0.



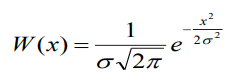
ФПВ процесса x нарисована на рис.10.15 (верхний рисунок).

Рассчитаем ФПВ процесса y:

1..Пусть: |x| <= a у=kx (k>1)



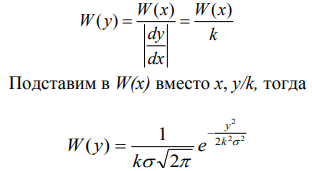
На интервале |y|  ka ФПВ для у будет нормальной, со средним значением m_1y=0, но дисперсия y, то есть _y²  k² ²  ² (т к  k 1).



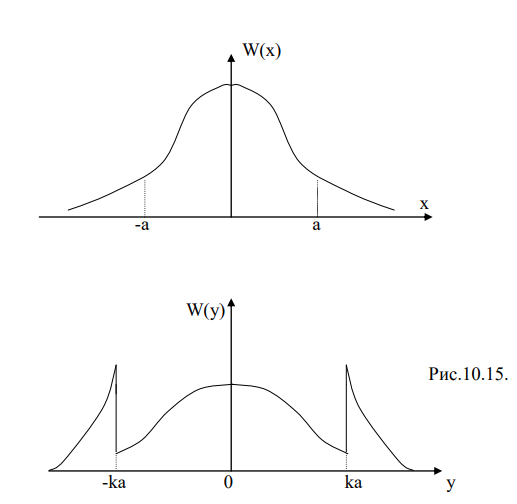
2..Пусть:

---

Смотрите также файлы

• Фамилия, имя, отчество слушателя.docx

• Бизнесплан по разведению крупно рогатого скота мясного направления 2020 год.pdf

• Таырыбы Салауаттылы денсаулы кепілі Сабаты масаты.docx

• Верхняя конечность.docx

• Работа социального педагога по организации социального опыта.doc