ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 184
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Билет 1
1.Теорема Котельникова
Теорема Котельникова: любая непрерывная функция, спектр которой не содержит частот
выше
, полностью определяется своими отсчетами, взятыми через интервал времени
С точки зрения математики теорема Котельникова означает представление сигнала в виде ряда:
Ряд Котельникова – это разложение сигнала
в ряд по ортогональным функциям:
2.ИКМ.
Чтобы получить на входе канала связи ИКМ-сигнал из аналогового, мгновенное значение аналогового сигнала измеряется аналого-цифровым преобразователем (АЦП) через равные промежутки времени. Количество оцифрованных значений в секунду (или скорость оцифровки, частота дискретизации) должно быть не ниже 2-кратной максимальной частоты в спектре аналогового сигнала (по теореме Котельникова) (Теорема Котельникова: любая непрерывная функция, спектр которой не содержит частот
выше
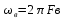, полностью определяется своими отсчетами, взятыми через интервал времени
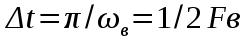). Мгновенное измеренное значение аналогового сигнала округляется до ближайшего уровня из множества заранее определённых значений. Этот процесс называется квантованием. Количество уровней всегда берётся кратным степени двойки, например, 23=8, 24=16, 25=32, 26=64 и т.д. Номер уровня может быть соответственно представлен 3, 4, 5, 6 и т.д. битами. Таким образом, на выходе модулятора получается набор битов (0 и 1).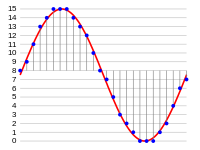
При представлении дискретного сигнала в виде чисел с ограниченной разрядностью происходит их округление. Разность между исходным и округленным значениями - шум квантования.
Билет 2
1.Дискретизация непрерывных сигналов.
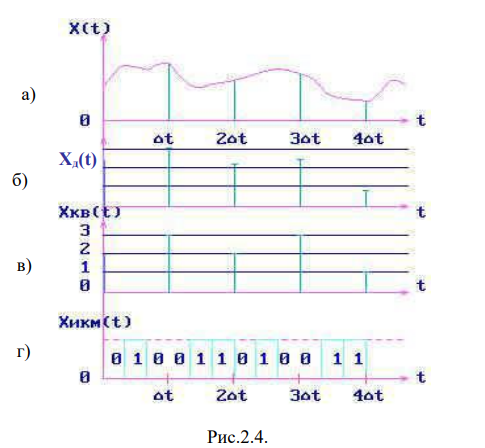
2.Оптимальный приемник.
Оптимальный приемник – это такой приемник, который обеспечивает максимальную помехоустойчивость при данном способе передачи (данном виде сигнала) и данном виде помех. Различают оптимальный приемник полностью известных сигналов и оптимальный приемник не полностью известных сигналов, когда приемник использует не все параметры сигнала, например, не учитывает фазу несущего колебания.
Билет 3
1.Восстановление непрерывных сигналов из отсчетов.
Восстановление непрерывных сигналов из отсчетов
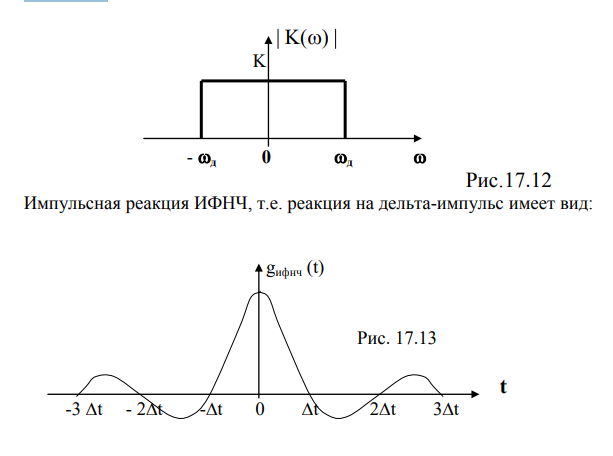
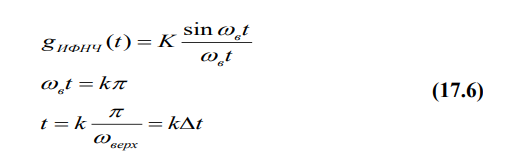
Первая формула - это выражение для импульсной реакции ИФНЧ, вторая и третья формулы определяют моменты времени, для которых g ИФНЧ(t) обращается в ноль. Cо спектральной точки зрения мы пропускаем дискретизированный сигнал, имеющий спектр в соответствии с рис.17.9 или 17.11, через ИФНЧ с АЧХ рис.17.12. Очевидно, что на выходе ИФНЧ получим спектр: S(ω)= K Sд(ω) = K Sx(ω) /∆t; или для АИМ сигнала получим: S(ω)= KSд(ω) = K a0Sx(ω) /2. Таким образом, с точностью до постоянного множителя мы получили на выходе ИФНЧ спектр исходного сигнала x(t). С временной точки зрения мы получили исходный непрерывный сигнал x(t)
| 2.Сравнительная помехоустойчивость ДАМ, ДЧМ, ДФМ. Помехоустойчивость приемника определяется вероятностью ошибки при заданном отношении сигнал/помеха. Для разных видов модуляции помехоустойчивость различна. В общем виде вероятность ошибки определяется формулой:  где E - энергия элемента сигнала, N0 - спектральная мощность помехи. При оптимальной фильтрации вводится величина: 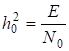 При дискретной амплитудной модуляции (ДАМ): 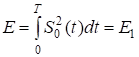 (Е равна энергии первого сигнала);. 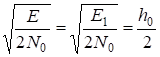 Подставив эту величину, получим: 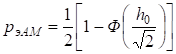 При дискретной частотной модуляции (ДЧМ): 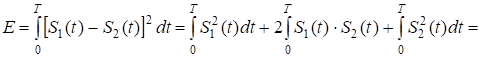 При частотной модуляции сигналы и являются взаимно-ортогональными, поэтому их функция взаимной корреляции равна нулю. Кроме того, благодаря равной амплитуде сигналов Е1 = Е2. В результате Е = 2Е1 и . 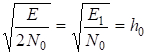 Подставив эту величину, получим:  При дискретной фазовой модуляции (ДФМ): Подставив эту величину, получим: 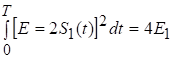 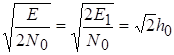  Сравнивая между собой формулы вероятностей ошибок, видно, что для достижения заданной вероятности ошибки при ДЧМ требуется величина h0 в больше, чем при ДФМ, а при ДАМ - в 2 раза больше, чем при ДФМ. Отсюда следует, что переход от ДАМ к ДЧМ дает двукратный выигрыш по мощности, а к ДФМ - четырехкратный. Причину этого можно наглядно установить, рассматривая векторные диаграммы сигналов для разных видов модуляций. Выше сказанное можно изобразить на графике: 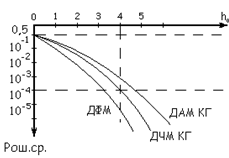 Рисунок 5 - Сравнительный график помехоустойчивости. 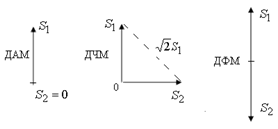 Рисунок 6 - Векторные диаграммы сигналов для разных видов модуляций.  Из рисунка 6 видно, что при ДАМ расстояние между векторами сигналов S1 и S2 равно длине вектора S1, при ДЧМ (взаимоортогональные сигналы) это расстояние равно , при ДФМ (противоположные сигналы) это расстояние равно 2S1. Энергия же пропорциональна квадрату разности сигналов. Приведенные здесь данные об энергетике сигналов ДАМ, ДЧМ и ДФМ относились в максимальным (пиковым) мощностям этих сигналов. Сигналы ДАМ имеют пассивную паузу (мощность сигнала в паузе равна нулю), поэтому по потребляемой передатчиком мощности, кроме отмеченного ранее проигрыша, имеется еще и двукратный выигрыш. С учетом этого обстоятельства, при переходе от ДЧМ к ДАМ двукратный проигрыш по пиковой мощности компенсируется двукратным выигрышем за счет пассивной паузы сигналов ДАМ, в результате чего по потребляемой мощности эти сигналы оказываются равноценными. При этом следует помнить, что при ДАМ в приемнике Котельникова трудно установить необходимый порог в сравнивающем устройстве, а в приемнике ДЧМ регулировка порога не требуется. Поэтому частотная модуляция применяется чаще, чем амплитудная. В итоге можно сделать вывод: при флуктуационной помехе типа "белого шума" из всех видов дискретной модуляции наибольшую (потенциальную) помехоустойчивость имеет фазовая двоичная модуляция с противоположными сигналами, т.е. имеющими сдвиг фаз 180о, наименьшую помехоустойчивость имеет ДАМ; ДЧМ занимает промежуточное положение. Несмотря на высокую помехоустойчивость, ДФМ имеет принципиальный недостаток - эффект "обратной работы" в когерентных модуляторах. По этой причине классическая ДФМ не получила практического применения. Для преодоления данного недостатка российским ученым Н.Т. Петровичем в 1954 г. была предложена относительная фазовая модуляция (ОФМ или DPSK), которая получила повсеместное применение в реальных системах связи.  |
Билет 4
1.Погрешности дискретизации и восстановления непрерывных сигналов
Теорема Котельникова точно справедлива только для сигналов с финитным (конечным) спектром. На рис.17.14 показаны некоторые варианты финитных спектров:
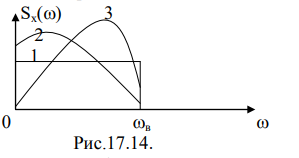
Однако спектры реальных информационных сигналов бесконечны. В этом случае теорема Котельникова справедлива с погрешностью
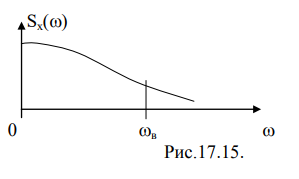
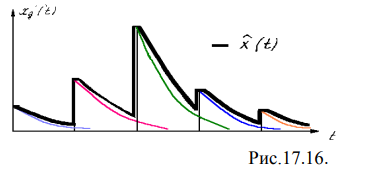
Вторая причина возникновения погрешностей - неидеальность восстанавливающего ФНЧ. Т.о. погрешность дискретизации и восстановления непрерывного сигнала определяется следующими причинами: 1) Спектры реальных сигналов не финитны. 2) АЧХ реальных ФНЧ неидеальны. Например, если в качестве ФНЧ использовать RC- фильтр, то восстановленный сигнал на его выходе будет иметь вид:
| 2.Потенциальная помехоустойчивость ДАМ, ДЧМ, ДФМ, Способность Системы связи препятствовать мешающему влиянию помех называется помехоустойчивостью. Максимально достижимая помехоустойчивость называется потенциальная помехоустойчивость, которой соответствует минимальная вероятность ошибки р (р=limNoш/N (где N –общее количество переданных символов, Nош- количество ошибок). Приемник, реализующий потенциальную помехоустойчивость, т.е. обеспечивающий минимальную вероятность ошибки, называется оптимальным приемником. (Это минимальная вероятность ошибки не может быть очень большой, но ни какой другой приемник не даст меньшей вероятности ошибки). Что бы обеспечить потенциальную помехоустойчивость оптимальный приемник должен работать по правилу: ∫[z(t)-U1(t)]2dt <∫[z(t)-U0(t)]2dt R=1; ∫[z(t)-U1(t)]2dt >∫[z(t)-U0(t)]2dt R=0 Полной характеристикой помехоустойчивости является средняя вероятность ошибки p=p(1)*p(0/1)+p(0)*p(1/0) m1=0 disp^2=G0*Ep Выводы: 1)максимальная вероятность ошибки равна: Pmax=1-F(0)=0.5 для двоичной системы связи 2)чем больше Ер, тем меньше вероятность ошибки и при Ep->inf; p=>1-F(inf)=0 3)потенциальная помехоустойчивость ОП не зависит от формы посылок, зависит только от Ер 4)наиболее помехоустойчивым будет тот вид модуляции, который обеспечивает max Ep при фиксированной мощности передатчика Epдам=Um^2 * T/2 Ердчм=Um^2 * T Ердфм=2Um^2 * T Т.о. наиболее помехоустойчивым способом передачи двоичных сигналов является ДФМ.Она выигрывает в 2 раза по мощности передатчика по сравнению с ДЧМ и в 4 раза по мощности передатчика по сравнению с ДАМ. Чем меньше мощность, тем меньше передатчик, меньше потребляемая энергия источника питания, тем он дешевле. PошДАМ=1-F(h0/2^1/2) РошДЧМ=1-F(h0) РошДФМ=1-F(h0*2^1/2) Построение кодового дерева. Энтропия – это среднее количество информации приходящееся на одно сообщение.Чем больше энтропия, тем больше информации несет один символ и тем больше скорость передачи информации Префиксные свойства: не какая короткая кодовая комбинация не может быть началом более длиной кодовой комбинации. |
Билет 5
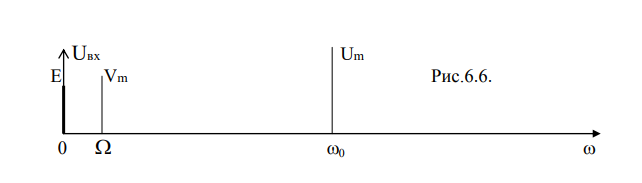
1.Амплитудный модулятор. Схема, спектры сигналов на входе и выходе.
Схема базового амплитудного модулятора имеет вид:
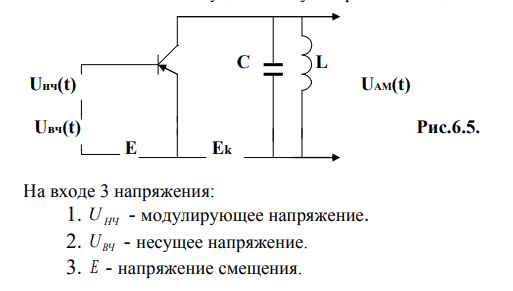
Построим спектр входного напряжения:
| 2.Помехоустойчивость оптимального приемника Анализ (2.15) позволяет сделать следующие выводы: 1. Потенциальная помехоустойчивость оптимального приемника зависит только от отношения энергии разности посылок к спектральной плотности помехи. 2. Минимальная вероятность ошибки равна 0. 3. Максимальная вероятность ошибки для двоичной системы связи равна 0.5. 4. Чем больше энергия разности посылок, тем выше помехоустойчивость системы сигналов |
Билет 6
1.Схема и СМХ амплитудного модулятора.
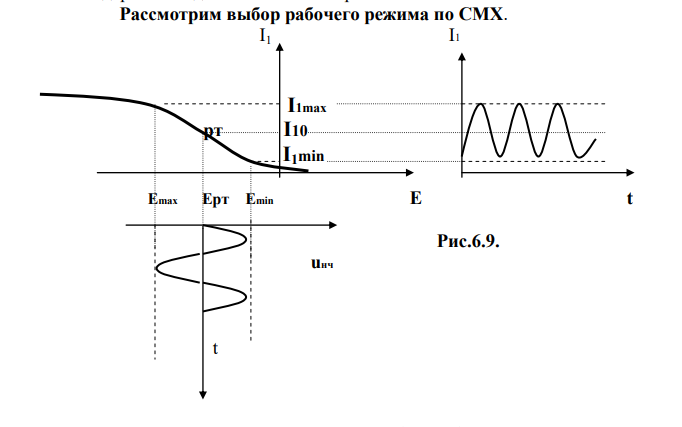
СМХ –это зависимость амплитуды 1-ой гармоники выходного тока I1 модулятора от напряжения смещения E при амплитуде вч несущей Um=const и амплитуде нч модулирующего сигнала Vm = 0.
1. Выбираем линейный участок (на глаз).
2. Определяем Еmin , Emax , Imax , Imin .
3. Выбираем рабочую точку в середине линейного участка Р.Т.(I10;ЕР. Т.)
4. Определяем максимальную амплитуду модулирующего сигнала для неискажённой модуляции:
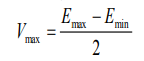
5. Определяем максимальную глубину амплитудной модуляции для неискажённых АМ:
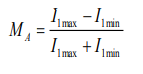
2.Энтропия. Способы ее увеличения.
Билет 7
1.СМХ частотного модулятора.
ЧМ сигнал может быть получен с помощью частотного модулятора. Частотный модулятор состоит из автогенератора и элемента с помощью которого изменяется частота автогенерации.
Автогенератор - генератор с самовозбуждением, т.е. усилитель, охваченный цепью положительной обратной связи ( колебания с выхода поступают на вход, поддерживая возникшие колебания).
2.Увеличение энтропии путем укрупнения сообщений.
Цель статистического кодирования - увеличение энтропии и, как следствие, увеличение скорости передачи информации. 23 Источник создает сообщения, символы аk , которые могут принимать значения от 1 до m. Символы статистически связаны между собой – это исходный код К1. Последовательности из n символов образуют слова, статистические связи между которыми практически отсутствуют. Осуществим укрупнение алфавита источника, будем кодировать не буквы, а целые слова Аi . Эти слова Аi являются символами нового кода К2. Вероятность символов нового кода К2 равна вероятности слов первичного кода К1 . Т.к. слово состоит из n букв , то энтропия на символ нового кода H2 больше в n раз энтропии на символ старого кода H1 . Рассмотрим пример, который подробно изложен в описании лабораторной работы №20а. Источник двоичных сообщений A и M производит слова из двух букв (AM, MA, MM, AA); буквы в слове коррелированы, слова - некоррелированы. Статистические характеристики источника следующие: p(A)=0.7 , p(M)=0.3 , p(A/A)=0.8 , p(M/A)=0.2 , p(A/M)=0.7 , p(M/M)=0.3. Т.к. между буквами существуют корреляционные связи, то энтропия источника меньше максимальной.
Билет 8
1.Амплитудный линейный детектор.
Детектор сигналов АМ предназначен для того, чтобы из ВЧ АМ сигнала получить НЧ модулирующий сигнал. Схема простейшего амплитудного диодного детектора:
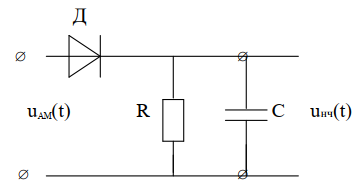
Назначение нелинейного элемента, диода – преобразование ВЧ АМ