сигнала, его нелинейное преобразование с целью создания нужных нам низких, модулирующих частот. Назначение линейной цепи, т.е. RC фильтра нижних частот (ФНЧ), выделение низкой частоты, т.е. выделение спектра модулирующего сигнала.

1. Для маленьких напряжений ВАХ диода хорошо аппроксимируется
полиномом 2-ой степени (i=aU2), поэтому детектор для маленьких
напряжений называется квадратичным. Рабочий участок ВАХ для
квадратичного детектора А-А (рис.7.2).

2. Для больших напряжений ВАХ диода аппроксимируется отрезками
прямых (линейно-ломанная аппроксимация).

Амплитудный линейный детектор

Для сильных сигналов с большой амплитудой ВАХ диода
аппроксимируется отрезками прямых:





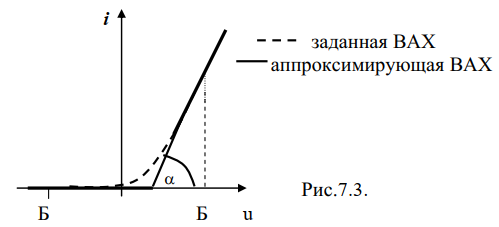
Метод анализа: метод «угла отсечки». Ток через диод имеет вид
импульсов, которые мы можем представить в виде ряда Фурье. Таким
образом, ток через диод может быть записан в виде:



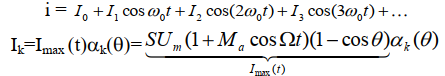
Спектр тока через диод для режима "линейный детектор"



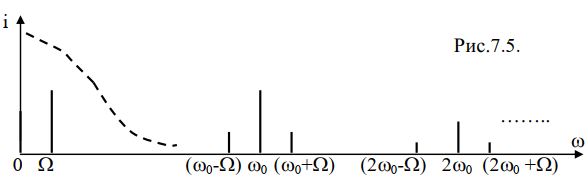
Спектр тока содержит только полезную, модулирующую частоту в низкочастотной области. При линейном детектировании отсутствуют
нелинейные искажения полезного сигнала. ФНЧ отфильтровывает
высокочастотные составляющие тока, ослабляет их в соответствии с сопротивлением RC цепи для разных частот:



Напряжения различных составляющих на выходе ФНЧ, соответственно, равны:

---

- напряжение постоянной составляющей,

- напряжение низкой, модулирующей частоты,

- напряжение несущей частоты

Спектр напряжения на выходе RC-цепочки имеет вид:

1. 
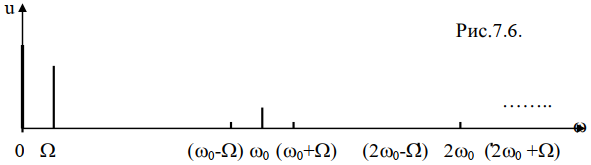
   Увеличение энтропии путем построения кодового дерева.
   

Алгоритм Хаффмена предполагает построение «кодового дерева».

а) Расположить исходные сообщения в порядке убывания (не возрастания) вероятностей;

б) Объединить два наименее вероятных сообщения в одно, вероятность которого равна сумме вероятностей объединяемых сообщений (точка объединения сообщений называется «узлом кодового дерева»);

в) Повторять шаги а) и б) до тех пор, пока не получим одно сообщение с вероятностью 1. Эта точка называется «вершиной кодового дерева». Например, кодовое дерево имеет вид рис.4.2 для источника сообщений, заданного в примере.



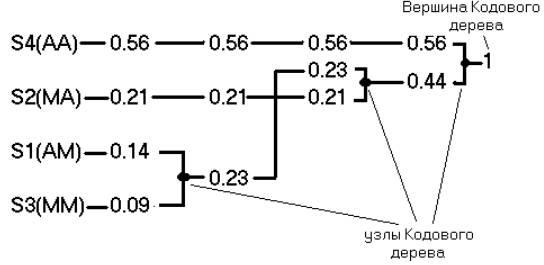
Алгоритм кодирования слов новым двоичным кодом следующий:

-идём от вершины кодового дерева к сообщению,

-если в узле мы идём вверх, то в кодовую комбинацию записывается единица, если вниз – ноль. В результате получим:
S4 => “1” ; S2 => “00” ; S1 => “011” ; S3 => “010” .

Рассчитаем энтропию нового двоичного кода. Для этого надо определить вероятности нулей и единиц в новом коде. Пусть слова исходного источника S1, S2, S3, S4 имеют вероятности и закодированы как в нашем примере. Из 100 среднестатистических сообщений будем иметь S1 - 14 сообщений; S2 – 21 сообщение; S3 - 9 сообщений; S4 - 56 сообщений. В соответствии с новым кодом имеем:

* 14 сообщений S1, т.е. 14 символов 0 и 28 символов 1;

* 21 сообщение S2, т.е. 42 символа 0;

* 9 сообщений S3, т.е. 9 символов 1 и 18 символов 0;

---

*56 сообщений S4, т.е. 56 символов 1.

символ 0: N0 = 14*1 + 21*2 + 9*2 = 74 штуки;

символ 1: N1 = 14*2 +9*1 + 56*1= 93 штуки.

Вероятность появления единиц и нулей:

p(1) = N1/(N1+N0)=93/167 = 0.557; p(0)=0.443.

Энтропия нового двоичного источника H’’:

H’’ = - p(1) log p(1) – p(0) log p(0)= - 0.557log0.557–0.443log0.443 =
=0.994 (двоичных ед./символ).
Билет 9.

1. 
   Амплитудный квадратичный детектор.
   

В этом случае ВАХ диода аппроксимируется полиномом второй степени и, следовательно, для определения спектра
тока через диод используется метод "кратных дуг". На вход детектора
подаем амплитудно-модулированный сигнал, т.е. выражение для АМ
сигнала надо подставить в полином:





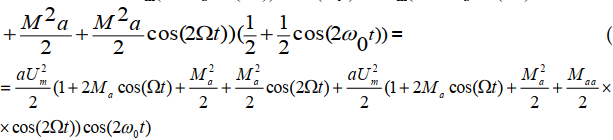
В соответствии с полученным выражением построим спектр тока через
диод:



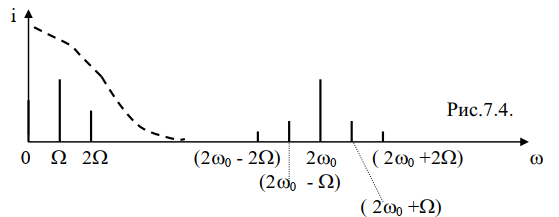
ФНЧ выделяет низкочастотные составляющие тока, т.к. его АЧХ,
показанная пунктиром на рисунке имеет вид:



Следовательно, ФНЧ выделяет:
- постоянную составляющую с частотой равной 0,

- полезную составляющую с частотой модулирующего колебания ,то
есть: I= aU²mMА

- вторую гармонику полезного сигнала с частотой

Постоянная составляющая легко отделяется разделительной емкостью, которая включается между выходом детектора и входом следующего каскада (обычно, это УНЧ) .

При квадратичном детектировании кроме полезной составляющей с частотой  возникают нелинейные искажения полезного сигнала с частотой 2. Коэффициент нелинейных искажений равен:

---

Чем глубже, т.е. лучше модуляция, тем больше нелинейные искажения.

2. 
   Увеличение энтропии путем увеличения m.
   

Цель статистического кодирования - увеличение энтропии и, как следствие, увеличение скорости передачи информации.

Источник создает сообщения, символы а_k , которые могут принимать значения от 1 до m. Символы статистически связаны между собой – это исходный код К₁. Последовательности из n символов образуют слова, статистические связи между которыми практически отсутствуют.

Осуществим укрупнение алфавита источника, будем кодировать не буквы, а целые слова Аi. Эти слова Аi являются символами нового кода К2. Вероятность символов нового кода К2 равна вероятности слов первичного кода К1 . Т.к. слово состоит из n букв , то энтропия на символ нового кода H2 больше в n раз энтропии на символ старого кода H1 .

Порядок расчета энтропии источника зависимых сообщений:

1) Определяем общее количество N независимых слов источника. В данном случае их 4, т.к. m =2 , а n =2 (слова состоят из двух букв) , N=2²=4.

2) Определяем вероятность каждого слова:

p(AM)=p(A)*p(M/A)=0.7*0.2=0.14;

p(MA)=p(M)*p(A/M)=0.3*0.7=0.21;
p(MM)=p(M)*p(M/M)=0.3*0.3=0.09;
p(AA)=p(A)*p(A/A)=0.7*0.8=0.56;

3) Т.к. слова независимы, то энтропию источника «на слово» найдем по формуле:



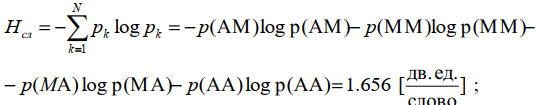
Энтропия на одну букву или символ (n=2):

Рассчитаем избыточность нашего источника, т.е. степень отличия энтропии источника от максимального значения. Так как наш источник создаёт только 2 разных сообщения A и M, т.е. является
двоичным источником, то его максимальная энтропия равна Hmax=log2 2 =
= 1 дв.ед./символ. Следовательно, его избыточность равна:



Укрупним алфавит источника и будем кодировать кодом К2 целые слова. Т.к. разных слов – 4, то нужно использовать код с основанием m=4.
АМ – первое слово S1 кодируем символом 0,

МА – второе слово S2 кодируем символом 1,

---

ММ – третье слово S3 кодируем символом 2,

АА – четвертое слово S4 кодируем символом 3.

Получили новый код К2 с основанием m=4, длиной комбинации n=1, общее число комбинаций N=mⁿ=4.

Сообщения этого кода независимы, т.к. независимы слова (между словами нет корреляции). Поэтому энтропия рассчитывается по формуле для дискретного источника независимых сообщений:



Избыточность осталась та же. Т.о., увеличив энтропию с помощью кода К2, мы не уменьшили избыточность. Это означает, что есть возможность еще более увеличить энтропию.
Билет 10

1. 
   Частотный модулятор. Схема, спектры сигналов на входе и выходе.
   

У Артёма

2. 
   Теорема Шеннона.
   

По каналу связи с полосой пропускания F , в котором действует сигнал с мощностью Рс и нормальный белый шум со спектральной плотностью энергии G₀, можно предавать информацию со скоростью сколь угодно близкой к пропускной способности канала связи:



Доказательство. Количество взаимной информации содержащейся в процессе z(t) о сигнале u(t) равно: I(Z;U)=h(Z)-h(X);

Дисперсия белого шума x(t) в полосе F: σ² = G₀F. Т.к. шум нормальный, то его дифференциальная энтропия равна: h(X)=0.5*log(2πeσ²)

Чтобы энтропия процесса z была максимальной, этот процесс должен быть нормальным случайным процессом, т.е. сигнал тоже должен быть нормальным случайным процессом с дисперсией Р_с. Тогда максимальное количество взаимной информации равно: I(Z;U)=0.5*log[2πe(Pc + σ²)] - -0.5*log(2πeσ²) = 0.5*log(1 + P_c / σ²);

Т.к процесс на выходе канала связи финитный по спектру, то он полностью определяется по теореме Котельникова своими отсчетами взятыми через интервал времени T=1/2F. Таким образом в единицу времени следует передавать 2F отсчетов. Каждый отсчёт процесса z(t) несет информацию о сигнале I(z;u). Таким образом за 1с максимальное количество, переданной по КС информации, равно: С=2F*I(Z;U)=F*log(1+Pc /G₀F)

Для того, чтобы вероятность ошибки была сколь угодно малой (рош→0), необходимо использовать бесконечно длинные кодовые комбинации, т.е время задержки принятия решения бесконечно велико. Из формулы для пропускной способности следует, что при F→ ∞ величина C стремится к пределу равному С∞=Р

---

Смотрите также файлы

• Фамилия, имя, отчество слушателя.docx

• Бизнесплан по разведению крупно рогатого скота мясного направления 2020 год.pdf

• Таырыбы Салауаттылы денсаулы кепілі Сабаты масаты.docx

• Верхняя конечность.docx

• Работа социального педагога по организации социального опыта.doc