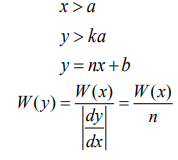
Выражаем x через у, т.е. .



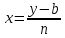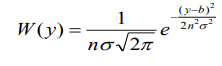
Это нормальная ФПВ со средним значением b и дисперсией 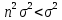, (n<1).

3..Пусть:



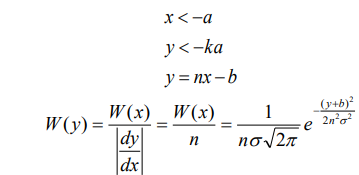
Это нормальная ФПВ,

---

m₁= -b и дисперсия n² ² .

ФПВ процесса y дана на рис.10.15 (нижний рисунок).

Линейная инерционная система – это линейный фильтр. В этом случае процесс на выходе системы у(t1) зависит от входного процесса x не только в момент времени t1, но и от значений x в предшествующие и последующие моменты времени:

1. 
   Если процесс на входе ЛЭЦ нормальный, то у тоже нормальный случайный процесс, но его числовые характеристики отличаются от числовых характеристик процесса x и вычисляются следующим образом:
   

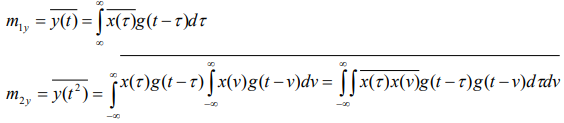
2. Если процесс на входе ЛЭЦ не нормальный, но ширина его спектра значительно больше полосы пропускания линейной цепи _x Плэц , то процесс на выходе ЛЭЦ имеет тенденцию к нормализации.

2. 
   Циклический код.
   

5.3. Циклические коды

Характерной особенностью циклических кодов является то, что циклическая перестановка символов одной комбинации, например, 1001011 дает новую комбинацию того же кода 1100101. Теория циклических кодов базируется на теории двоичных полиномов. Циклические коды – это одна из разновидностей полиномиальных кодов. Каждая комбинация записывается в виде двоичного полинома степени (n-1) с коэффициентами а_к = 0 или 1:

a(z) = аn-1z n-1 + аn-2z n-2 +…+ а1z + а0 (5.2)

Например:

1 0 1 a(z) = а2z 2 + а1z + а0 = z 2 + 1

Алгоритм формирования циклического кода на примере кода (7, 4).

Комбинации данного циклического кода состоят из 7 символов, из которых 4 символа информационные и 3 – проверочные.

1) Записываем возможные информационные комбинации из 4-х символов: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.

2) Каждую комбинацию записываем в виде полинома. Например:

---

а₁ а₂ а₃ а₄
1 0 0 1 a(z) = z 3 + 1 а3 а2 а1 а0

3. 
   Выбираем из таблиц образующий полином, степень которого соответствует количеству проверочных символов. В данном случае количество проверочных символов (n-k) =3. Выбираем полином:
   

р(z) = z 3 + z +1; 1 1 0 1

1. 
   Полином, соответствующей информационной комбинации умножается на p(z):
   

(z 3 + 1) (z 3 + z +1)= z 6 +z 4 +z +1 1010011

В результате получим 16 комбинаций циклического кода (7,4): 0000000, 0001011, 0010110 и т.д…... Код состоит из совокупности двух подмножеств по 7 комбинаций, внутри которых циклические перестановки дают остальные и двух комбинаций 0000000 и 1111111. Минимальное кодовое расстояние равно 3, т.е. данный код исправляет все одиночные ошибки.

Алгоритм декодирования циклического кода на примере кода(7,4).

1. 
   Принятая кодовая комбинация делится на образующий полином. Остаток от деления есть синдром, который указывает на позицию, где произошла ошибка. Т.к. синдром не зависит от передаваемой комбинации, а зависит только от позиции, в которой произошла ошибка, то синдромы можно вычислить заранее. Например, передавали комбинацию 0000000, под действием помехи она превратилась в 0100000, т.е. ошибка в 6-ом символе справа. Разделим 0100000 на р(z)=1101:
   

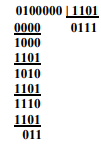
Остаток 011 и есть синдром, указывающий, что ошибка произошла в 6-ом символе справа.

2. В соответствии с синдромом формируется вектор ошибки, т.е. кодовая комбинация, которая содержит 1 в той позиции, где произошла ошибка. Для данного примера вектор ошибки V=0100000. Вектор ошибки суммируется по модулю 2 с принятой комбинацией: 0100000  0100000 = 0000000

Ошибка исправлена.
Билет № 31

1)..Среднеквадратическая погрешность дискретизации. (фильтрации)

Среднеквадратическая погрешность фильтрации

Данного вопроса нет в лекции, так что из курсовой

---

По условию курсовой, нам дана Pa - мощность (дисперсия) сообщения

Потом мы посчитали Px - мощность фильтра ФНЧ по данной формуле



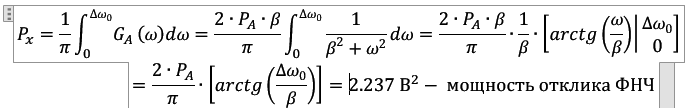
Ga - спектр плотности мощности



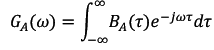
Ba - функция корреляции сообщения, которая тоже была дана по условию

Дальше мы находим среднеквадратичную погрешность фильтрации



и получается, что погрешность фильтрации это мощность сообщения минус мощность фильтра


Pa - мощность сообщения

2. 
   Оптимальный приемник
   

См. Билет № 2

Билет № 32

1).. ИКМ.

См. Билет № 1

2).. Потенциальная помехоустойчивость

См. Билет № 4

---

Смотрите также файлы

• Фамилия, имя, отчество слушателя.docx

• Бизнесплан по разведению крупно рогатого скота мясного направления 2020 год.pdf

• Таырыбы Салауаттылы денсаулы кепілі Сабаты масаты.docx

• Верхняя конечность.docx

• Работа социального педагога по организации социального опыта.doc