Коммутатор последовательно считывает поступающие на его входы символы и устанавливает на выходе очередность кодовых символов в канал связи. По аналогии с блоковыми кодами, сверточные коды можно классифицировать на систематические и несистематические.



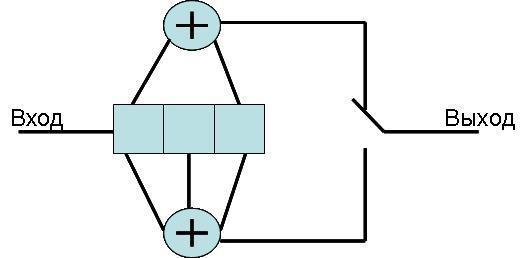
25 билет

1.Частотная модуляция (параметры, спектр).

при частотной модуляции (ЧМ или F3) амплитуда модулированного несущего колебания остается неизменной, а меняется только его частота в соответствии с изменением амплитуды первичного сигнала. На рис. 1.8 показаны формы исходного (модулирующего) и частотно-модулированного сигналов.



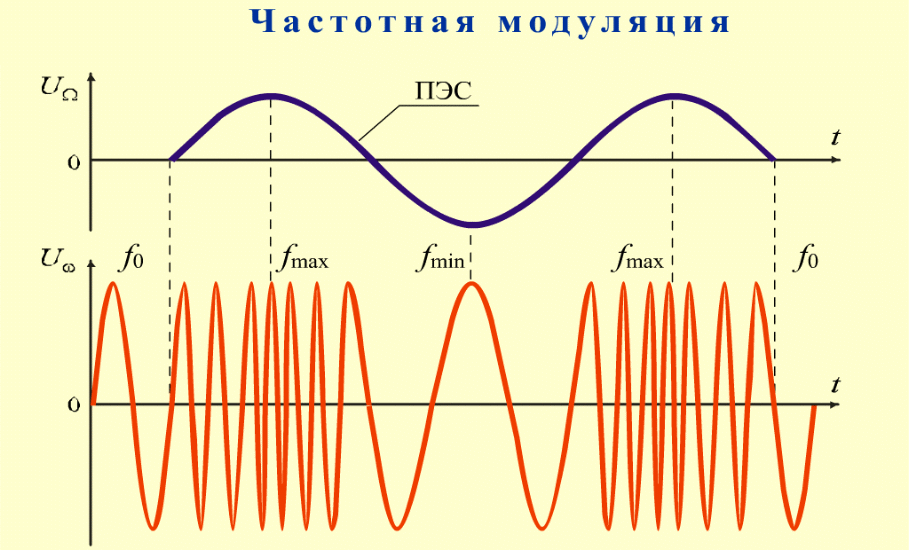
Рис. 1.8. Принцип частотной модуляции

Максимальное отклонение частоты от среднего значения несущей называется девиацией частоты:

Δωm = ωmax – ωо = ωо – ωmin ,

или

Δfm = fmax – fо = fо – fmin .

Отношение



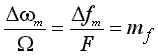
называется индексом частотной модуляции. Здесь Ω (F) – частота первичного сигнала.

Спектр при частотной модуляции выглядит следующим образом:



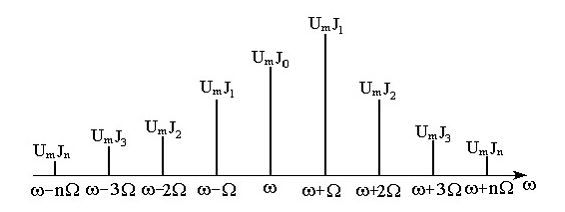
Состоит из несущей и симметрично отстающей от нее вправо и влево гармоник боковых полос, на частоту кратную частоте модулирующего колебания.
Данный спектр представляет гармоническое колебание. В случае реальной модуляции, спектр имеет более сложные очертания.
2.Регенерация сигнала ИКМ.

При прохождении по линии связи цифровой сигнал ИКМ ослабляется, искажается и подвергается воздействию различных помех, что приводит к изменению формы и длительности импульсов, уменьшению их амплитуды. Для устранения или уменьшения указанных искажении цифрового импульсного сигнала в линейном тракте на определенном расстоянии друг от друга устанавливаются регенераторы. Задача регенератора состоит в том, чтобы восстановить амплитуду, форму, длительность каждого из импульсов линейного сигнала, а также величину временного интервала между соседними импульсами.

---

Возможность регенерации линейного сигнала относительно простыми техническими средствами - одно из главных достоинств устройств связи с ИКМ. Регенерация позволяет "очистить" от помех и искажений сигнал, прошедший через участок линии связи, и восстановить его в том виде, в каком он поступил на вход этого участка. Отношение сигнал / помеха на выходе каждого из регенераторов при этом практически одинаково, т. е. аддитивные помехи и шумы, не зависящие от сигнала, подавляются в пределах участка и вдоль линии не накапливаются. Этим системы с ИКМ выгодно отличаются от аналоговых систем с частотным делением каналов, где шумы и помехи усиливаются вместе с полезным сигналом и передаются от одного усилительного пункта к другому, вдоль линейного факта, т. е. происходит накопление помех.

Процесс регенерации импульсов можно разделить на следующие операции:

• 
  1 - усиление и корректирование формы импульсов, поступающих с линии;
  
• 
  2 - выделение тактовой частоты и формирование стробирующих импульсов;
  
• 
  3 - стробирование скорректированной импульсной последовательности;
  
• 
  4 - сравнение с пороговым напряжением;
  
• 
  5 - формирование неискаженной импульсной последовательности.
  

На рис. 1 показана структурная схема регенератора однополярного сигнала, а на рис. 2 - временные диаграммы регенерации сигнала.



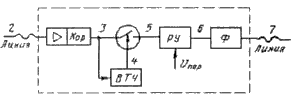
Рис. 1.

Диаграмма 1 показывает форму сигнала на выходе предыдущей станции. Искаженный сигнал, прошедший линию (2) поступает на вход усилителя-корректора. Для уменьшения межсимвольных искажений первого рода он корректирует (3). Из-за шумов в линии на cигнал наложен аддитивный шум. В выделителе тактовой частоты (ВТЧ) формируются стобирующие импульсы тактовой частоты (4). С выхода усилителя-корректора линейный сигнал поступает на ключ, где происходит его стробирование импульсами тактовой частоты. На выходе ключа получаем импульсы малой длительности, амплитуда которых из-за наличия шумов и оставшихся нескорректированных межсимвольных помех может изменяться. Далее импульсы поступают на решающее устройство РУ где их амплитуда сравнивается с пороговым напряжением Пороговое напряжение обычно выбирается равным половине амплитуды входного сигнала. Если амплитуда импульса больше порогового напряжения, то решающее устройство фиксирует на входе наличие импульса или единицы, если амплитуда импульса меньше порогового напряжения, то решающее устройство фиксирует на входе отсутствие импульса, или ноль (диаграмма 5, 6). На выходе формирователя (Ф) получается регенерированная последовательность импульсов двоичного сигнала требуемой амплитуды (диаграмма 7).

---

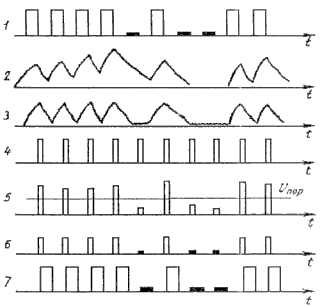
Рис. 2.
26 билет

1. 
   Функция корреляции.
   

Функция корреляции характеризует степень статистической зависимости двух значений случайного процесса, разделенных интервалом времени . (тау)

Общее определение – функция корреляции случайного процесса

B(t1,t2) это второй центральный смешанный момент распределения случайного процесса.



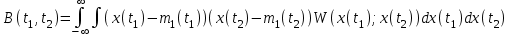
(12.1)

Для эргодического стационарного случайного процесса с нулевым средним функция корреляции зависит только от разности =(t2-t1) и определяется выражением:

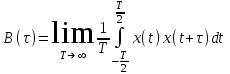(12.2)
Стандартный вид функции корреляции.

В()
В(0)

Рис.12.1.



-к 0 к 
1.В() - четная; В() = В(-)

2.В(0) - max; В(0) = ² (средняя мощность переменной составляющей, т.е. дисперсия случайного процесса).

3.

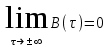
4. 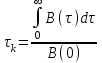интервал корреляции случайного процесса, характеризует ширину графика функции корреляции:

||  _к - то значения коррелированны,

|| > _к - то значения не коррелированны.

2. 
   R() = В() / В(0) - коэффициент корреляции, R()  1.
   

---

2.Регенерация сигнала ИКМ [р(1/0) и р(0/1)].

Регенерация – это восстановление частично пораженных помехой импульсов сигнала

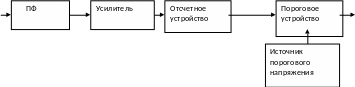
Регенерация сигнала ИКМ осуществляется регенератором (рис.2.6), на вход которого поступает процесс z(t), представляющий собой сумму сигнала и шума.

z (t) [z_n]

Рис.2.6.

В состав регенератора входят:

• 
  полосовой фильтр, выделяющий информационный сигнал, пораженный
  

помехами;

- усилитель;

• 
  отсчетное устройство, которое берет отсчеты процесса z(t) в тактовые
  

моменты времени (T/2 + kT) ;

• 
  пороговое устройство, в котором отсчеты z(T/2 + kT) сравниваются с пороговым напряжением V, поступающим от источника порогового напряжения;
  

если z(T/2 + kT) > V, то на выходе порогового устройства 1,

если z(T/2 + kT)

Т.о. на выходе отсчетного устройства получим одномерный вектор-строку [z_n], координаты которого равны отсчетам процесса z в тактовые моменты времени: [z_n]=[z(T/2), z(T/2+T)…..z(T/2+nT)].

На выходе порогового устройства получим вектор-строку, который пусть имеет вид   . Этот вектор называется оценкой информационного сигнала и координаты его, в отсутствии помех, должны быть равны переданному сигналу. Очевидно, что под действием помех некоторые импульсы искажаются и будут приняты неверно. Если приняли '0' , а была передана '1', то эта ошибка называется 'пропуск сигнала'. Вероятность принятия 0 при передаче 1 обозначим p(0/1). Если приняли '1' , а был передан '0', то эта ошибка называется 'ложная тревога'. Вероятность принятия 1 при передаче 0 обозначим p(1/0).
27 билет

1. 
   Энергетический спектр. Соотношение Винера-Хинчина.
   

Энергетическим спектром G() называется зависимость энергии составляющих случайного процесса от частоты.Стандартный вид энергетического спектра:



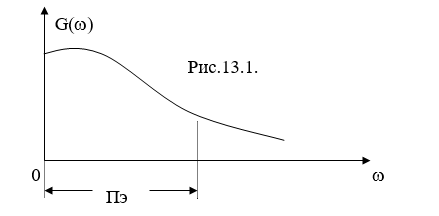
Энергетический спектр показывает, какая энергия процесса заключена в единичной полосе частот, т.е. это энергия процесса, приходящаяся на 1Гц или на 1 рад/с. Размерность G() --- В²/Гц или В²/ рад*Гц

П_э - ширина энергетического спектра,т.е. полоса частот, в пределах которой заключено порядка 95  - 99,9  энергии всего процесса. Она обратно пропорциональна интервалу корреляции

П_э = const / _к

const  3  6- зависит от ограничений накладываемых на сигнал .

• 
  Соотношение Винера-Хинчина
  

Это соотношение связывает функцию корреляции и энергетический спектр случайного процесса. В теории случайных процессов это соотношение аналогично преобразованию Фурье для детерминированных процессов:

1   2   3   4   5   6   7   8   9

---

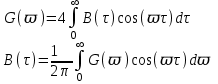(14.1)

Коэффициенты могут быть и другими.

В теории связи, в качестве модели помехи, часто используется случайный процесс, называемый белым шумом.

• 
  Применение соотношения (если попросит)
  

Белым шумом называется абсолютно случайный (дикий) процесс, энергетический спектр которого бесконечен и равномерен.



G() = G₀ при 0    

G₀ - спектральная плотность белого шума.

Мощность белого шума в полосе частот  ( в рад/с ) :

P = G₀*

Пример белого шума - это тепловой шум. Функция корреляции белого шума вычисляется в соответствии с преобразованием Винера-Хинчина:



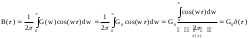
Функция корреляции белого шума имеет следующий вид:


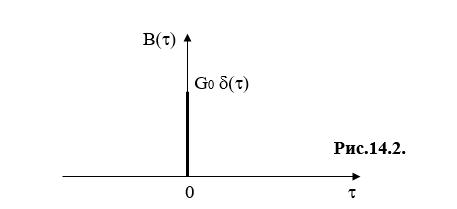
Рассмотрим прохождение белого шума через полосовой фильтр. На входе идеального полосового фильтра с АЧХ равной :



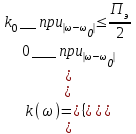
действует нормальный белый шум со спектральной плотностью G₀. Определим функцию корреляции и ФПВ процесса y на выходе фильтра; т.е. В()_вых и W(y) .

2. 
   Регенерация. Оптимальное пороговое напряжение..
   

Регенерация – это восстановление частично пораженных помехой импульсов сигнала.

Пороговое напряжение, при котором средняя вероятность ошибки минимальна, называется оптимальным пороговым напряжением V_опт . Оптимальное значение порогового напряжения может быть найдено как решение уравнения:

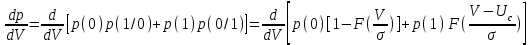=0; (2.8)

---

Смотрите также файлы

• Фамилия, имя, отчество слушателя.docx

• Бизнесплан по разведению крупно рогатого скота мясного направления 2020 год.pdf

• Таырыбы Салауаттылы денсаулы кепілі Сабаты масаты.docx

• Верхняя конечность.docx

• Работа социального педагога по организации социального опыта.doc