Тождественные преобразования

• 
  Свободно оперировать понятиями степени с целым и дробным показателем;
  
• 
  выполнять доказательство свойств степени с целыми и дробными показателями;
  
• 
  оперировать понятиями «одночлен», «многочлен», «многочлен с одной переменной», «многочлен с несколькими переменными», коэффициенты многочлена, «стандартная запись многочлена», степень одночлена и многочлена;
  
• 
  свободно владеть приемами преобразования целых и дробно-рациональных выражений;
  
• 
  выполнять разложение многочленов на множители разными способами, с использованием комбинаций различных приёмов;
  
• 
  использовать теорему Виета и теорему, обратную теореме Виета, для поиска корней квадратного трёхчлена и для решения задач, в том числе задач с параметрами на основе квадратного трёхчлена;
  
• 
  выполнять деление многочлена на многочлен с остатком;
  
• 
  доказывать свойства квадратных корней и корней степени n;
  
• 
  выполнять преобразования выражений, содержащих квадратные корни, корни степени n;
  
• 
  свободно оперировать понятиями «тождество», «тождество на множестве», «тождественное преобразование»;
  
• 
  выполнять различные преобразования выражений, содержащих модули.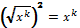
  

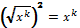
В повседневной жизни и при изучении других предметов:

• 
  выполнять преобразования и действия с буквенными выражениями, числовые коэффициенты которых записаны в стандартном виде;
  
• 
  выполнять преобразования рациональных выражений при решении задач других учебных предметов;
  
• 
  выполнять проверку правдоподобия физических и химических формул на основе сравнения размерностей и валентностей
  

Уравнения и неравенства

• 
  Свободно оперировать понятиями: уравнение, неравенство, равносильные уравнения и неравенства, уравнение, являющееся следствием другого уравнения, уравнения, равносильные на множестве, равносильные преобразования уравнений;
  
• 
  решать разные виды уравнений и неравенств и их систем, в том числе некоторые уравнения 3 и 4 степеней, дробно-рациональные и иррациональные;
  
• 
  знать теорему Виета для уравнений степени выше второй;
  
• 
  понимать смысл теорем о равносильных и неравносильных преобразованиях уравнений и уметь их доказывать;
  
• 
  владеть разными методами решения уравнений, неравенств и их систем, уметь выбирать метод решения и обосновывать свой выбор;
  
• 
  использовать метод интервалов для решения неравенств, в том числе дробно-рациональных и включающих в себя иррациональные выражения;
  
• 
  решать алгебраические уравнения и неравенства и их системы с параметрами алгебраическим и графическим методами;
  
• 
  владеть разными методами доказательства неравенств;
  
• 
  решать уравнения в целых числах;
  
• 
  изображать множества на плоскости, задаваемые уравнениями, неравенствами и их системами.
  

---

В повседневной жизни и при изучении других предметов:

• 
  составлять и решать уравнения, неравенства, их системы при решении задач других учебных предметов;
  
• 
  выполнять оценку правдоподобия результатов, получаемых при решении различных уравнений, неравенств и их систем при решении задач других учебных предметов
  
• 
  составлять и решать уравнения и неравенства с параметрами при решении задач других учебных предметов;
  
• 
  составлять уравнение, неравенство или их систему, описывающие реальную ситуацию или прикладную задачу, интерпретировать полученные результаты
  

Функции

• 
  Свободно оперировать понятиями: зависимость, функциональная зависимость, зависимая и независимая переменные, функция, способы задания функции, аргумент и значение функции, область определения и множество значения функции, нули функции, промежутки знакопостоянства, монотонность функции, наибольшее и наименьшее значения, чётность/нечётность функции, периодичность функции, график функции, вертикальная, горизонтальная, наклонная асимптоты; график зависимости, не являющейся функцией,
  
• 
  строить графики функций: линейной, квадратичной, дробно-линейной, степенной при разных значениях показателя степени, ;
  
• 
  использовать преобразования графика функции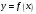 для построения графиков функций ;
  
• 
  анализировать свойства функций и вид графика в зависимости от параметров;
  
• 
  свободно оперировать понятиями: последовательность, ограниченная последовательность, монотонно возрастающая (убывающая) последовательность, предел последовательности, арифметическая прогрессия, геометрическая прогрессия, характеристическое свойство арифметической (геометрической) прогрессии;
  
• 
  использовать метод математической индукции для вывода формул, доказательства равенств и неравенств, решения задач на делимость;
  
• 
  исследовать последовательности, заданные рекуррентно;
  
• 
  решать комбинированные задачи на арифметическую и геометрическую прогрессии.
  

В повседневной жизни и при изучении других предметов:

• 
  конструировать и исследовать функции, соответствующие реальным процессам и явлениям, интерпретировать полученные результаты в соответствии со спецификой исследуемого процесса или явления;
  
• 
  использовать графики зависимостей для исследования реальных процессов и явлений;
  
• 
  конструировать и исследовать функции при решении задач других учебных предметов, интерпретировать полученные результаты в соответствии со спецификой учебного предмета
  

---

Статистика и теория вероятностей после задач

• 
  Свободно оперировать понятиями: столбчатые и круговые диаграммы, таблицы данных, среднее арифметическое, медиана, наибольшее и наименьшее значения выборки, размах выборки, дисперсия и стандартное отклонение, случайная изменчивость;
  
• 
  выбирать наиболее удобный способ представления информации, адекватный её свойствам и целям анализа;
  
• 
  вычислять числовые характеристики выборки;
  
• 
  свободно оперировать понятиями: факториал числа, перестановки, сочетания и размещения, треугольник Паскаля;
  
• 
  свободно оперировать понятиями: случайный опыт, случайный выбор, испытание, элементарное случайное событие (исход), классическое определение вероятности случайного события, операции над случайными событиями, основные комбинаторные формулы;
  
• 
  свободно оперировать понятиями: случайный опыт, случайный выбор, испытание, элементарное случайное событие (исход), классическое определение вероятности случайного события, операции над случайными событиями, основные комбинаторные формулы;
  
• 
  знать примеры случайных величин, и вычислять их статистические характеристики;
  
• 
  использовать формулы комбинаторики при решении комбинаторных задач;
  
• 
  решать задачи на вычисление вероятности в том числе с использованием формул.
  

В повседневной жизни и при изучении других предметов:

• 
  представлять информацию о реальных процессах и явлениях способом, адекватным её свойствам и цели исследования;
  
• 
  анализировать и сравнивать статистические характеристики выборок, полученных в процессе решения прикладной задачи, изучения реального явления, решения задачи из других учебных предметов;
  
• 
  оценивать вероятность реальных событий и явлений в различных ситуациях
  

Текстовые задачи

• 
  Решать простые и сложные задачи, а также задачи повышенной трудности и выделять их математическую основу;
  
• 
  распознавать разные виды и типы задач;
  
• 
  использовать разные краткие записи как модели текстов сложных задач и задач повышенной сложности для построения поисковой схемы и решения задач, выбирать оптимальную для рассматриваемой в задаче ситуации модель текста задачи;
  
• 
  различать модель текста и модель решения задачи, конструировать к одной модели решения сложных задач разные модели текста задачи;
  
• 
  знать и применять три способа поиска решения задач (от требования к условию и от условия к требованию, комбинированный);
  
• 
  моделировать рассуждения при поиске решения задач с помощью граф-схемы;
  
• 
  выделять этапы решения задачи и содержание каждого этапа;
  
• 
  уметь выбирать оптимальный метод решения задачи и осознавать выбор метода, рассматривать различные методы, находить разные решения задачи, если возможно;
  
• 
  анализировать затруднения при решении задач;
  
• 
  выполнять различные преобразования предложенной задачи, конструировать новые задачи из данной, в том числе обратные;
  
• 
  интерпретировать вычислительные результаты в задаче, исследовать полученное решение задачи;
  
• 
  изменять условие задач (количественные или качественные данные), исследовать измененное преобразованное;
  
• 
  анализировать всевозможные ситуации взаимного расположения двух объектов и изменение их характеристик при совместном движении (скорость, время, расстояние).при решение задач на движение двух объектов как в одном, так и в противоположных направлениях, конструировать новые ситуации на основе изменения условий задачи при движении по реке;
  
• 
  исследовать всевозможные ситуации при решении задач на движение по реке, рассматривать разные системы отсчёта;
  
• 
  решать разнообразные задачи «на части»;
  
• 
  решать и обосновывать свое решение задач (выделять математическую основу) на нахождение части числа и числа по его части на основе конкретного смысла дроби;
  
• 
  объяснять идентичность задач разных типов, связывающих три величины (на работу, на покупки, на движение). выделять эти величины и отношения между ними, применять их при решении задач, конструировать собственные задач указанных типов;
  

---

• 
  владеть основными методами решения задач на смеси, сплавы, концентрации, использовать их в новых ситуациях по отношению к изученным в процессе обучения;
  

• 
  решать задачи на проценты, в том числе, сложные проценты с обоснованием, используя разные способы;
  
• 
  решать логические задачи разными способами, в том числе, с двумя блоками и с тремя блоками данных с помощью таблиц;
  
• 
  решать задачи по комбинаторике и теории вероятностей на основе использования изученных методов и обосновывать решение;
  
• 
  решать несложные задачи по математической статистике;
  
• 
  овладеть основными методами решения сюжетных задач: арифметический, алгебраический, перебор вариантов, геометрический, графический, применять их в новых по сравнению с изученными ситуациях.
  

В повседневной жизни и при изучении других предметов:

• 
  конструировать новые для данной задачи задачные ситуации с учётом реальных характеристик, в частности, при решении задач на концентрации, учитывать плотность вещества; решать и конструировать задачи на основе рассмотрения реальных ситуаций, в которых не требуется точный вычислительный результат;
  
• 
  решать задачи на движение по реке, рассматривая разные системы отсчёта;
  
• 
  конструировать задачные ситуации, приближенные к реальной действительности
  

Геометрические фигуры

• 
  Свободно оперировать геометрическими понятиями при решении задач и проведении математических рассуждений;
  
• 
  самостоятельно формулировать определения геометрических фигур, выдвигать гипотезы о новых свойствах и признаках геометрических фигур и обосновывать или опровергать их, обобщать или конкретизировать результаты на новые классы фигур, проводить в несложных случаях классификацию фигур по различным основаниям;
  
• 
  исследовать чертежи, включая комбинации фигур, извлекать, интерпретировать и преобразовывать информацию, представленную на чертежах;
  
• 
  решать задачи геометрического содержания, в том числе в ситуациях, когда алгоритм решения не следует явно из условия, выполнять необходимые для решения задачи дополнительные построения, исследовать возможность применения теорем и формул для решения задач;
  
• 
  формулировать и доказывать геометрические утверждения.
  

В повседневной жизни и при изучении других предметов:

• 
  составлять с использованием свойств геометрических фигур математические модели для решения задач практического характера и задач из смежных дисциплин, исследовать полученные модели и интерпретировать результат
  

---

Отношения

• 
  Владеть понятием отношения как метапредметным;
  
• 
  свободно оперировать понятиями: равенство фигур, равные фигуры, равенство треугольников, параллельность прямых, перпендикулярность прямых, углы между прямыми, перпендикуляр, наклонная, проекция, подобие фигур, подобные фигуры, подобные треугольники;
  
• 
  использовать свойства подобия и равенства фигур при решении задач.
  

В повседневной жизни и при изучении других предметов:

• 
  использовать отношения для построения и исследования математических моделей объектов реальной жизни
  

Измерения и вычисления

• 
  Свободно оперировать понятиями длина, площадь, объём, величина угла как величинами, использовать равновеликость и равносоставленность при решении задач на вычисление, самостоятельно получать и использовать формулы для вычислений площадей и объёмов фигур, свободно оперировать широким набором формул на вычисление при решении сложных задач, в том числе и задач на вычисление в комбинациях окружности и треугольника, окружности и четырёхугольника, а также с применением тригонометрии;
  
• 
  самостоятельно формулировать гипотезы и проверять их достоверность.
  

В повседневной жизни и при изучении других предметов:

• 
  свободно оперировать формулами при решении задач в других учебных предметах и при проведении необходимых вычислений в реальной жизни
  

Геометрические построения

• 
  Оперировать понятием набора элементов, определяющих геометрическую фигуру,
  
• 
  владеть набором методов построений циркулем и линейкой;
  
• 
  проводить анализ и реализовывать этапы решения задач на построение.
  

В повседневной жизни и при изучении других предметов:

• 
  выполнять построения на местности;
  
• 
  оценивать размеры реальных объектов окружающего мира
  

Преобразования

• 
  Оперировать движениями и преобразованиями как метапредметными понятиями;
  
• 
  оперировать понятием движения и преобразования подобия для обоснований, свободно владеть приемами построения фигур с помощью движений и преобразования подобия, а также комбинациями движений, движений и преобразований;
  
• 
  использовать свойства движений и преобразований для проведения обоснования и доказательства утверждений в геометрии и других учебных предметах;
  
  • 
    пользоваться свойствами движений и преобразований при решении задач.
    

---

Смотрите также файлы

• Директор инспо канд пед наук, доцент Т. П. Хлопова (подпись) 2023 г. Выпускная квалификационная работа (дипломная работа) рекреационное развитие ростовской области.docx

• Лабораторная работа 1 Основы работы в сапр компас3D v20. Режим Эскиз цель знакомство с интерфейсом компас3D v20.docx

• Юридический институт проблема нехватки молодых специалистов на государственной и муниципальной службе.docx

• Профильспециализация Управление проектами.docx

• Работы аутизм. Расстройства аутистического спектра.pdf