ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 41
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ушел из жизни. Местом его захоронения стала парижская приходская церковь Сен-Этьен-дю-Мон. Судить о жизни и творчестве Паскаля, о его личности можно по эпитафии, которая была произнесена одним из ученых: «Поистине можно сказать, что мы потеряли один из самых больших умов, которые когда-либо существовали. Я не вижу никого, с кем можно было бы его сравнить: Пико делла Мирандола и все эти люди, которыми восхищался свет, были глупцами возле него… Тот, о ком мы скорбим, был королем в королевстве умов».
Открытия Паскаля до сегодняшнего дня служат в сфере гидравлики и вычислительной техники

Рисунок 3 – Место захоронения Б.Паскаля
2 Первые работы
Первое знаменательное событие в биографии молодого ученого случилось в 1640 году, когда ему исполнилось всего 17 лет. Паскаль издал свой первый трактат под названием «Опыт теории конических сечений» (рисунок 2), ставший основой для дальнейших разработок в геометрии. Третью лемму этого трактата назвали в честь ее создателя – теорема Паскаля. С ее помощью можно по пяти точкам построить каноническое сечение.
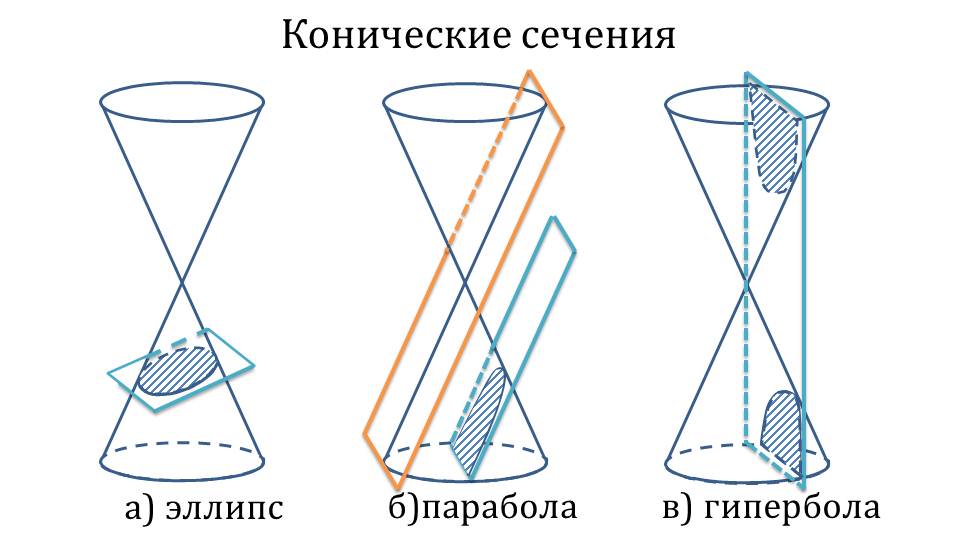
Рисунок 4 – Трактат «Опыт теории конических сечений»
В это сочинение автор включил теоремы (доказательства не приводятся), три определения, три леммы и указал главы планируемого труда, посвящённого коническим сечениям. Третья лемма из «Опыта…» является теоремой Паскаля: если вершины шестиугольника лежат на некотором коническом сечении, то три точки пересечения прямых, содержащих противоположные стороны, лежат на одной прямой. Этот результат и 400 следствий из него Паскаль изложил в «Полном труде о конических сечениях», о завершении которого Паскаль сообщил пятнадцать лет спустя и который сейчас отнесли бы к проективной геометрии. «Полный труд…» так и не был опубликован: в 1675 году его прочёл в рукописи Лейбниц, рекомендовавший племяннику Паскаля Этьену Перье срочно напечатать его. Однако Перье не прислушался к мнению Лейбница и впоследствии рукопись была утеряна.
3 Счетная суммирующая машина Паскаля
Счетная суммирующая машина Блеза Паскаля – это изобретение, удивившее современников, но так и не нашедшее свой круг клиентов. Механизм, в основе имеющий зубчатые колесики, считается одним из прародителей калькулятора.
Паскаль уже в 19-летнем возрасте начал заниматься разработкой своей счетной машины, о которой сейчас можно прочитать на страницах учебников. Это изобретение считается одним из прообразов калькулятора.
«Паскалина» (рисунок 5) - это небольшой ящичек, в котором находится множество соединенных между собой зубчатых колесиков (шестеренок). На каждом колесике были разметки от нуля до девяти. Для того, чтобы произвести операцию сложения необходимо было набрать суммирующиеся числа с помощью нужного количества оборотов шестеренок. Колесики двигались до того момента, пока не появилось нужное число. При полном обороте появившейся остаток (больше 9) шестеренка перекидывала на другой разряд, передвигая соседнее колесо на одно деление.

Рисунок 5 - Паскалина
В данной вычислительной машине колеса могли вращаться только в одном направлении. Производить суммирующие операции на такой машине было легко. Например, нам необходимо высчитать сумму 10+15=? Для этого необходимо вращать колесо пока не выставится значение первого слагаемого 10, потом крутим это же колесо до значения 15. При этом указатель сразу же показывает 25. То есть подсчет происходит в полуавтоматическом режиме.
Вычитание на такой машине невозможно произвести, так как колеса не вращаются в обратном направлении. Делить и умножать арифмометр Паскаля не умел. Но даже в таком виде и с такими функциональными возможностями эта машина была полезной и ей с радостью пользовался Паскаль-старший. Машина производила быстрые и безошибочные математические действия по суммированию вложил.
Использование оборотов колеса для процесса сложения не был новшеством в научной деятельности Паскаля, так как эту идею озвучил еще в 1623 году Вильгельм Шиккард. А действительно изобретением Блеза считается перенос остатка в следующий разряд при полном вращении шестеренки.
В первых «паскалинах» было по пять зубчатых колесиков, а уже с дальнейшей модернизацией технологии в механизме их число доходило до восьми штук, что позволяло работать с большими числами (до 9999999).
Этот механизм активно использовался в разных технических приборах до ХХ века. Его преимуществом было умение автоматического складывания многозначных чисел самим прибором.
Исследователи истории возникновения счетных механизмов считают, что Паскаль создал свою суммирующую машину практически с нуля, так как не был ознакомлен с проектом Шиккарда.
В 18 столетии арифмометры Паскаля широко использовались моряками, артиллеристами и ученными для арифметических сложений.
Прибор удивил современную науку, однако из-за высокой стоимости и сложности в эксплуатации так и не смог обрести свою аудиторию. Все же изобретение Паскаля внесло огромный вклад в историю развития вычислительной техники.
4 Треугольник Паскаля и его свойства
Треугольник Паскаля арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля.
Если очертить треугольник Паскаля (рисунок 6), то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Продолжать треугольник можно бесконечно. Строки треугольника симметричны относительно вертикальной оси. Имеет применение в теории вероятности и обладает занимательными свойствами.

Рисунок 6 – Треугольник Паскаля
Мартин Гарднер пишет в книге «Математические новеллы» (М., Мир, 1974): «Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике».
Треугольник Паскаля обладает следующими свойствами (рисунок 6)
Второе число каждой строки соответствует её номеру.
Третье число каждой строки равно сумме номеров строк, ей предшествующих.
Четвертое число каждой строки является тетраэдрическим.
Если вычесть из центрального числа в строке с чётным номером соседнее число из той же строки, то получится число Каталана.
Сумма чисел n-й строки треугольника Паскаля равна 2n
Простые делители чисел треугольника Паскаля образуют симметричные самоподобные структуры.

Рисунок 7 -Свойства треугольника
Треугольные числа в самом обычном и привычном нам виде показывают, сколько касающихся кружков можно расположить в виде треугольника - как классический пример начальная расстановка шаров в бильярде. К одной монетке можно прислонить еще две - итого три - к двум можно приладить еще три - итого шесть. Продолжая наращивать ряды с сохранением формы треугольника, получим ряд 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66..., что и показывает вторая зеленая линия. Этот замечательный ряд, каждый член которого равен сумме натурального ряда чисел (55=1+2+3+4+5+6+7+8+9+10), содержит также множество знакомцев, хорошо известных любителям математики: 6 и 28 - совершенные числа, 36 - квадратное число, 8 и 21 - числа Фибоначчи.
Биномиальные коэффициенты есть коэффициенты разложения многочлена по степеням x и y.
Каждая строчка имеет определенную структуру:
В треугольнике представлены коэффициенты в разложении (a+b)n (рисунок 6). Номер строчки в этом треугольнике соответствует n+1. Теперь разберемся со степенями одночленов в разложении.
Степени всех одночленов, входящих в состав разложения равны n, причем степень первого слагаемого a уменьшается с n до 0, а степень второго слагаемого b увеличивается с 0 до n. Коэффициенты разложения совпадают с числами, стоящими в пятой строчке треугольника Паскаля.
Пользуясь треугольником Паскаля, мы можем возвести двучлен (a+b) в любую степень, не заучивая сложные формулы.
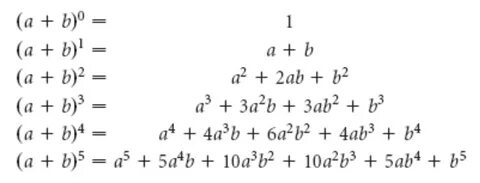
Рисунок 8 – Возведение многочлена в степень
5 Вклад Паскаля в физику
Физикой Паскаль начал увлекаться в 1646 году, когда он узнал о трубке, которую изобрел Торричели. Блез начал проводить опыты и эксперименты, стремясь доказать на практике, что гипотеза Аристотеля о «боязне пустоты» ограничена определенными пределами. Проводя опыты с трубкой Торичелли – сосудом, заполненным ртутью – он доказал существование атмосферного давления, подтвердив существовавшие ранее гипотезы. Сам Паскаль писал, что с помощью такого прибора можно было бы узнать, как две разных точки земного шара смещены относительно друг друга. Эти исследования стали важным этапом усовершенствования барометров.
Продолжая развивать работы Симона Стевина и Галилео Галилея, Паскаль сформулировал закон о распределении давления в жидкой среде, получивший затем его имя. Выведенное им уравнение служит основой гидростатики. Кроме того, в своем трактате «О равновесии жидкостей» Блез впервые опубликовал идею гидравлического пресса. Изобретение долгое время оставалось невостребованным, и только в 1975 году английский инженер Джозеф Брама запатентовал прототип устройства.
Занимаясь проблемами физики, ученый сформулировал закон, который в настоящее время носит имя «закон Паскаля». В честь Блеза Паскаля была названа физическая единица 1Паскаль - единица измерения давления. Опыты Паскаля 1647 г. со столбами различных жидкостей доказали существование атмосферного давления. Для проведения опытов Паскалю понадобилась помощь искусных стеклодувов, много вина, масла и воды и в придачу трехмачтовое судно, причем даже неизвестно, потребовалось ли этому судну отходить от причала. Ведь для опытов с этими жидкостями ученому были необходимы трубки длиной около 15 м, которые поддерживались в вертикальном положении привязанными к мачтам. В ходе проведенных экспериментов Паскалю удалось изобрести шприц и гидравлический пресс и усовершенствовать барометр. Увлекшись философией, Блез Паскаль продолжил учение Декарта о методе логического мышления, в «Письмах к провинциалу» остро критиковал иезуитов, склонялся к превосходству веры над разумом. Основное его философское сочинение «Мысли о религии» было издано в 1669 году. Блез Паскаль сравнивал Вселенную со сферой. Он писал о Вселенной как о не имеющей границ сфере, центр которой всюду, поверхность – нигде! Блез Паскаль считал, что эти три состояния разума и души могут описать отношение человека к любому явлению или к любой информации. Это - вера, отрицание и сомнение. Блез Паскаль писал: «Самые лучшие книги - те, при чтении которых каждый верил бы, что сам бы мог их написать». Паскаль утверждал, что человек никогда не сможет стать счастливым, так как « мы никогда не живем, мы только надеемся жить и постоянно надеемся быть такими». Блез Паскаль говаривал: «Величие человека тем и велико, что он сознает свое ничтожество». Блез Паскаль говорил: «Не огромность мира звезд вызывает восхищение, а человек который этот мир измерил». Паскаль считает, что есть только три типа людей: одни обрели Бога и служат ему - эти люди разумны и счастливы. Другие же не нашли и не ищут Его - эти безумны и несчастны. Третьи не обрели, но ищут Его - эти люди разумны, но еще несчастны». Блез Паскаль назвал молчание «величайшим из человеческих страданий». Многие выдающиеся ученые прошлого стремились создать вечный двигатель. Не избежал этой участи и великий Блез Паскаль. Он рассматривал в качестве прообраза вечного двигателя груз, движущийся по тяжелому вращающемуся маховику. Однако в отличие от большинства других проектов перпетуум-мобиле, разработка Паскаля нашла выход в практику, правда, не для тех целей, для которых ее создавал автор. Это – рулетка казино. Паскаль, много занимавшийся теорией азартных игр, вывел «формулу игрока».
Открытия Паскаля до сегодняшнего дня служат в сфере гидравлики и вычислительной техники

Рисунок 3 – Место захоронения Б.Паскаля
2 Первые работы
Первое знаменательное событие в биографии молодого ученого случилось в 1640 году, когда ему исполнилось всего 17 лет. Паскаль издал свой первый трактат под названием «Опыт теории конических сечений» (рисунок 2), ставший основой для дальнейших разработок в геометрии. Третью лемму этого трактата назвали в честь ее создателя – теорема Паскаля. С ее помощью можно по пяти точкам построить каноническое сечение.

Рисунок 4 – Трактат «Опыт теории конических сечений»
В это сочинение автор включил теоремы (доказательства не приводятся), три определения, три леммы и указал главы планируемого труда, посвящённого коническим сечениям. Третья лемма из «Опыта…» является теоремой Паскаля: если вершины шестиугольника лежат на некотором коническом сечении, то три точки пересечения прямых, содержащих противоположные стороны, лежат на одной прямой. Этот результат и 400 следствий из него Паскаль изложил в «Полном труде о конических сечениях», о завершении которого Паскаль сообщил пятнадцать лет спустя и который сейчас отнесли бы к проективной геометрии. «Полный труд…» так и не был опубликован: в 1675 году его прочёл в рукописи Лейбниц, рекомендовавший племяннику Паскаля Этьену Перье срочно напечатать его. Однако Перье не прислушался к мнению Лейбница и впоследствии рукопись была утеряна.
3 Счетная суммирующая машина Паскаля
Счетная суммирующая машина Блеза Паскаля – это изобретение, удивившее современников, но так и не нашедшее свой круг клиентов. Механизм, в основе имеющий зубчатые колесики, считается одним из прародителей калькулятора.
Паскаль уже в 19-летнем возрасте начал заниматься разработкой своей счетной машины, о которой сейчас можно прочитать на страницах учебников. Это изобретение считается одним из прообразов калькулятора.
«Паскалина» (рисунок 5) - это небольшой ящичек, в котором находится множество соединенных между собой зубчатых колесиков (шестеренок). На каждом колесике были разметки от нуля до девяти. Для того, чтобы произвести операцию сложения необходимо было набрать суммирующиеся числа с помощью нужного количества оборотов шестеренок. Колесики двигались до того момента, пока не появилось нужное число. При полном обороте появившейся остаток (больше 9) шестеренка перекидывала на другой разряд, передвигая соседнее колесо на одно деление.

Рисунок 5 - Паскалина
В данной вычислительной машине колеса могли вращаться только в одном направлении. Производить суммирующие операции на такой машине было легко. Например, нам необходимо высчитать сумму 10+15=? Для этого необходимо вращать колесо пока не выставится значение первого слагаемого 10, потом крутим это же колесо до значения 15. При этом указатель сразу же показывает 25. То есть подсчет происходит в полуавтоматическом режиме.
Вычитание на такой машине невозможно произвести, так как колеса не вращаются в обратном направлении. Делить и умножать арифмометр Паскаля не умел. Но даже в таком виде и с такими функциональными возможностями эта машина была полезной и ей с радостью пользовался Паскаль-старший. Машина производила быстрые и безошибочные математические действия по суммированию вложил.
Использование оборотов колеса для процесса сложения не был новшеством в научной деятельности Паскаля, так как эту идею озвучил еще в 1623 году Вильгельм Шиккард. А действительно изобретением Блеза считается перенос остатка в следующий разряд при полном вращении шестеренки.
В первых «паскалинах» было по пять зубчатых колесиков, а уже с дальнейшей модернизацией технологии в механизме их число доходило до восьми штук, что позволяло работать с большими числами (до 9999999).
Этот механизм активно использовался в разных технических приборах до ХХ века. Его преимуществом было умение автоматического складывания многозначных чисел самим прибором.
Исследователи истории возникновения счетных механизмов считают, что Паскаль создал свою суммирующую машину практически с нуля, так как не был ознакомлен с проектом Шиккарда.
В 18 столетии арифмометры Паскаля широко использовались моряками, артиллеристами и ученными для арифметических сложений.
Прибор удивил современную науку, однако из-за высокой стоимости и сложности в эксплуатации так и не смог обрести свою аудиторию. Все же изобретение Паскаля внесло огромный вклад в историю развития вычислительной техники.
4 Треугольник Паскаля и его свойства
Треугольник Паскаля арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля.
Если очертить треугольник Паскаля (рисунок 6), то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Продолжать треугольник можно бесконечно. Строки треугольника симметричны относительно вертикальной оси. Имеет применение в теории вероятности и обладает занимательными свойствами.

Рисунок 6 – Треугольник Паскаля
Мартин Гарднер пишет в книге «Математические новеллы» (М., Мир, 1974): «Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике».
Треугольник Паскаля обладает следующими свойствами (рисунок 6)
Второе число каждой строки соответствует её номеру.
Третье число каждой строки равно сумме номеров строк, ей предшествующих.
Четвертое число каждой строки является тетраэдрическим.
Если вычесть из центрального числа в строке с чётным номером соседнее число из той же строки, то получится число Каталана.
Сумма чисел n-й строки треугольника Паскаля равна 2n
Простые делители чисел треугольника Паскаля образуют симметричные самоподобные структуры.

Рисунок 7 -Свойства треугольника
Треугольные числа в самом обычном и привычном нам виде показывают, сколько касающихся кружков можно расположить в виде треугольника - как классический пример начальная расстановка шаров в бильярде. К одной монетке можно прислонить еще две - итого три - к двум можно приладить еще три - итого шесть. Продолжая наращивать ряды с сохранением формы треугольника, получим ряд 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66..., что и показывает вторая зеленая линия. Этот замечательный ряд, каждый член которого равен сумме натурального ряда чисел (55=1+2+3+4+5+6+7+8+9+10), содержит также множество знакомцев, хорошо известных любителям математики: 6 и 28 - совершенные числа, 36 - квадратное число, 8 и 21 - числа Фибоначчи.
Биномиальные коэффициенты есть коэффициенты разложения многочлена по степеням x и y.
Каждая строчка имеет определенную структуру:
-
по краям стоят единицы -
количество элементов в каждой строчке равно номеру строчки -
каждый элемент строчки, кроме стоящих по краям равен сумме двух стоящих над ним.
В треугольнике представлены коэффициенты в разложении (a+b)n (рисунок 6). Номер строчки в этом треугольнике соответствует n+1. Теперь разберемся со степенями одночленов в разложении.
Степени всех одночленов, входящих в состав разложения равны n, причем степень первого слагаемого a уменьшается с n до 0, а степень второго слагаемого b увеличивается с 0 до n. Коэффициенты разложения совпадают с числами, стоящими в пятой строчке треугольника Паскаля.
Пользуясь треугольником Паскаля, мы можем возвести двучлен (a+b) в любую степень, не заучивая сложные формулы.
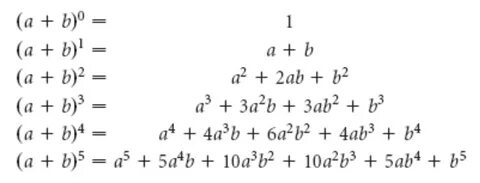
Рисунок 8 – Возведение многочлена в степень
5 Вклад Паскаля в физику
Физикой Паскаль начал увлекаться в 1646 году, когда он узнал о трубке, которую изобрел Торричели. Блез начал проводить опыты и эксперименты, стремясь доказать на практике, что гипотеза Аристотеля о «боязне пустоты» ограничена определенными пределами. Проводя опыты с трубкой Торичелли – сосудом, заполненным ртутью – он доказал существование атмосферного давления, подтвердив существовавшие ранее гипотезы. Сам Паскаль писал, что с помощью такого прибора можно было бы узнать, как две разных точки земного шара смещены относительно друг друга. Эти исследования стали важным этапом усовершенствования барометров.
Продолжая развивать работы Симона Стевина и Галилео Галилея, Паскаль сформулировал закон о распределении давления в жидкой среде, получивший затем его имя. Выведенное им уравнение служит основой гидростатики. Кроме того, в своем трактате «О равновесии жидкостей» Блез впервые опубликовал идею гидравлического пресса. Изобретение долгое время оставалось невостребованным, и только в 1975 году английский инженер Джозеф Брама запатентовал прототип устройства.
Занимаясь проблемами физики, ученый сформулировал закон, который в настоящее время носит имя «закон Паскаля». В честь Блеза Паскаля была названа физическая единица 1Паскаль - единица измерения давления. Опыты Паскаля 1647 г. со столбами различных жидкостей доказали существование атмосферного давления. Для проведения опытов Паскалю понадобилась помощь искусных стеклодувов, много вина, масла и воды и в придачу трехмачтовое судно, причем даже неизвестно, потребовалось ли этому судну отходить от причала. Ведь для опытов с этими жидкостями ученому были необходимы трубки длиной около 15 м, которые поддерживались в вертикальном положении привязанными к мачтам. В ходе проведенных экспериментов Паскалю удалось изобрести шприц и гидравлический пресс и усовершенствовать барометр. Увлекшись философией, Блез Паскаль продолжил учение Декарта о методе логического мышления, в «Письмах к провинциалу» остро критиковал иезуитов, склонялся к превосходству веры над разумом. Основное его философское сочинение «Мысли о религии» было издано в 1669 году. Блез Паскаль сравнивал Вселенную со сферой. Он писал о Вселенной как о не имеющей границ сфере, центр которой всюду, поверхность – нигде! Блез Паскаль считал, что эти три состояния разума и души могут описать отношение человека к любому явлению или к любой информации. Это - вера, отрицание и сомнение. Блез Паскаль писал: «Самые лучшие книги - те, при чтении которых каждый верил бы, что сам бы мог их написать». Паскаль утверждал, что человек никогда не сможет стать счастливым, так как « мы никогда не живем, мы только надеемся жить и постоянно надеемся быть такими». Блез Паскаль говаривал: «Величие человека тем и велико, что он сознает свое ничтожество». Блез Паскаль говорил: «Не огромность мира звезд вызывает восхищение, а человек который этот мир измерил». Паскаль считает, что есть только три типа людей: одни обрели Бога и служат ему - эти люди разумны и счастливы. Другие же не нашли и не ищут Его - эти безумны и несчастны. Третьи не обрели, но ищут Его - эти люди разумны, но еще несчастны». Блез Паскаль назвал молчание «величайшим из человеческих страданий». Многие выдающиеся ученые прошлого стремились создать вечный двигатель. Не избежал этой участи и великий Блез Паскаль. Он рассматривал в качестве прообраза вечного двигателя груз, движущийся по тяжелому вращающемуся маховику. Однако в отличие от большинства других проектов перпетуум-мобиле, разработка Паскаля нашла выход в практику, правда, не для тех целей, для которых ее создавал автор. Это – рулетка казино. Паскаль, много занимавшийся теорией азартных игр, вывел «формулу игрока».