Файл: Северокавказская государственная гуманитарнотехнологическая академия.doc
Добавлен: 22.11.2023
Просмотров: 118
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
токов и напряжений на участках цепи, не подвергшихся преобразованию. Наиболее распространенные и часто употребляемые преобразования цепей сводятся к следующим.
1. Замена последовательных сопротивлений одним эквивалентным. Эквивалентное сопротивление R цепи, состоящей из последовательно соединенных сопротивлений R1, R2,…,.Rn, равно сумме этих сопротивлений:
R= R1+ R2+…+Rn(4)
2. Замена параллельных сопротивлений одним эквивалентным. Сопротивления параллельны, если все они присоединены к одной паре узлов. Эквивалентное сопротивление R цепи, состоящей из ряда параллельно соединенных сопротивлений, определяется из формулы суммирования проводимостей: l/R=l/ R1+l/ R2+...+l/ Rn (5)
В случае двух параллельно соединенных сопротивлений R=R1·R2/(R1+R2).
3. Преобразование треугольника сопротивлений (рис. 5, а) в эквивалентную звезду сопротивлений (рис. 5, б) и наоборот. Формулы преобразований имеют следующий вид:
R1=R12 R31/A; R2=R23 R12/A; R3=R31 R23/A;
R12=R1+R2+R1 R2/R3;
R23=R2+ R3+R2 R3/R1;
R31=R3+R1+R3 R1/R2,
где A=R12+R23+R13.
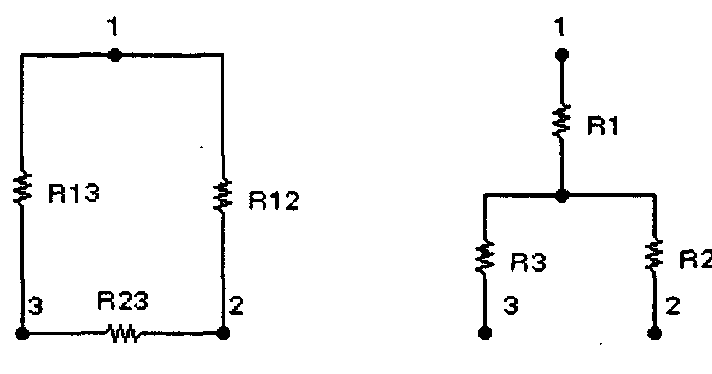
а) б)
Рис. 5. Включение сопротивлений треугольником (а) и звездой (б)
Вернемся к методу наложения и рассмотрим его применение для схемы на рис. 3.6. В этой схеме все источники напряжения идеальны, поэтому их внутренние сопротивления равны нулю. Предположим, что действует только ЭДС Е1, а вместо Е2 будет просто проводник (короткое замыкание). В этом случае ЭДС Е1 нагружена на эквивалентное сопротивление
R1экв=R2·R6/(R3+R6)+R4·R5/(R4+R5)=8 Ом.
При этом токи в ветвях составят:
I1'=E1/R1экв =96/8=12 A;
I3'=I1’·R6/(R3+R6)=12·6/9=8 A;
I4'=I1’·R5/(R4+R5)=12·10/25=4,8A;
I2'=I3’-I4'=8-4,8=3,2 A;
I6'=I1’-I3'=12-8=4 А;
I5'=I1’-14'=12-4.8=7,2 А.
Перейдем ко второму этапу, когда активной является ЭДС Е2, а Е1 — закорочена. В этом случае ЭДС Е2 нагружена на эквивалентное сопротивление R2экв=R3*R4/(R3+R4)+R5*R6/(
R5+R6)=6,25 Ом. При этом токи в ветвях имеют следующие значения;
I2"=E2/R2экв =75/2,5=12 A;
I3"=I2"·R4/(R3+R4)=12·15/18==10A;
I6"=I2"·R5/(R5+R6)=12·10/16=7,5A;
I1"=I3"-I6"=10- 7,5=2,5 А;
I4"=I2"-I3"=12-10==2 A;
I5"=I2"-I6"=12-7,5=4,5 A.
Складывая алгебраически токи, полученные от действия каждой ЭДС в отдельности, найдем истинные токи в каждой ветви:
I1=I1'-I1”=12+2,5=14,5 А;
I2=I2'+I2"=3,2+12=15,2 А;
I3=I3'+I3"=8+10=18 A;
I4=I4'-I4"=4,8-2=2,8A;
I5=I5'+I5"=7,2+4,5=11,7 A;
I6=I6"-I6'=7,5-4=2,5A,
что совпадает с результатами моделирования.
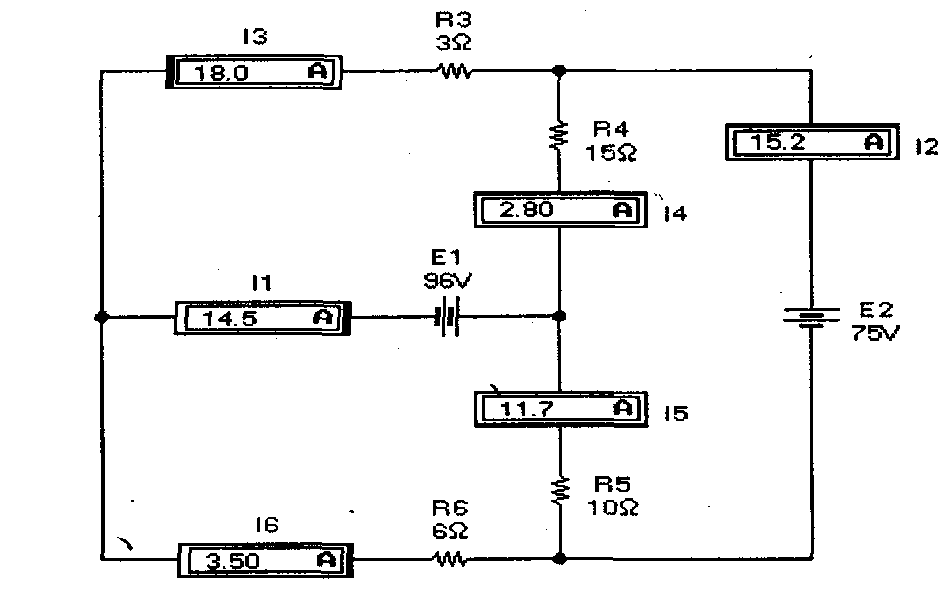
Рис. 6. Схема многоконтурной цепи
Метод эквивалентного генератора
Метод эквивалентного генератора напряжения называют иногда методом короткого замыкания и холостого хода или методом активного двухполюсника. С его помощью определяется ток в определенной ветви схемы. Назовем ее АВ и предположим, что она содержит одно сопротивление R. Для нахождения тока в этой ветви размыкают ветвь и любым из рассмотренных выше методов определяют разность потенциалов Uxx на зажимах А, В разомкнутой ветви (режим холостого хода). Затем вычисляется сопротивление короткого замыкания Rкз равное эквивалентному сопротивлению остальной цепи. При этом имеющиеся в схеме источники должны быть выключены и заменены их внутренними сопротивлениями, а питание схемы осуществляется от постороннего источника, подключенного к зажимам А, В исследуемой ветви. Следующим этапом является режим короткого замыкания, при котором определяется ток Iкз в ветви АВ при закороченных зажимах А, В. Заметим, что этот этап не обязателен, если сопротивление Rкз удалось определить другим, более простым способом. Если же режим короткого замыкания все-таки пришлось применить, то в этом случае
Rкз = Uxx / Iкз (6)
и искомый ток в ветви определяется из выражения:
I= Uxx /(R+ Rкз) (7)
Перейдем к конкретному примеру. Для этого воспользуемся схемой на рис. 7, которая представляет собой мостовую схему из двух плеч, образованных резисторами Rl, R2, RЗ, R4. В одну диагональ моста включен идеальный источник напряжения Е и переключатель, управляемый клавишей Е клавиатуры.
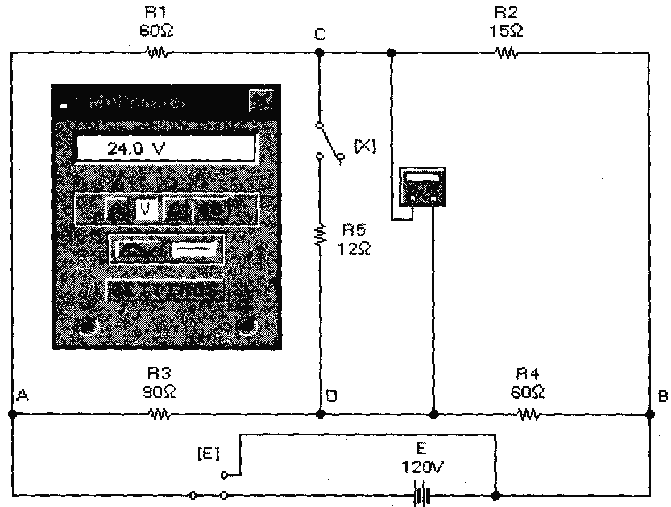
Рис. 7. Мостовая схема в режиме холостого хода
В другую диагональ моста включен резистор R5 с ключом X, который управляется одноименной клавишей. Нашей задачей является определение тока через резистор R5 в рабочем состоянии, когда ключ Х замкнут. В положении ключа X, показанном на схеме (ключ разомкнут), реализуется первый этап моделирования — режим холостого хода ветви CD. В этом режиме через сопротивления Rl, R2 протекает ток I', а через сопротивления R3, R4 — ток I", которые равны соответственно I’=E/(Rl
+R2)=120/75=l,6A;
I”=E/(R3+R4)=120/150=0,8A.
При этом потенциалы в точках С и D определяются падениями напряжений на резисторах Rl и R3: Uac=I’Rl=l,6*60=96B;
Uad=I''RЗ=0,8 *90=72 В.
Располагая потенциалами точек С и D, нетрудно найти и напряжение между ними, которое равно напряжению холостого хода:
Ucd = Uxx = Uac - Uad =96-72=24 В,
что соответствует показаниям мультиметра на рис. 7.
Теперь найдем сопротивление короткого замыкания. Как отмечалось выше, сделать это можно двумя способами.
1. Путем непосредственного расчета с использованием данных схемы. В этом случае источник Е нужно выключить, оставив его внутреннее сопротивление, равное в данном случае нулю. Сопротивление короткого замыкания будет равно сопротивлению цепи между точками С и D:
Rкз=R1*R2/(R1+R2)+R3*R4/(R3+R4).
При моделировании на схеме рис. 7 необходимо ключ Е перевести в другое положение, а мультиметр — в режим омметра. Результаты таких действий показаны на рис. 8, откуда видно, что результаты проведенного расчета полностью подтверждаются результатами моделирования.
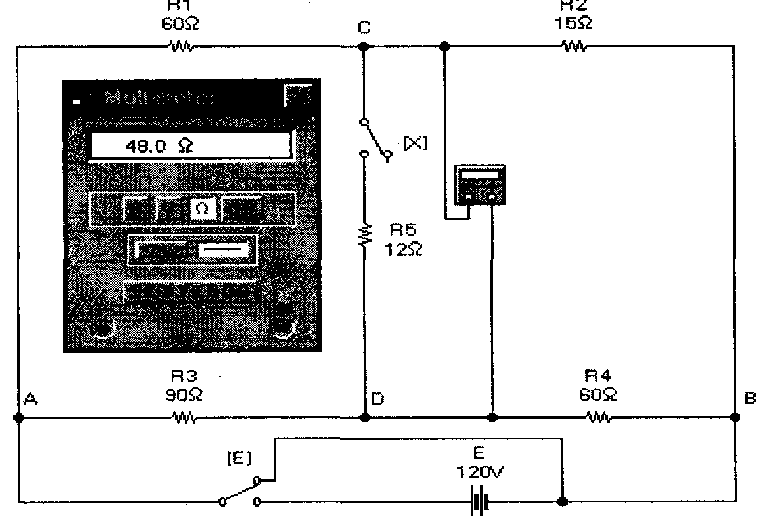
Рис. 8. Мостовая схема в режиме определения сопротивления короткого замыкания
2. Искомое сопротивление можно найти и другим путем. Для этого нужно замкнуть точки С и D накоротко, вычислить ток Iкз, протекающий через короткозамкнутый участок, и сопротивление короткого замыкания определить по формуле (6). Для моделирования такого режима необходимо ключ Е вернуть в исходное состояние, а мультиметр перевести в режим амперметра. Результаты моделирования показаны на рис. 9, из которого видно, что ток короткого замыкания равен 0,5 А. Тогда на основании формулы (6) Rкз=24/0,5=48 Ом.
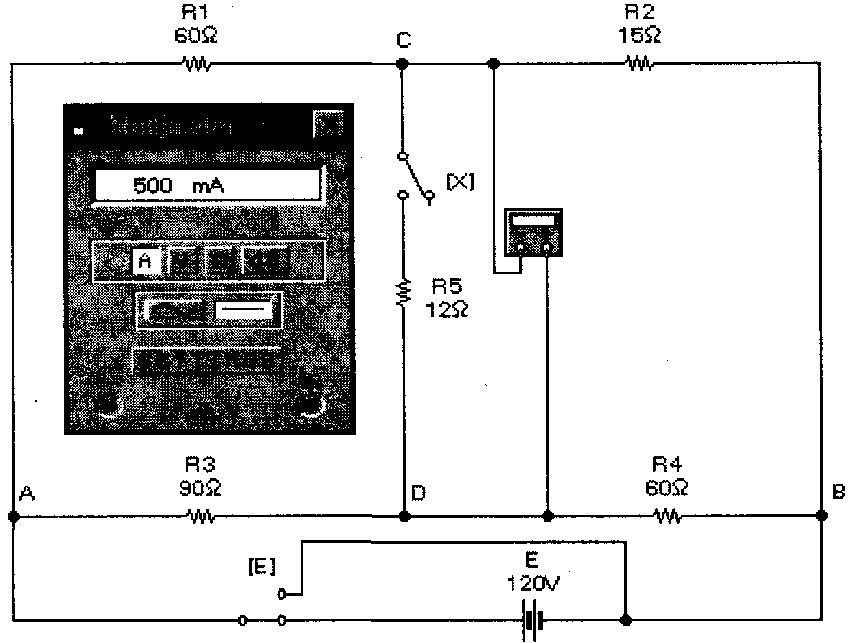
Рис. 9. Мостовая схема в режиме короткого замыкания исследуемой ветви
3. Теперь можно определить и искомый ток, используя формулу (7):
I5=Uхх/(R5+Rk)=24/(12+48)=0,4 A.
Для моделирования схемы в таком режиме ключ Х необходимо замкнуть, а мультиметр перевести в режим вольтметра. Результаты моделирования показаны на рис. 10 из которого видно, что падение напряжения на резисторе R5 равно 4,8 В, т.е. ток в цепи равен
4,8/12==0,4 А, что совпадает с расчетным значением.
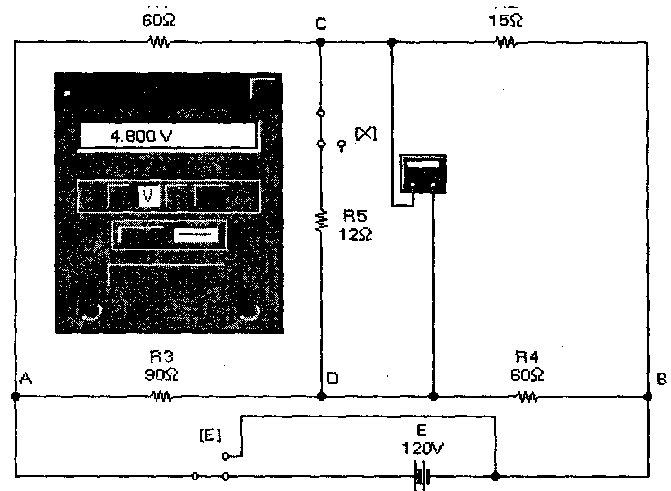
Рис. 10. Мостовая схема в рабочем состоянии
Кроме метода эквивалентного генератора напряжения, существует также и метод эквивалентного генератора тока. Его применение основано на взаимных преобразованиях источника тока и источника напряжения с использованием формул (1) и (2). Метод эквивалентного генератора тока на практике нашел ограниченное применение, поэтому рассматривать его не будем.
Индивидуальные задания
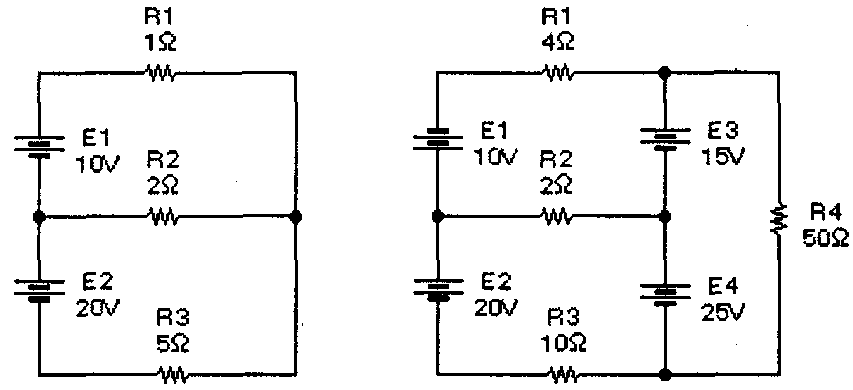
Рис 11. Двухконтурная (а) и трехконтурная (б) цепи постоянного тока
9. Поясните, в чем заключается метод наложения. Выполните расчет токов в ветвях схем на рис. (а) методом наложения и проверьте результаты расчета путем моделирования.
10. Какие законы теории цепей используются в методе эквивалентного генератора? Проведите расчеты и моделирование мостовой схемы (рис.7-10) во всех режимах при сопротивлении резистора R5=6 Ом.
1. Замена последовательных сопротивлений одним эквивалентным. Эквивалентное сопротивление R цепи, состоящей из последовательно соединенных сопротивлений R1, R2,…,.Rn, равно сумме этих сопротивлений:
R= R1+ R2+…+Rn(4)
2. Замена параллельных сопротивлений одним эквивалентным. Сопротивления параллельны, если все они присоединены к одной паре узлов. Эквивалентное сопротивление R цепи, состоящей из ряда параллельно соединенных сопротивлений, определяется из формулы суммирования проводимостей: l/R=l/ R1+l/ R2+...+l/ Rn (5)
В случае двух параллельно соединенных сопротивлений R=R1·R2/(R1+R2).
3. Преобразование треугольника сопротивлений (рис. 5, а) в эквивалентную звезду сопротивлений (рис. 5, б) и наоборот. Формулы преобразований имеют следующий вид:
R1=R12 R31/A; R2=R23 R12/A; R3=R31 R23/A;
R12=R1+R2+R1 R2/R3;
R23=R2+ R3+R2 R3/R1;
R31=R3+R1+R3 R1/R2,
где A=R12+R23+R13.

а) б)
Рис. 5. Включение сопротивлений треугольником (а) и звездой (б)
Вернемся к методу наложения и рассмотрим его применение для схемы на рис. 3.6. В этой схеме все источники напряжения идеальны, поэтому их внутренние сопротивления равны нулю. Предположим, что действует только ЭДС Е1, а вместо Е2 будет просто проводник (короткое замыкание). В этом случае ЭДС Е1 нагружена на эквивалентное сопротивление
R1экв=R2·R6/(R3+R6)+R4·R5/(R4+R5)=8 Ом.
При этом токи в ветвях составят:
I1'=E1/R1экв =96/8=12 A;
I3'=I1’·R6/(R3+R6)=12·6/9=8 A;
I4'=I1’·R5/(R4+R5)=12·10/25=4,8A;
I2'=I3’-I4'=8-4,8=3,2 A;
I6'=I1’-I3'=12-8=4 А;
I5'=I1’-14'=12-4.8=7,2 А.
Перейдем ко второму этапу, когда активной является ЭДС Е2, а Е1 — закорочена. В этом случае ЭДС Е2 нагружена на эквивалентное сопротивление R2экв=R3*R4/(R3+R4)+R5*R6/(
R5+R6)=6,25 Ом. При этом токи в ветвях имеют следующие значения;
I2"=E2/R2экв =75/2,5=12 A;
I3"=I2"·R4/(R3+R4)=12·15/18==10A;
I6"=I2"·R5/(R5+R6)=12·10/16=7,5A;
I1"=I3"-I6"=10- 7,5=2,5 А;
I4"=I2"-I3"=12-10==2 A;
I5"=I2"-I6"=12-7,5=4,5 A.
Складывая алгебраически токи, полученные от действия каждой ЭДС в отдельности, найдем истинные токи в каждой ветви:
I1=I1'-I1”=12+2,5=14,5 А;
I2=I2'+I2"=3,2+12=15,2 А;
I3=I3'+I3"=8+10=18 A;
I4=I4'-I4"=4,8-2=2,8A;
I5=I5'+I5"=7,2+4,5=11,7 A;
I6=I6"-I6'=7,5-4=2,5A,
что совпадает с результатами моделирования.

Рис. 6. Схема многоконтурной цепи
Метод эквивалентного генератора
Метод эквивалентного генератора напряжения называют иногда методом короткого замыкания и холостого хода или методом активного двухполюсника. С его помощью определяется ток в определенной ветви схемы. Назовем ее АВ и предположим, что она содержит одно сопротивление R. Для нахождения тока в этой ветви размыкают ветвь и любым из рассмотренных выше методов определяют разность потенциалов Uxx на зажимах А, В разомкнутой ветви (режим холостого хода). Затем вычисляется сопротивление короткого замыкания Rкз равное эквивалентному сопротивлению остальной цепи. При этом имеющиеся в схеме источники должны быть выключены и заменены их внутренними сопротивлениями, а питание схемы осуществляется от постороннего источника, подключенного к зажимам А, В исследуемой ветви. Следующим этапом является режим короткого замыкания, при котором определяется ток Iкз в ветви АВ при закороченных зажимах А, В. Заметим, что этот этап не обязателен, если сопротивление Rкз удалось определить другим, более простым способом. Если же режим короткого замыкания все-таки пришлось применить, то в этом случае
Rкз = Uxx / Iкз (6)
и искомый ток в ветви определяется из выражения:
I= Uxx /(R+ Rкз) (7)
Перейдем к конкретному примеру. Для этого воспользуемся схемой на рис. 7, которая представляет собой мостовую схему из двух плеч, образованных резисторами Rl, R2, RЗ, R4. В одну диагональ моста включен идеальный источник напряжения Е и переключатель, управляемый клавишей Е клавиатуры.

Рис. 7. Мостовая схема в режиме холостого хода
В другую диагональ моста включен резистор R5 с ключом X, который управляется одноименной клавишей. Нашей задачей является определение тока через резистор R5 в рабочем состоянии, когда ключ Х замкнут. В положении ключа X, показанном на схеме (ключ разомкнут), реализуется первый этап моделирования — режим холостого хода ветви CD. В этом режиме через сопротивления Rl, R2 протекает ток I', а через сопротивления R3, R4 — ток I", которые равны соответственно I’=E/(Rl
+R2)=120/75=l,6A;
I”=E/(R3+R4)=120/150=0,8A.
При этом потенциалы в точках С и D определяются падениями напряжений на резисторах Rl и R3: Uac=I’Rl=l,6*60=96B;
Uad=I''RЗ=0,8 *90=72 В.
Располагая потенциалами точек С и D, нетрудно найти и напряжение между ними, которое равно напряжению холостого хода:
Ucd = Uxx = Uac - Uad =96-72=24 В,
что соответствует показаниям мультиметра на рис. 7.
Теперь найдем сопротивление короткого замыкания. Как отмечалось выше, сделать это можно двумя способами.
1. Путем непосредственного расчета с использованием данных схемы. В этом случае источник Е нужно выключить, оставив его внутреннее сопротивление, равное в данном случае нулю. Сопротивление короткого замыкания будет равно сопротивлению цепи между точками С и D:
Rкз=R1*R2/(R1+R2)+R3*R4/(R3+R4).
При моделировании на схеме рис. 7 необходимо ключ Е перевести в другое положение, а мультиметр — в режим омметра. Результаты таких действий показаны на рис. 8, откуда видно, что результаты проведенного расчета полностью подтверждаются результатами моделирования.

Рис. 8. Мостовая схема в режиме определения сопротивления короткого замыкания
2. Искомое сопротивление можно найти и другим путем. Для этого нужно замкнуть точки С и D накоротко, вычислить ток Iкз, протекающий через короткозамкнутый участок, и сопротивление короткого замыкания определить по формуле (6). Для моделирования такого режима необходимо ключ Е вернуть в исходное состояние, а мультиметр перевести в режим амперметра. Результаты моделирования показаны на рис. 9, из которого видно, что ток короткого замыкания равен 0,5 А. Тогда на основании формулы (6) Rкз=24/0,5=48 Ом.

Рис. 9. Мостовая схема в режиме короткого замыкания исследуемой ветви
3. Теперь можно определить и искомый ток, используя формулу (7):
I5=Uхх/(R5+Rk)=24/(12+48)=0,4 A.
Для моделирования схемы в таком режиме ключ Х необходимо замкнуть, а мультиметр перевести в режим вольтметра. Результаты моделирования показаны на рис. 10 из которого видно, что падение напряжения на резисторе R5 равно 4,8 В, т.е. ток в цепи равен
4,8/12==0,4 А, что совпадает с расчетным значением.

Рис. 10. Мостовая схема в рабочем состоянии
Кроме метода эквивалентного генератора напряжения, существует также и метод эквивалентного генератора тока. Его применение основано на взаимных преобразованиях источника тока и источника напряжения с использованием формул (1) и (2). Метод эквивалентного генератора тока на практике нашел ограниченное применение, поэтому рассматривать его не будем.
Индивидуальные задания
-
Что представляет собой режим холостого хода и режим короткого замыкания? Для схемы на рис. 1 проведите моделирование режимов холостого хода и короткого замыкания и сравните полученные результаты с расчетными. -
Сформулируйте закон Ома для участка цепи. Чем он отличается от закона Ома для полной цепи? Проведите моделирование схемы на рис. 2, уменьшив ЭДС источников Е1 и Е2 в 4 раза. -
Сформулируйте первый и второй законы Кирхгофа. Проведите расчеты по определению токов в ветвях с использованием законов Кирхгофа для цепи (рис.11 а). После подключения к схеме необходимых измерительных приборов проведите её моделирование. Сравните полученные данные с результатами расчетов. -
Сформулируйте законы Кирхгофа. Используя законы Кирхгофа, проведите расчеты по определению токов в ветвях для цепи на рис. 11 б. После подключения к схеме необходимых измерительных приборов проведите её моделирование. Сравните полученные данные с результатами расчетов.

Рис 11. Двухконтурная (а) и трехконтурная (б) цепи постоянного тока
-
В чем заключается отличие метода контурных токов от метода расчета с использованием законов Кирхгофа для аналогичных целей? Выполните расчет токов в ветвях схемы на рис. 4 методом контурных токов при Е1=50 В, Е2==15 В, Е3=5 В и Е4==3 В. Сравните полученные данные с результатами моделирования. -
Какие законы используются при расчете токов ветвей методом наложения? Выполните расчет токов в ветвях схемы на рис. 5. методом наложения при Е1=48 В и Е2=45 В. Сравните полученные данные с результатами моделирования.
9. Поясните, в чем заключается метод наложения. Выполните расчет токов в ветвях схем на рис. (а) методом наложения и проверьте результаты расчета путем моделирования.
10. Какие законы теории цепей используются в методе эквивалентного генератора? Проведите расчеты и моделирование мостовой схемы (рис.7-10) во всех режимах при сопротивлении резистора R5=6 Ом.