Моделирование и расчет электрических цепей в виртуальной электронной лаборатории

Реальные источники электрической энергии можно представить двояко:

1) в виде генератора напряжения, который характеризуется ЭДС Е, численно равной напряжению холостого хода и включенной последовательно с внутренним сопротивлением Ri;

2) в виде генератора тока, который характеризуется током I, численно равным току короткого замыкания реального источника, и параллельно подключенной проводимостью Gi.

Переход от генератора напряжения к эквивалентному генератору тока осуществляется по формулам:

I=E/Ri, Gi= 1/Ri, (1)

а обратный переход от генератора тока к эквивалентному генератору напряжения по формулам:

E=I/Gi, Ri=l/Gi (2)

У идеального генератора напряжения внутреннее сопротивление Ri равно нулю, а у идеального генератора тока равна нулю внутренняя проводимость Gi.

Закон Ома

З-н Ома для участка цепи: ток в проводнике I равен отношению падения напряжения U на участке цепи к ее электрическому сопротивлению R:

I=U/R (3)



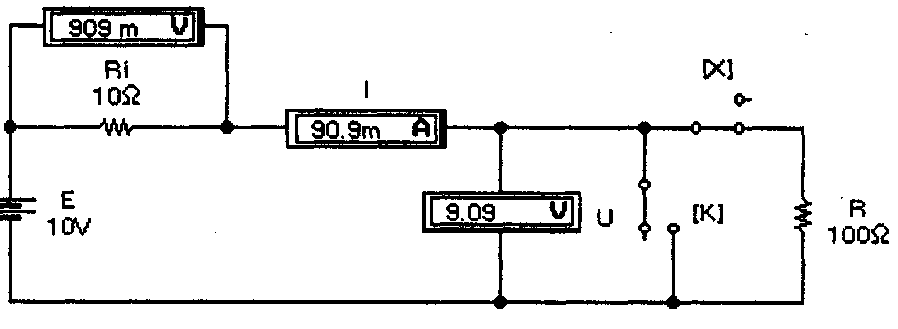
Рис. 1. Простейшая цепь постоянного тока

Закон Ома иллюстрируется схемой на рис. 1, из которой видно, что на участке цепи с сопротивлением R=100 Ом создается падение напряжения U=9,09В, измеряемое вольтметром. Согласно (3) ток в цепи I=9,09/100=90,9 мА, что и измеряет последовательно включенный в цепь амперметр. Отметим, что в рассматриваемой схеме внутреннее сопротивление амперметра выбрано равным 10¹² Ом, т.е. очень малым, а входное сопротивление вольтметра -10¹² Ом, т.е. очень большим, чтобы подключение измерительных приборов к цепи не оказывало сколько-нибудь заметного влияния на результаты измерений.

Отметим назначение ключей К и Х на рис. 1, управляемых нажатием одноименных клавиш клавиатуры. При размыкании ключа Х в схеме реализуется режим холостого хода, при этом вольтметр U измеряет ЭДС источника Е=10 В, а вольтметр Ui имеет нулевые показания. При замыкании ключа К в схеме реализуется режим короткого замыкания и, согласно (1), ток короткого замыкания Io=E/Ri=l0/10=l А. При этом вольтметр Ui измеряет падение напряжения Ui=Io·Ri=10 В.

---

З-н Ома для полной цепи: ток в замкнутой электрической цепи равен ЭДС источника Е, деленной на сопротивление всей цепи. Применительно к цепи на рис. 1 ее полное сопротивление равно Ri + R, и на основании закона Ома получаем I=E/(Ri+R)=90,9 мА, что и измеряет амперметр.

Отметим, что на дисплее амперметра отображаются только три старшие разряда измеряемой величины, так что результат измерения округляется.

Обобщенный з-н Ома: ток в замкнутой одноконтурной цепи равен отношению алгебраической суммы всех ЭДС к арифметической сумме всех сопротивлений. Перед расчетом выбирают направление обхода контура и считают это направление за положительное направление тока. При определении алгебраической суммы ЭДС со знаком плюс берут те ЭДС, направления которых совпадают с выбранным положительным направлением тока, и со знаком минус — ЭДС с противоположными направлениями.

В качестве примера рассмотрим одноконтурную цепь (рис. 2), состоящую из источников напряжения Е1=120 В, Е2=40 В и резисторов с сопротивлениями Rl=12 Ом и R2=8 Ом. Определим напряжение между точками А и В.



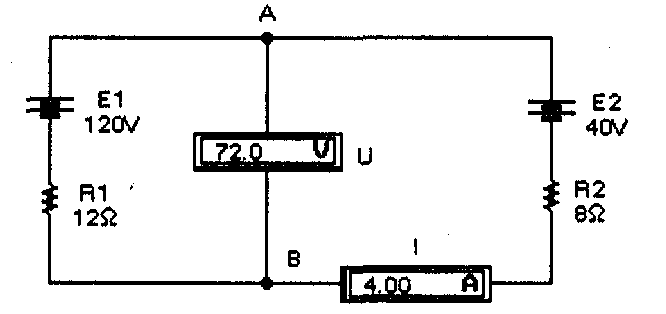
Рис. 2. Одноконтурная цепь с двумя источниками напряжения

Выберем направление обхода контура по часовой стрелке. В таком случае ЭДС Е1 войдет со знаком "+", поскольку ток от Е1 совпадает с направлением обхода (положительным направлением тока во внешней цепи считается направление от поло­жительного к отрицательному зажиму источника). При обходе же ветви с источником Е2 направление обхода не совпадает с направлением тока, который создается этим источником.

Поэтому для схемы на рис. 2 ток в цепи I=(Е1-E2)/(R1+R2)=80/20=4А.

Так как величина тока получилась положительной, то, следовательно, направление тока совпадает с выбранным. Если бы результат полу­чился отрицательным, то это означает, что действительное направление тока в цепи противоположно выбранному.

Напряжение U_ab между точками А и В определяется с помощью закона Ома для участка цепи. Выберем участок А-Е2-В. Для этого участка закон Ома запишется в следующем виде:

I=(Uab-E2)/R2, откуда Uab=E2+I·R2=40+4·8=72 В.

Законы Кирхгофа

Первый закон Кирхгофа: алгебраическая сумма всех токов, втекающих в любой узел

---

, равна нулю. Токи, втекающие в узел, условно принимаются положительными, а вытекающие из него — отрицательными (или наоборот). Если, например, в узел втекает ток I1, а вытекают токиI2 и I3, то первый закон Кирхгофа может быть записан в виде выражения: I1-I2-I3=0.

Второй закон Кирхгофа: алгебраическая сумма ЭДС любого замкнутого кон­тура равна алгебраической сумме падений напряжений на всех участках контура.

При применении второго закона Кирхгофа необходимо учитывать знаки ЭДС и выбранное направление токов на всех участках контура. Направление обхода контура выбирается произвольным; при записи левой части равенства ЭДС, направле­ния которых совпадают с выбранным направлением обхода независимо от направления протекающего через них тока, принимаются положительными, а ЭДС обратного направления принимаются отрицательными. При записи правой части равенства со знаком плюс берутся падения напряжения на тех участках, в которых положительное направление тока совпадает с направлением обхода независимо от направления ЭДС на этих участках, и со знаком минус — на участках, в которых положительное направление тока противоположно направлению обхода.

Общая методика применения законов Кирхгофа для расчета сложных много­контурных цепей такова. Устанавливается число неизвестных токов, которое равно числу ветвей р. Для каждой ветви задается положительное направление тока. Число независимых уравнений, составляемых по первому закону Кирхгофа, равно числу узлов q (точек соединения не менее чем трех проводников) минус единица, т.е. q-1. Число независимых уравнений, составляемых по второму закону Кирхгофа, равно числу контуров n=p-q+1. Общее число уравнений, составляемых по первому и второму законам Кирхгофа, равно числу неизвестных токов р. Решение этой системы уравнений и дает значения искомых токов.

Для иллюстрации изложенной методики рассмотрим многоконтурную цепь постоянного тока на рис. 3. В этой цепи всего три узла: А, В и С (q=3), следовательно, число независимых уравнений, составляемых по первому закону Кирхгофа, будет на единицу меньше, т.е. два. При числе ветвей цепи р=5 число контуров n=5-З+1=З, следовательно, по второму закону Кирхгофа можно составить три взаимно

---

независимых уравнения. Таким образом, общее число независимых уравнений, составляемых по первому и второму законам Кирхгофа, будет равно числу неизвестных токов в пяти ветвях схемы.



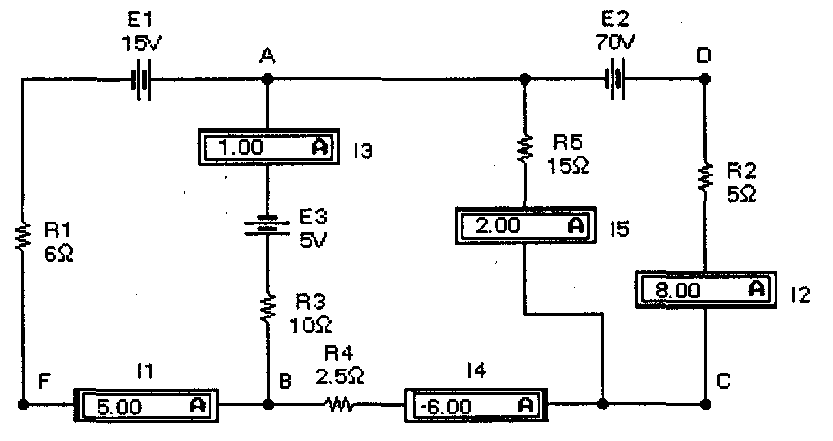
Рис. 3. Многоконтурная цепь постоянного тока

Выберем положительные направления токов, которые на схеме обозначены соответствующим включением амперметров. Например, ток I1 течет справа налево и втекает в узел А (положительное направление тока), поскольку отрицательная лемма, отмеченная утолщенной черной линией, находится слева и ток через амперметр будет течь справа налево. Ток I2 вытекает из узла А, поскольку ток через одноименный амперметр будет течь сверху вниз (к отрицательному зажиму, расположенному на нижней грани иконки) и т.д.

Составим систему уравнений Кирхгофа:

для уза A	I1-I2+I3-I5=0
для узла B	-I1-I3-I14=0
для контура ABFA	E1+E2=I1-R1-I3-R3
для контура ABCA	E3=-I3-R3+I4-R4+I5-R5
ля контура ADCA	E2=I2-R2+I5-R5

После подстановки в полученные уравнения числовых значений они приобретают следующий вид:

I1-I2+I3-I5=0 I1-I3-I4=0 6-I1-10·I3=20 -10-I3+2,5·I4+15·I5=5 5·I2+15·I5=70

Решив полученную систему уравнений, имеем: I1=5А; I2=8А; I3=1А; I4= -6А; I5=2А, что соответствует показаниям приборов. Отрицательный знак для тока I4 означает, что истинное направление этого тока противоположно принятому.

Метод контурных токов

Метод контурных токов (метод Максвелла) напоминает метод расчета с использованием законов Кирхгофа, однако он несколько проще и поэтому получил большее распространение на практике при расчетах многоконтурных цепей, состоящих из n независимых контуров. Определение токов в ветвях сводится к решению системы n=p-q+1 уравнений для контурных токов I_1k, I_2k,I_3k …; действительный же ток в каждой ветви находится как алгебраическая сумма контурных токов, протека­ющих через соответствующую ветвь. Выбор направлений контурных токов произволен. Каждая из ветвей сложной электрической цепи должна войти хотя бы в один из анализируемых контуров.

---

Для иллюстрации рассматриваемого метода расчета обратимся к схеме на рис.4, на которой выбранные направления контурных токов обозначены стрелками, токи в ветвях контуров — расположением входных зажимов амперметров.

Составим систему уравнений для контуров:

El-E2-E3= I1k (Rl+R2)- I2k R2

E2-E4= I2k (R2+R5+R4)- I3k R4- I1k R2

-E3-E4= I3k (R6+R4)+ I2kR4

После подстановки числовых значений получим:

60=20 I1k –10 I2k

24= -10 I1k +22 I2k +7 I3k

-16=7 I2k +22 I3k

Решив эту систему уравнений, найдем контурные токи:

I1k = 5 А, I2k = 4 A, I3k= -2 А.

Теперь найдем истинные токи во всех ветвях. В ветви, где действует ЭДС Е1, истинный ток I1 имеет направление контурного тока I1k и равен ему: I1= I1k= 5А. В ветви с сопротивлением R5 истинный ток I5 имеет направление контурного тока I2kи равен ему: I5 = I2k = 4А. В ветви с сопротивлением R6 истинный ток I6 имеет направление, противоположное контурному току I_3k, и равен I6= - I3k = 2 А. В ветви с сопротивлением R2 истинный ток I2 получится наложением контурных токов I1kи I2k и будет иметь направление большего из них, т.е. I2= I1k - I2k =1А. В ветви с сопротивлением R4 истинный токI4 получится наложением контурных токов I2kи I3kи будет иметь направление большего из них, т.е. I4= I2k + I3k =4+(-2)=2 А. В ветви, где действу­ет ЭДС ЕЗ, истинный ток I3 получится наложением контурных токов I1k и I3k и будет иметь направление тока I1k, т.е. I3= I1k + I3k =5+(-2)=3А. Из сравнения полученных расчетных данных с показаниями приборов на рис. 4 видно, что они полностью совпадают.

.

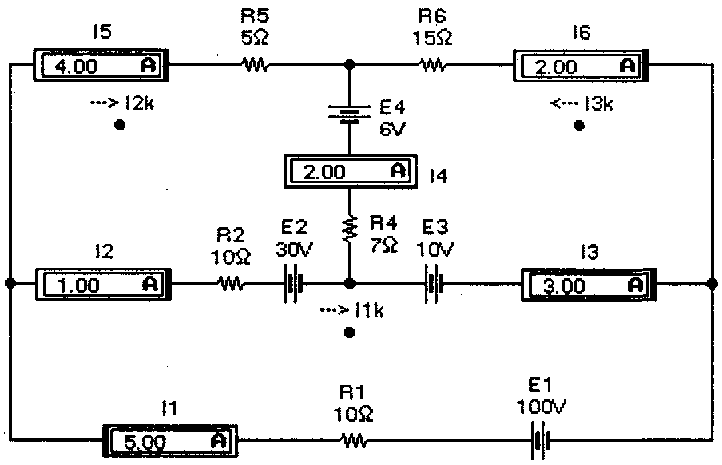
Рис. 4. Схема сложной трехконтурной цепи

Метод наложения

При методе наложения ток в любой ветви схемы рассчитывается как алгебраическая сумма токов, вызываемых в ней каждой ЭДС в отдельности. При этом предполагается, что при анализе воздействия одной ЭДС остальные ЭДС принимаются равными нулю и при расчетах учитываются только их внутренние сопротивления.

При использовании метода наложения потребуются некоторые навыки в преобразовании электрических цепей. Во всех случаях замена одних схем другими, им эквивалентными, не должна приводить к изменению

---

Смотрите также файлы

• Дисциплина Философия.docx

• Описание технологического процесса.docx

• Экономические ресурсы и их виды.docx

• Расчет ректификационной колонны для Разделения бинарной смеси по мдк.docx

• Конкуренция процессного и проектного подхода в качестве инструментов стратегического управления.docx