Файл: Северокавказская государственная гуманитарнотехнологическая академия.doc
Добавлен: 22.11.2023
Просмотров: 123
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
i. Существует несколько способов решения этой задачи.
Уточнение коэффициентов аналитической зависимости y=f(x,a,b) производится тремя методами: методом выбранных точек; методом средних; методом наименьших квадратов.
Определение параметров эмпирической зависимости по методу выбранных точек
По экспериментальным значениям, преобразованным по методу выравнивания, на координатной плоскости наносится система точек. Затем проводится простейшая плавная линия, которая наиболее близко примыкает к данным точкам. На этой линии выбираются точки, которые не принадлежат исходной системе точек. Они должны быть равномерно распределены, а их число должно быть равно количеству искомых параметров эмпирической зависимости. Координаты этих точек (xj,yj) тщательно измеряются и используются для записи условия прохождения графика эмпирической функции (1) через выбранные точки
xj,ao,a1,...,am) = yj , j = 0,1,...,m (2)
Из этой системы уравнений находим значения параметров ao,a1,...,am.
В частности, если в качестве эмпирической формулы принята линейная зависимость y = ax + b, то на этой прямой выбираются две точки (по количеству неизвестных параметров эмпирической зависимости) с координатами (x1,y1) и (x2,y2).
Уравнения (2) примут вид системы:
ax1 + b = y1
ax2 + b = y2
решая которую, находим коэффициенты a и b.
С целью определения отклонений нужно составить следующую таблицу:
Определение параметров эмпирической зависимости по методу средних
Метод состоит в том, что параметры ao, a1,..., am зависимости (1) определяются с использованием условия равенства нулю суммы отклонений во всех точках xi:
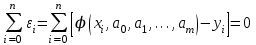 (3)
(3)
Полученное уравнение служит для определения параметров а0,a1,...,am. Ясно, что из одного уравнения нельзя однозначно определить все m+1 параметров. Однако, поскольку других условий нет, равенство (3), путем группировки отклонений i разбивается на систему, состоящую из m+1 уравнений. Например,
Решая эту систему уравнений, можно найти неизвестные параметры.
В процессе группировки необходимо все отклонения располагать по возрастанию номеров. В каждом уравнении должно быть примерно одинаковое количество отклонений.
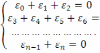
С целью определения отклонений нужно составить следующую таблицу:
Рассмотренные методы определения параметров эмпирической зависимости (метод выбранных точек и метод средних) являются сравнительно простыми, однако в ряде случаев получаемые с их помощью аппроксимации не обладают достаточной точностью.
Определение параметров эмпирической зависимости по методу наименьших квадратов
Запишем сумму квадратов отклонений для всех точек xo,x1,...,xn
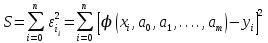
Параметры ao,a1,...,am эмпирической формулы (1) будем находить из условия минимума функции
S = S( ao,a1,...,am )
В этом состоит метод наименьших квадратов.
С целью упрощения расчетов согласно данному методу рекомендуется составить таблицу, где n - количество значений переменной х:
По итогам таблицы составляется система уравнений
∑ x0· а + ∑ x1· b = ∑ y
∑ x1· а + ∑ x2· b = ∑ x · y
решив которую, можно определить наилучшие значения параметров a и b.
Естественно ожидать, что значения найденной функции y=f(x,a,b)в точках х1, х2,...,хn будут отличаться от табличных значений y1, y2,...,yn. Для определения имеющихся отклонений необходимо составить таблицу (см. таблица метода выбранных точек). В соответствии с методом наименьших квадратов сумма квадратов полученных отклонений для заданного вида приближающей функции (и найденных значений параметров a и b) должна быть наименьшей
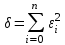 (5)
(5)
Из двух разных приближений одной и той же табличной функции, следуя принципу наименьших квадратов, лучшим нужно считать то, для которого сумма (5) имеет наименьшее значение.
Индивидуальные задания к расчетно-графической работе
Подобрать эмпирическую зависимость и определить ее параметры различными методами: 1) методом выбранных точек; 2) методом средних;
3) методом наименьших квадратов.
Сравнить точность аппроксимации экспериментальных данных, используя вышеназванные методы с помощью следующей таблицы:










N X Y Y1 Y2 Y3 1 2 3
1 ... ... ... ... ... ... ... ...
2 ... ... ... ... ... ... ... ...
Экспериментальные данные для различных вариантов:
Уточнение коэффициентов аналитической зависимости y=f(x,a,b) производится тремя методами: методом выбранных точек; методом средних; методом наименьших квадратов.
Определение параметров эмпирической зависимости по методу выбранных точек
По экспериментальным значениям, преобразованным по методу выравнивания, на координатной плоскости наносится система точек. Затем проводится простейшая плавная линия, которая наиболее близко примыкает к данным точкам. На этой линии выбираются точки, которые не принадлежат исходной системе точек. Они должны быть равномерно распределены, а их число должно быть равно количеству искомых параметров эмпирической зависимости. Координаты этих точек (xj,yj) тщательно измеряются и используются для записи условия прохождения графика эмпирической функции (1) через выбранные точки
xj,ao,a1,...,am) = yj , j = 0,1,...,m (2)
Из этой системы уравнений находим значения параметров ao,a1,...,am.
В частности, если в качестве эмпирической формулы принята линейная зависимость y = ax + b, то на этой прямой выбираются две точки (по количеству неизвестных параметров эмпирической зависимости) с координатами (x1,y1) и (x2,y2).
Уравнения (2) примут вид системы:
ax1 + b = y1
ax2 + b = y2
решая которую, находим коэффициенты a и b.
С целью определения отклонений нужно составить следующую таблицу:
| X | | | | | | |
| Y | | | | | | |
| Y*=aX+b | | | | | | |
| ε = |Y-Y*| | | | | | | |
Определение параметров эмпирической зависимости по методу средних
Метод состоит в том, что параметры ao, a1,..., am зависимости (1) определяются с использованием условия равенства нулю суммы отклонений во всех точках xi:
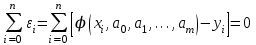 (3)
(3)Полученное уравнение служит для определения параметров а0,a1,...,am. Ясно, что из одного уравнения нельзя однозначно определить все m+1 параметров. Однако, поскольку других условий нет, равенство (3), путем группировки отклонений i разбивается на систему, состоящую из m+1 уравнений. Например,
Решая эту систему уравнений, можно найти неизвестные параметры.
В процессе группировки необходимо все отклонения располагать по возрастанию номеров. В каждом уравнении должно быть примерно одинаковое количество отклонений.
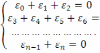
С целью определения отклонений нужно составить следующую таблицу:
| X | | | | | | |
| Y | | | | | | |
| Y*=aX+b | | | | | | |
| ε = |Y-Y*| | | | | | | |
Рассмотренные методы определения параметров эмпирической зависимости (метод выбранных точек и метод средних) являются сравнительно простыми, однако в ряде случаев получаемые с их помощью аппроксимации не обладают достаточной точностью.
Определение параметров эмпирической зависимости по методу наименьших квадратов
Запишем сумму квадратов отклонений для всех точек xo,x1,...,xn
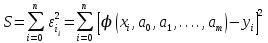
Параметры ao,a1,...,am эмпирической формулы (1) будем находить из условия минимума функции
S = S( ao,a1,...,am )
В этом состоит метод наименьших квадратов.
С целью упрощения расчетов согласно данному методу рекомендуется составить таблицу, где n - количество значений переменной х:
| x0 | x1 | x2 | y | x · y |
| 1 . . . 1 | x 1 x 2 . . x n | . . . . . | y 1 y 2 . . y n | . . . . . |
| ∑ x0 | ∑ x1 | ∑ x2 | ∑ y | ∑ x · y |
По итогам таблицы составляется система уравнений
∑ x0· а + ∑ x1· b = ∑ y
∑ x1· а + ∑ x2· b = ∑ x · y
решив которую, можно определить наилучшие значения параметров a и b.
Естественно ожидать, что значения найденной функции y=f(x,a,b)в точках х1, х2,...,хn будут отличаться от табличных значений y1, y2,...,yn. Для определения имеющихся отклонений необходимо составить таблицу (см. таблица метода выбранных точек). В соответствии с методом наименьших квадратов сумма квадратов полученных отклонений для заданного вида приближающей функции (и найденных значений параметров a и b) должна быть наименьшей
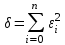 (5)
(5)Из двух разных приближений одной и той же табличной функции, следуя принципу наименьших квадратов, лучшим нужно считать то, для которого сумма (5) имеет наименьшее значение.
Индивидуальные задания к расчетно-графической работе
Подобрать эмпирическую зависимость и определить ее параметры различными методами: 1) методом выбранных точек; 2) методом средних;
3) методом наименьших квадратов.
Сравнить точность аппроксимации экспериментальных данных, используя вышеназванные методы с помощью следующей таблицы:










N X Y Y1 Y2 Y3 1 2 3
1 ... ... ... ... ... ... ... ...
2 ... ... ... ... ... ... ... ...
Экспериментальные данные для различных вариантов:
| № Вар. | Данные эксперимента | |||||||||
| 1 | Х | 500 | 750 | 1000 | 1250 | 1500 | | | | |
| Y | 3,23 | 4,52 | 5,71 | 10,17 | 18,49 | | | | | |
| 2 | Х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | 0,33 | 0,49 | 0,59 | 0,65 | 0,71 | 0,755 | 0,77 | 0,81 | 0,82 | |
| 3 | Х | 1 | 2 | 3 | 4 | | | | | |
| Y | 623 | 676 | 746 | 829 | | | | | | |
| 4 | Х | 10 | 20 | 30 | 40 | 50 | | | | |
| Y | 271,7 | 287,6 | 296,9 | 303,5 | 308,6 | | | | | |
| 5 | Х | 55 | 60 | 65 | 70 | | | | | |
| Y | 6 | 11,3 | 22,6 | 36 | | | | | | |
| 6 | Х | 7 | 12 | 17 | 21 | 28 | | | | |
| Y | 0,24 | 0,2 | 0,19 | 0,18 | 0,178 | | | | | |
| 7 | Х | 11 | 12 | 13 | 14 | 15 | | | | |
| Y | 76,16 | 89,85 | 104,6 | 120,4 | 137,3 | | | | | |
| 8 | Х | 65 | 66 | 67 | 68 | 69 | 70 | 71 | | |
| Y | 10,1 | 15,1 | 19,7 | 25,3 | 31,5 | 37,6 | 42,7 | | | |
| 9 | Х | 1 | 2 | 3 | 4 | 5 | 6 | | | |
| Y | 104 | 113 | 119 | 122 | 130 | 137 | | | | |
| 10 | Х | 1 | 2 | 3 | 4 | 5 | 6 | | | |
| Y | 18 | 19 | 21 | 22 | 23 | 25 | | | | |
| 11 | Х | 1 | 2 | 3 | 4 | 5 | 6 | | | |
| Y | 61 | 66 | 71,2 | 79,6 | 82 | 87,7 | | | | |
| 12 | Х | 65 | 66 | 67 | 69 | 69 | 70 | | | |
| Y | 124,1 | 127,8 | 127,7 | 142,3 | 143,6 | 146,8 | | | | |
| 13 | Х | 2,5 | 7 | 11,8 | 14 | 16 | | | | |
| Y | 1,9 | 5,1 | 8,66 | 9,83 | 10,73 | | | | | |
| 14 | Х | 10 | 12 | 14 | 16 | 18 | 20 | | | |
| Y | 23 | 24,2 | 27,6 | 30 | 28,7 | 37 | | | | |
| 15 | Х | 65 | 66 | 67 | 68 | 69 | 70 | | | |
| Y | 38,1 | 45,1 | 53,5 | 62,1 | 71,5 | 78,2 | | | | |
| 16 | Х | 65 | 66 | 67 | 68 | 69 | | | | |
| Y | 335 | 350 | 350 | 383 | 400 | | | | | |
| 17 | Х | 40 | 50 | 60 | 70 | | | | | |
| Y | 13,2 | 19,2 | 29,3 | 45,8 | | | | | | |
| 18 | Х | 50 | 60 | 65 | 70 | | | | | |
| Y | 101 | 106 | 126 | 142 | | | | | | |
| 19 | Х | 1 | 3 | 7 | 8 | 11 | | | | |
| Y | 21 | 87 | 370 | 492 | 1344 | | | | | |
| 20 | Х | 19 | 26 | 29 | 51 | | | | | |
| Y | 10,88 | 12,18 | 12,67 | 15,5 | | | | | | |
| 21 | Х | 11 | 15 | 19 | 24 | | | | | |
| Y | 2,7 | 3,1 | 3,34 | 3,56 | | | | | | |
| 22 | Х | 2 | 5 | 7 | 9 | | | | | |
| Y | 1,23 | 2,1 | 2,4 | 2,67 | | | | | | |
| 23 | Х | 2 | 3 | 5 | 6 | 8 | | | | |
| Y | 9 | 23 | 157 | 408 | 2756 | | | | | |
| 24 | Х | 2 | 3 | 4 | 5 | | | | | |
| Y | -41 | -87 | -205 | -315 | | | | | | |
| 25 | Х | 3 | 4 | 5 | 6 | 7 | | | | |
| Y | 0,29 | 0,38 | 0,46 | 0,54 | 0,62 | | | | | |
| 26 | Х | 2 | 4 | 5 | 7 | | | | | |
| Y | 14 | 268 | 699 | 2970 | | | | | | |
| 27 | Х | 11 | 14 | 17 | 21 | 24 | | | | |
| Y | 6,6 | 5,3 | 4,3 | 3,2 | 2,6 | | | | | |
| 28 | Х | 2 | 6 | 8 | 10 | | | | | |
| Y | 1,65 | 5,5 | 6 | 6,4 | | | | | | |
| 29 | Х | 8 | 12 | 14 | 17 | | | | | |
| Y | 32,3 | 26,1 | 19,9 | 22,2 | | | | | | |