Файл: Методическое пособие. Москва. Издательский центр ВентанаГраф.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 68
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольные работы по алгебре 7 класс (углубленное изучение) к учебнику
А.Г.Мерзляк »Алгебра 7 класс».
Методический комплект:Алгебра 7.Самостоятельные и контрольные работы. Москва.Издательский центр «Вентана-Граф» 2017г.2.Алгебра 7. Методическое пособие. Москва. Издательский центр «Вентана-Граф».2015г.
| Отметка | «Контрольная работа» | «4» | «5» |
| Обязательная часть | 5 заданий | 6 заданий | 6 заданий |
| Дополнительная часть | | 1 задание | 2 задания |
Контрольная работа № 1 по теме «Линейное уравнение с одной переменной»
Вариант 1.
1.Решите уравнение. 1).(2x-3)(3x+6)(2?8-0,4x)=0 ; 2)
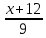 –
–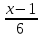 =
=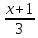
3.Первой бригаде надо было отремонтировать 180 м. дроги, а второй-160 м. Первая бригада отремонтировала ежедневно 40 м. , вторая -25м..Через сколько дней первой бригаде останется отремонтировать в 3 раза меньше дороги ,чем второй ?.
4)Решите уравнение: 1). | 3x-6|-2=10; 2).| |x| +5|=6; 3). |x+4|=|x-7|.
4.Лодка плыла 2,4ч. по течению реки и 0,8 ч. против течения. При этом путь ,пройденный против течения реки на 19,2 км. Больше, чем путь, пройденный против течения. Найдите собственную скорость лодки, если скорость течения реки равна 3 км/ч.
5. Найдите все целые значения a , при которых корень уравнения ax=-8 является натуральным числом.
6. Каким выражением можно заменить звездочку в равенстве 2x-8=4x+* , чтобы получилось уравнение:
1) не имеющее корней; 2) имеющее бесконечно много корней;
3) имеющее один корень?
Вариант 2
1.Решите уравнение: 1).(5x+30)(4x-6)(4,8-0,8)=0 ; 2)
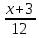 –
–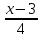 =
=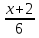
2.В первом контейнере было 200 кг. Яблок, а во втором-120 кг. Из первого контейнера брали ежедневно по 30 кг. Яблок, а из второго –по 25 кг. Через сколько дней в первом контейнере останется в 4 раза больше яблок ,чем во втором?
3.Решите уравнение: 1).|4x+8| + 3=11 ; 2). ||x|+7|=8; 3).|x+5| = |x-4|.
4. Лодка плыла 2,8 ч. по течению реки и 1,6 ч. против течения. При этом путь, пройденный лодкой по течению реки, на 36,8 км. Больше, чем путь, пройденный против течения. Найдите собственную скорость лодки, если скорость течения реки равна 4 км/ч.
5. Найдите все целые значения a , при которых корень уравнения ax=-6 является натуральным числом.
6. Каким выражением можно заменить звездочку в равенстве 4x+3=6x+*, чтобы получилось уравнение:
1) не имеющее корней; 2) имеющее бесконечно много корней;3) имеющее один корень.
Контрольная работа №2 по теме « Целые выражения»
Вариант 1.
1.Вычислите:(3⁴ ꞉ 10-0,1³ ·100): 0,4² .
2.Представьте в виде степени с основанием x выражение:
1). (x⁵)²· (x² ·x )⁴ ; 2).
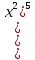 ·
·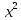 ; 3)
; 3) )⁴ ·
)⁴ ·  )⁵꞉ (-x³· x⁷)³.
)⁵꞉ (-x³· x⁷)³.3.Преобразуйте выражение в одночлен стандартного видв:
1)-
 a²b⁴ · 4
a²b⁴ · 4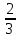 a³b⁷ ; 2) (-2
a³b⁷ ; 2) (-2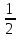 x³y⁵z)²·8x⁶z⁷;
x³y⁵z)²·8x⁶z⁷;4. Решите уравнение: (x²-3x+5)-(4x²-2x-8)=2-x-3x²
5.Вычислите: 1).
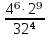 2). (2
2). (2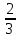 )⁵·(
)⁵·(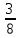 )⁶; 3).
)⁶; 3).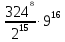
6.Вместо звездочки запишите такой многочлен, чтобы после приведения подобных членов полученный многочлен не содержал переменной x: 7x²-8x²y-3yz+*
7.Докажите, что при любом натуральном значении n остаток от деления значения выражения (3n+8)-(6-2n) на 5 равен 2.
8. Докажите, что не существует таких значений x и y, при которых многочлены
4x²-8x²y-3y² и -2x²+8x²y+8y² одновременно принимают отрицательные значения
Вариант 2. 1. Вычислите: (4⁴꞉100+0,06²·100)꞉0,2³
2. Представьте в виде степени с основанием x выражение:
1). (x⁴)³·(x⁴·x⁶)³ ; 2)
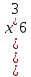 ·x⁴ ; 3)(-x³)⁶·(-x⁶)³꞉(-x³·x⁴)⁵.
·x⁴ ; 3)(-x³)⁶·(-x⁶)³꞉(-x³·x⁴)⁵.3.Преобразуйте выражение в одночлен стандартного вида:
1)
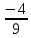 x⁵y⁷·6
x⁵y⁷·6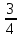 xy⁴ 2)(-3
xy⁴ 2)(-3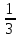 a⁴bc⁶)³·27b⁷c⁵
a⁴bc⁶)³·27b⁷c⁵4.Решите уравнение: (y²+4y-9)-(8y²-9y-5)=8+13y-7y²
5.Вычислите :1)
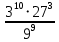 2) (5
2) (5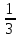 )⁷·(
)⁷·( )⁸ 3)
)⁸ 3)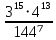
6.Вместо звездочки запишите такой многочлен, чтобы после приведения подобных членов полученный многочлен не содержал переменной y: 8y³-7x³y²+3x³z+*
7.Докажите, что при любом натуральном значении n остаток от деления значения выражения (2n+7)-(4-5n) на 7 равен 3
8. Докажите, что не существует таких значений x и y . при которых многочлены
-5x²+4xy³-8y² и 3x²-4xy³+3y² одновременно принимают положительные значения.
Контрольная работа №3 по теме «Целые выражения»
Вариант1
1Представьте в виде многочлена выражение:
1).-3a(2a-b); 2) 2x²y(4x³+5xy²-y²); 3)(x-2)(2x+3); 4) (y+3)(y²+y-6)
2. Разложите на множители:
1)12a²b³-18a⁵b²; 2) (b²-7)²-b(b²-7); 3) 8x+8y-ax-ay; 4) 8m⁷-6v²n-12m⁵n³+9n⁴.
3.Решите уравнение (3x-5)(2x+7)=(3x+1)(2x-3)+4x.
4.Решите уравнение 10x²-5x=a, если один из его корней равен 0,5
5.Докажите, что значение выражения 32³+8⁶ кратно 9.
6.Вынесите за скобки общий множитель (n-натуральное число):
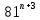 _
_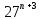 +
+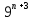
7.Разложите на множители трехчлен:
1)x²-12x+20; 2)2x²-3x-2.
Вариант 2
1.Представьте в виде многочлена выражение:
1) -4x(x+2y); 2) 3a³b(3a⁴-4a³b+b⁵) ; 3) (7x-3y)(2x+5y); 4) (x-1)(x²-x-2).
2.Разложите на множители:
1)14x⁴y⁵-21x²y⁷; 2)(a²+4)-a(a²+4); 3)(am-an-4m+4n ; 4) 6a⁴b+9a³-10a⁸b-15a⁷.
3.Решите уравнение (4x-1)(3x-2)=(6x+1)(2x+3)-4x
4.Решите уравнение 8x²+12x=b, если один из его корней равен-1,5.
5.Докажите, что значение выражения 81⁵-27⁶ кратно 8.
6.Вынесите за скобки общий множитель(m-натуральное число)
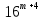 +
+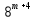 -
-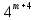
7.Разложите на множители трехчлен:
1)10 x²+15x+50 2)2x² -5x+2
Контрольная работа №4 по теме «Целые выражения»
Вариант 1.
1.Представьте в виде многочлена выражение:
1)(2x+9)² ; 2)(3x³-4xy)(3x³+4y) ; 3)(-3a-8b)² ; 4) (-5m²-7n⁵)(5m⁵-7n⁵).
2.Разложите на множители многочлен:
1)16c²-9 2)-25
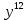 +4
+4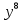 3)36a⁶-60a³b⁵+25
3)36a⁶-60a³b⁵+25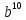
3.Решите уравнение:
1) (5x-1)(x+2)+3(x-4)(x+4)=2(2x+3)²-8;
2) (7x-6)²-81=0;
3) (6c-4)²-(4c+3)²=0;
4) (x-3)²+(x+2)²=2(3-x)(x+2);
4.Докажите ,что уравнение x²-6x+13=0 не имеет корней.
5. Известно, что a²+b²+c²=17 и a-b-c=5. Найдите значение выражения bc-ab-ac.
Вариант 2.
1.Представьте в виде многочлена выражение:
1) (4m-5)² 2)(4a-5b²)(4a+5b²) 3) (-7m-4n)² 4) (3x⁴-8y⁷)(-3x⁴-8y⁷).
2.Разложите на множители многочлен:
1)25-4a² ; 2)-36
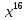 +9y⁴ ; 3)49c⁸-84c⁴d⁵+36
+9y⁴ ; 3)49c⁸-84c⁴d⁵+36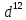 .
.3.Решите уравнение:
1)(7x+1)(x-3)+20(x-1)(x+1)=3(3x-2)²+13
2)(3x+5)²-64=0
3)(3z+5)²-(4z-7)²=0
4)(x+4)²+(x-8)²=2(8-x)(x+4).
4.Докажите, что уравнение x²+4x+7=0 не имеет корней.
5.Известно,что a-b+c=8 и ac-ab-bc=21. Найдите значение выражения a²+b²+c².
Контрольная работа №5 по теме « Целые выражения».
Вариант 1.
1.Разложите на множители выражение:
1)4ab²-9a³ 2) x³+8y³ 3) c⁸+32.
2.Представьте в виде многочлена выражение (-2m+5)³.
3.Упростите выражение: a(a+2)(a-2)-(a-3)(a²+3a=9).
4.Разложите на множители выражение:
1) x-3y+x² -9y² 2) 1-x²+10xy-25y² 3)(x+5)³ -64.
5.Решите уравнение:
1) 49x³+14x²+x=0 2)x³-5x²-x+5=0 3)x³-3x²+3x-2=0
6.Докажите,что при любом натуральном n значение выражения
9ⁿ+17ⁿ-2 кратно 8
7.Разложите на множители многочлен 2a³+3a²b+3ab²+b⁸.
Вариант 2.
1.Разложите на множители выражение:
1) 25x⁵-16x³y³ 2)27x³-y³ 3) 243x⁵-1.
2.Представьте в виде многочлена выражение: (-3+4x)³.
3.Упростите выражение x(x-1)(x-1)-(x-2)(x²+2x+4).
4.Разложите на множители выражение:
1)7m-n+49m²-n² 2)9-x²-2xy-y³ 3)(x-4)³-27.
5. Решите уравнение:
1)64x³-16x²+x=0 2) x³-3x²-4x+12=0 3)x³+6x²+12x+9=0.
6.Докажите, что при любом натуральном n значение выражения 10ⁿ+19ⁿ-2 кратно 9.
7.Разложите на множители многочлен 9m³+3m²n+3mn²+n³
Контрольная работа № 6 по теме «Функции»
Вариант 1.
1.Линейная функция задана формулой y=-0,6x+3. Не выполняя построения, найдите:
1) какие из данных точек принадлежат графику функции: А(-2;4,2); В(1;3,6); С(10;-3).
2)координаты точек пересечения графика функции с осями координат.
2.Постройте график функции y=2x-4. Пользуясь графиком, найдите:
1)значение функции, если значение аргумента равно 3;-1;0,5.
2)значение аргумента, при котором значение функции равно 2;-2; 0;
3)Значения аргумента, при котором функция принимает положительные значения.
3.Какие из следующих утверждений верны:
1) 4
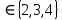
2)
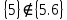 3)
3)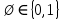 ?
?4. При каком значении k график функции y=kx+5 проходит через точку D(6;-19) ?
5.При каком значении переменной x f(x)=3x-1 g(x)=0,5x+4 принимают равные значения Постройте на одной координатной плоскости графики функций f и g. Определите, при каких значениях x
1)f(x)
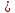 g(x) 2)f(x)
g(x) 2)f(x)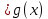
6.Функция задана формулой y=x²+3x-4. При каких значение функции равно утроенному значению аргумента?
7.Постройте график функции: 1) y =
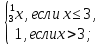 2) y=|x|+2x.
2) y=|x|+2x.Вариант 2
1.Линейная функция задана формулой y=-0,4 x+2. Не выполняя построения, найдите:
1) какие из данных точек принадлежат графику функции: А(-2;1,2); В(1;3,6); С(10;-2).
2)координаты точек пересечения графика функции с осями координат.
2.Постройте график функции y=5x-4. Пользуясь графиком, найдите:
1)значение функции, если значение аргумента равно1;-1;0,5.
2)значение аргумента, при котором значение функции равно 6;-9; 0,5;
3)Значения аргумента, при котором функция принимает положительные значения.
3.Какие из следующих утверждений верны:
1) 6
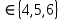
2)
 3)
3) ?
?4.При каком значении k график функции y=k x-15 проходит через точку C(-2;-3)?
5.При каком значении переменной x функции f(x)=2 x-6 g(x)=-0,4x +6 принимают равные значения Постройте на одной координатной плоскости графики функций f и g. Определите, при каких значениях x