Файл: Практическая работа 1 Теоретические основы моделирования. Регрессионный и корреляционный анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 797
Скачиваний: 79
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическая работа № 2
Линейная оптимизация.
Вариант 1
Целевая функция – максимум прибыли, расход и ресурсные ограничения по видам сырья.
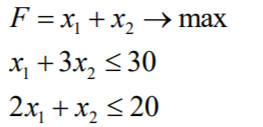
Задаем ограничения:
-
x1+3x2
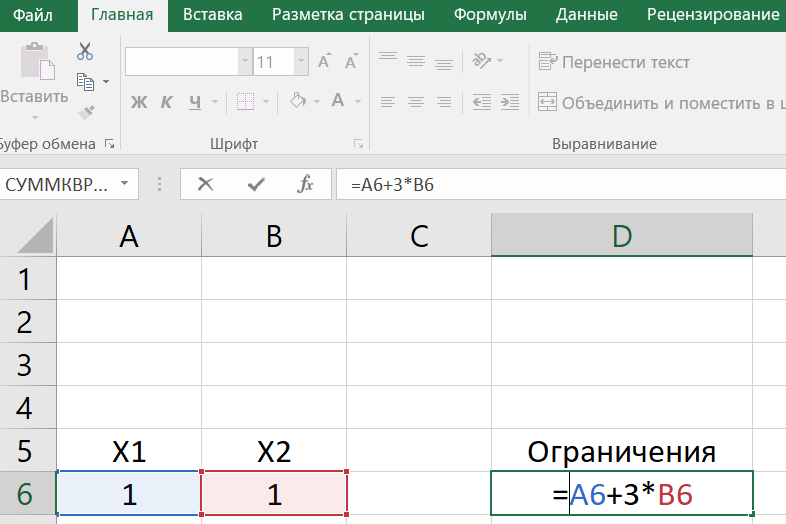
-
2x1+x2
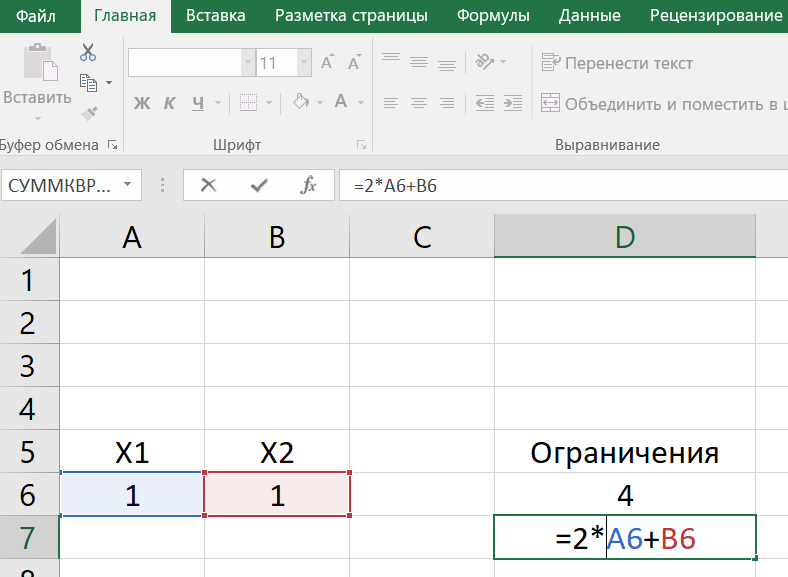
-
Задаем целевую функцию:
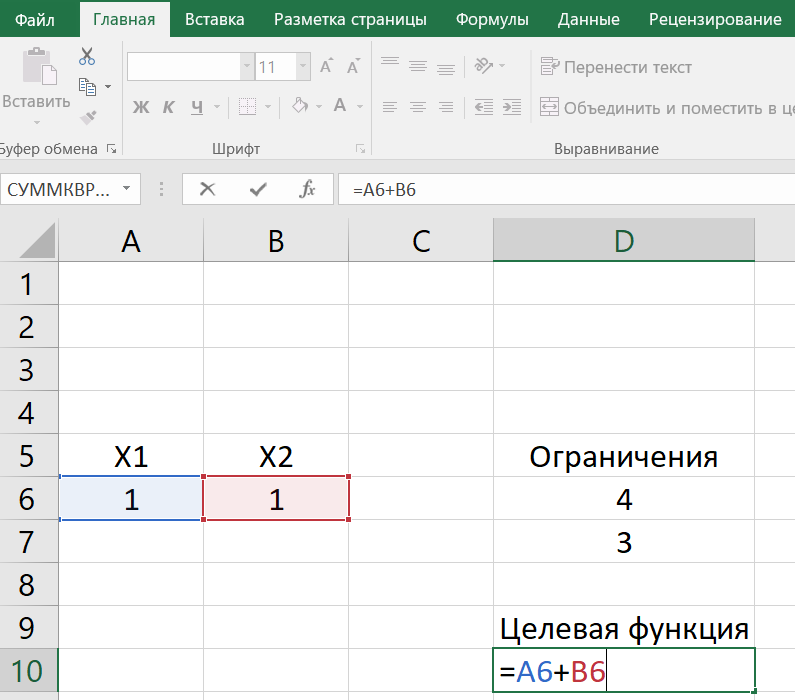
-
Настраиваем «Поиск решения»
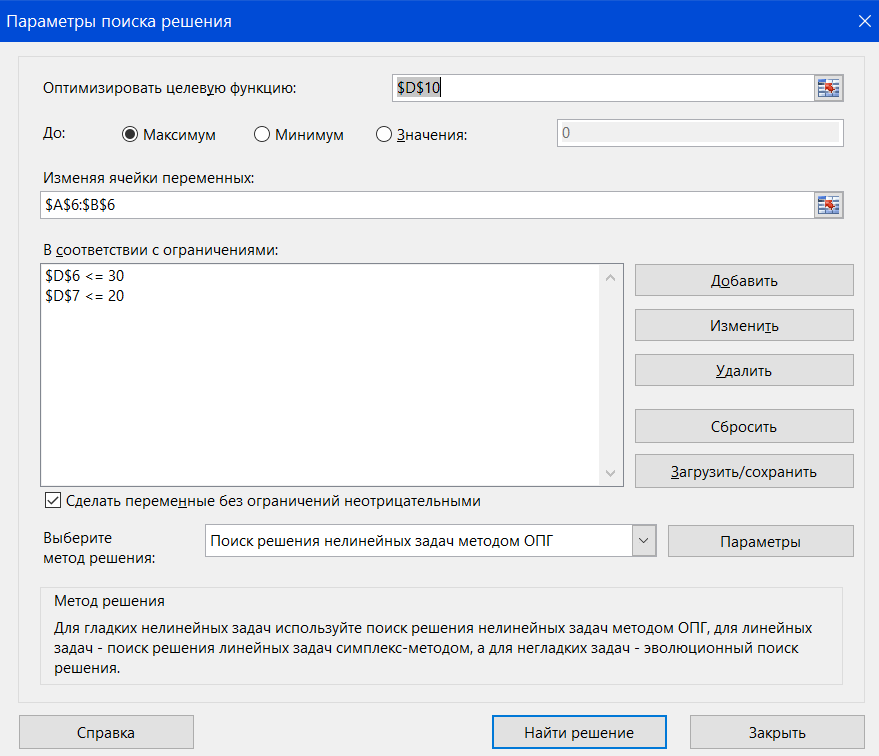
-
Получаем решение:
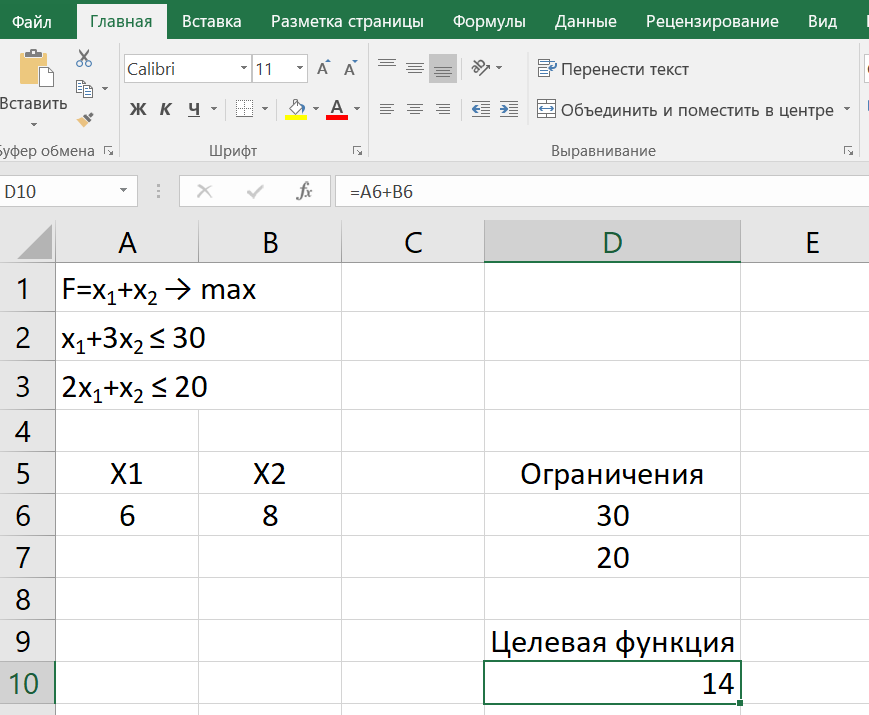
Вопросы для проверки:
-
Назовите основные методы решения ЗЛП.
Графический метод решения задачи линейного программирования основан на геометрической интерпретации ЗЛП и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно
Наиболее известным и широко применяемым на практике для решения общей ЗЛП является симплекс-метод. Несмотря на то, что симплекс-метод является достаточно эффективным алгоритмом, показавшим хорошие результаты при решении прикладных задач ЛП, он является алгоритмом с экспоненциальной сложностью. Причина этого состоит в комбинаторном характере симплекс-метода, последовательно перебирающего вершины многогранника допустимых решений при поиске оптимального решения.
Первый полиномиальный алгоритм, метод эллипсоидов
, был предложен в 1979 г. советским математиком Л. Хачияном, разрешив таким образом проблему, долгое время остававшуюся нерешённой. Метод эллипсоидов имеет совершенно другую, нежели симплекс-метод, некомбинаторную природу. Однако в вычислительном плане этот метод оказался неперспективным. Тем не менее, сам факт полиномиальной сложности задач привёл к созданию целого класса эффективных алгоритмов ЛП — методов внутренней точки, первым из которых был алгоритм Н. Кармаркара, предложенный в 1984 году. Алгоритмы этого типа используют непрерывную трактовку ЗЛП, когда вместо перебора вершин многогранника решений ЗЛП осуществляется поиск вдоль траекторий в пространстве переменных задачи, не проходящих через вершины многогранника.
-
Поясните суть симплекс-метода решения ЗЛП.
Суть симплекс-метода заключается в том, что решение ЗЛП осуществляется итерационно и основывается на переходе от одного допустимого базисного решения к другому, при котором значение целевой функции улучшается. Этот процесс длится до тех пор, пока дальнейшее улучшение целевой функции станет невозможно.
В алгебраических терминах симплекс-метод предполагает:
1) умение находить начальный опорный план;
2) наличие признака оптимальности опорного плана;
3) умение переходить к нехудшему опорному плану.
Геометрический смысл симплекс-метода состоит в последовательном переходе от одной вершины многогранника ОДР к соседней, в которой целевая функция принимает лучшее значение, до тех пор, пока не будет найдено оптимальное решение.
Симплексный метод универсален, поскольку позволяет решить любую ЗЛП.
-
Поясните суть графического решения ЗЛП.
Этот метод применяется для решения ЗЛП с двумя переменными, заданными в неканонической форме и многими переменными в канонической форме, при условии, что они содержат не более двух свободных переменных. Метод основывается на возможности графического изображения области допустимых решений задачи и нахождении среди них оптимального решения(ОДР). ОДР задачи – это ОДР системы неравенств и равенств ограничений. Для нахождения среди ДР оптимального решения используют линии уровня и опорные прямые. Линией уровня называется прямая, на которой целевая функция задачи принимает постоянное значение. Уравнение линии уровня в общем случае имеет вид
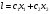 . Все линии уровня параллельны между собой. Их нормаль
. Все линии уровня параллельны между собой. Их нормаль- 1 2 3
Могут ли ответы в решении ЗЛП быть отрицательными и почему?
Если все оценки индексной строки (строки целевой функции) не отрицательны, то соответствующий план является оптимальным в задаче максимизации. Признак оптимальности задачи минимизации: Если все оценки индексной строки (строки целевой функции) не положительны, то соответствующий план является оптимальным в задаче минимизации.
-
Какие ресурсные ограничения используются в задачах ЗЛП?
Основными ресурсными ограничениями в задачах ЗЛП являются материальные ресурсы(деньги, материалы, сырье), время, рабочая сила.
Практическая работа № 3
Транспортная задача.
Задание: Определить оптимальный план перевозок с минимальными затратами для исходных данных, приведенных ниже.
Вариант 2
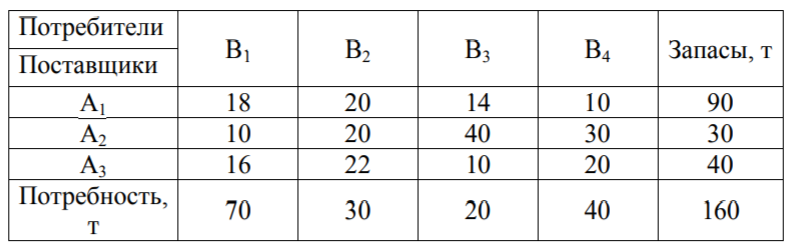
-
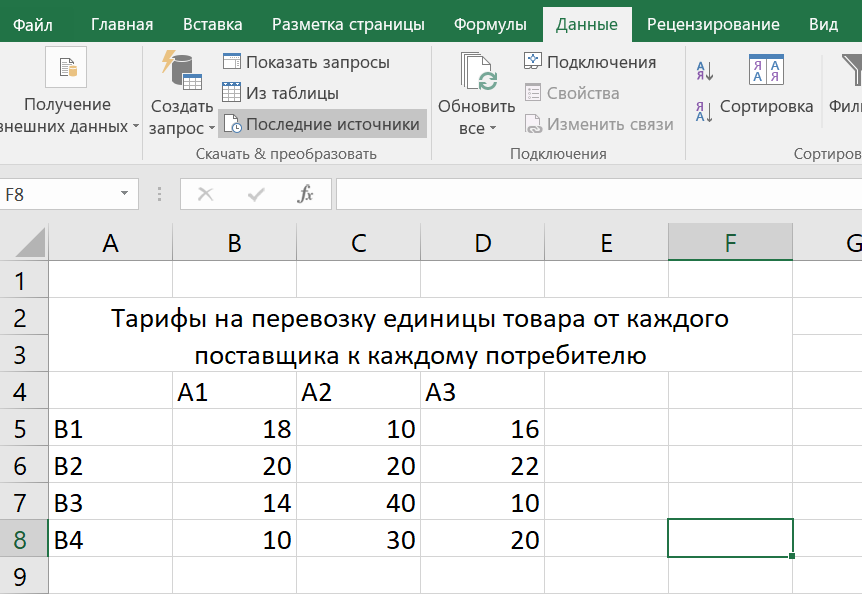
Указываем тарифы на перевозку единицы товара от каждого поставщика к каждому потребителю:
-
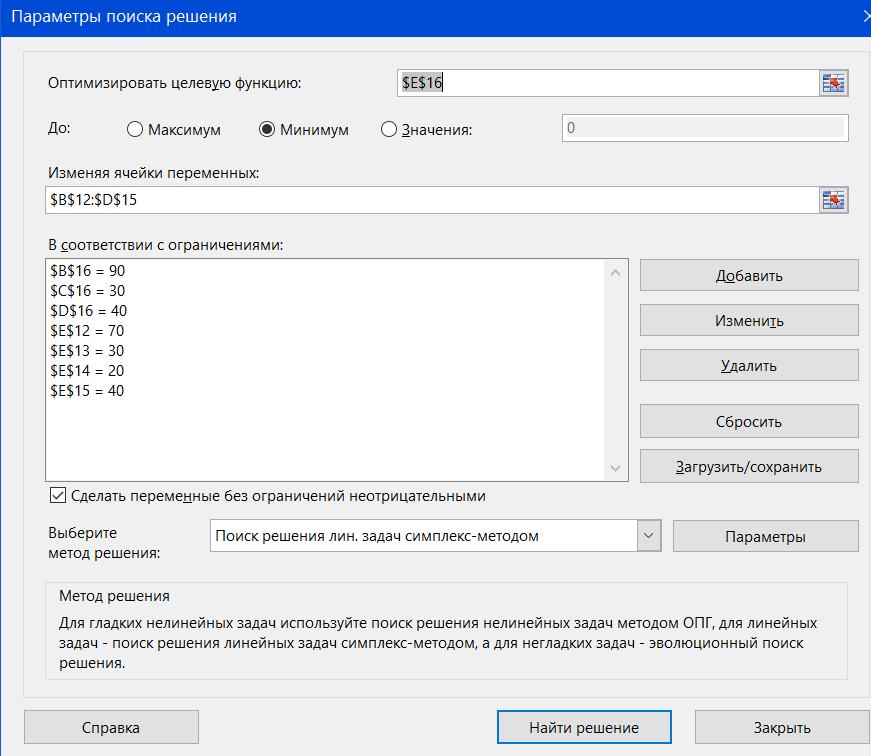
Настраиваем «Поиск решения»
-
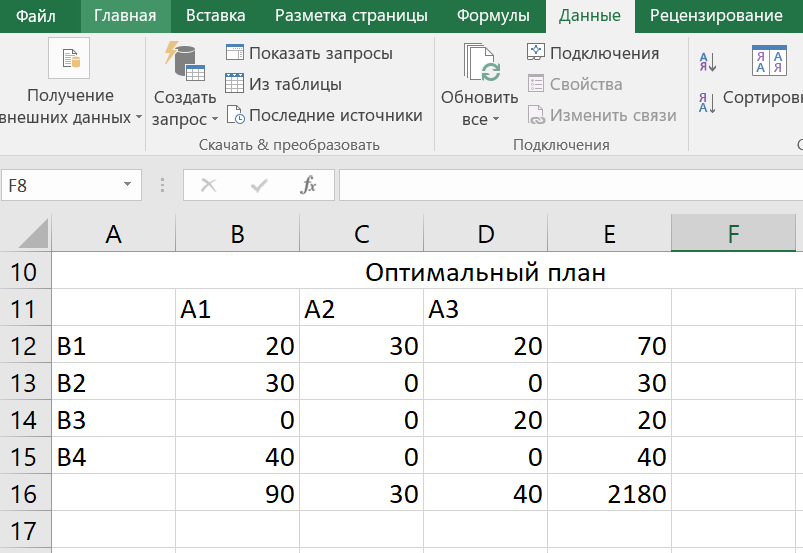
Получаем оптимальные объемы перевозок и минимальное значение целевой функции:
Вопросы для проверки:
-
Какие задачи линейного программирования называются транспортными?
Транспортная задача – это задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи).
Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку). Под названием транспортная задача, определяется широкий круг задач с единой математической моделью, эти задачи относятся к задачам линейного программирования и могут быть решены оптимальным методом. Однако, специальный метод решения транспортной задачи позволяет существенно упростить её решение, поскольку транспортная задача разрабатывалась для минимизации стоимости перевозок.
-
Каковы особенности математической модели транспортной задачи?
Однородный груз сосредоточен у m поставщиков в объемах
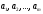 Данный груз необходимо доставить n потребителям в объемах
Данный груз необходимо доставить n потребителям в объемах 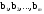 . Известны
. Известны 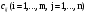 - стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и суммарные затраты на перевозку всех грузов минимальны.
- стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и суммарные затраты на перевозку всех грузов минимальны.Исходные данные транспортной задачи записываются в таблице вида:
| | | | … | |
| | | | … | |
| | | | … | |
| … | … | … | … | … |
| | | | … | |