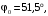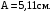МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Уфимский государственный нефтяной технический университет» (ФГБОУ ВО УГНТУ)

Институт нефтепереработки и нефтехимии ФГБОУ ВО УГНТУ в г. Салавате

Кафедра «Информационных технологий»

Физика
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
Классическая механика
ИнТех- 18.03.02 – 1.01.07 РГР

Исполнитель:

студент гр. БМОз - 22-21 В.А. Медведев

Руководитель:

ассистент Г.Ф. Шаяхметов

Салават

2023

расчетное задание № 1

Классическая механика

1.7. Материальная точка движется по окружности с постоянной угловой скоростью w = л/6 (рад/с). Во сколько раз путь s , пройденный точкой за время t=4 с, будет больше модуля ее перемещения r? Принять, что в момент начала отсчета времени радиус-вектор r, задающий положение точки на окружности, относительно исходного положения был повернут на угол  = /3 рад.

Дано: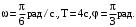

СИ: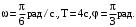

Найти: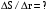

Решение:


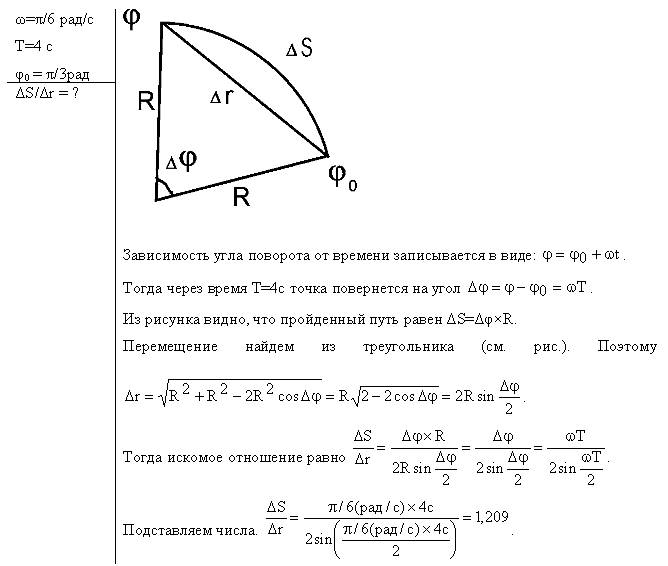
Зависимость угла поворота от времени записывается в виде:
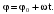(1)
Тогда через время Т=4с точка повернется на угол
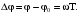(2)
Из рисунка видно, что пройденный путь равен
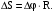(3)
Перемещение найдем из треугольника (см. рисунок). Поэтому
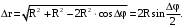(4)
Тогда искомое отношение равно
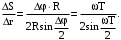(5)
Проверим размерности расчетных формул



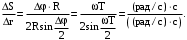
Подставляем числа.



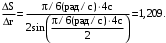
Ответ: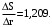
1.17. Снаряд, летевший со скоростью v = 400м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью v₁ = 150м/с. Определить скорость v₂ большего осколка.

Дано: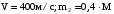

СИ: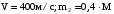



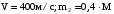
Найти: V₂=?

Решение:


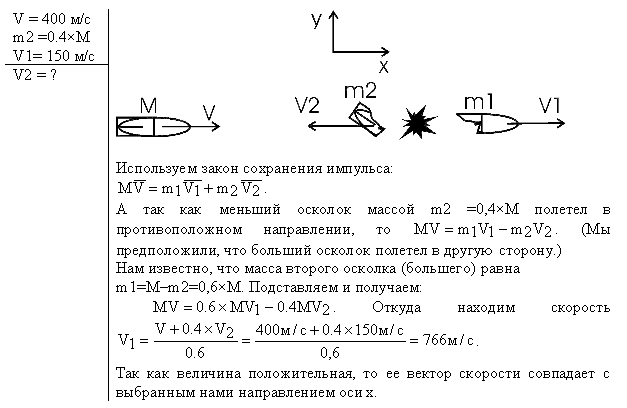
Используем закон сохранения импульса:
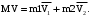(6)
А так как меньший осколок массой
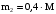(7)
полетел в противоположном направлении, то
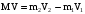. (8)
(Мы предположили, что большой осколок полетел в другую сторону.)

Нам известно, что масса второго осколка (больше) равна
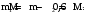(9)
Подставляем и получаем:
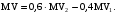(10)
Откуда находим скорость

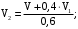(11)
Проверим размерности расчетных формул



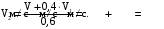
Подставляем числа.



Так как величина положительная, то ее вектор скорости совпадает с выбранным нами направлением оси х.

Ответ: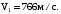
1.27. Из ствола автоматического пистолета вылетела пуля массой m₁ = 10г со скоростью v = 300м/с. Затвор пистолета массой m₂ = 200г прижимается к стволу пружиной, жесткость которой k = 25кН/м. На какое расстояние отойдёт затвор после выстрела? Считать, что пистолет жестко закреплен.

Дано: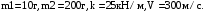

СИ: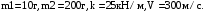

Найти: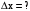

Решение:

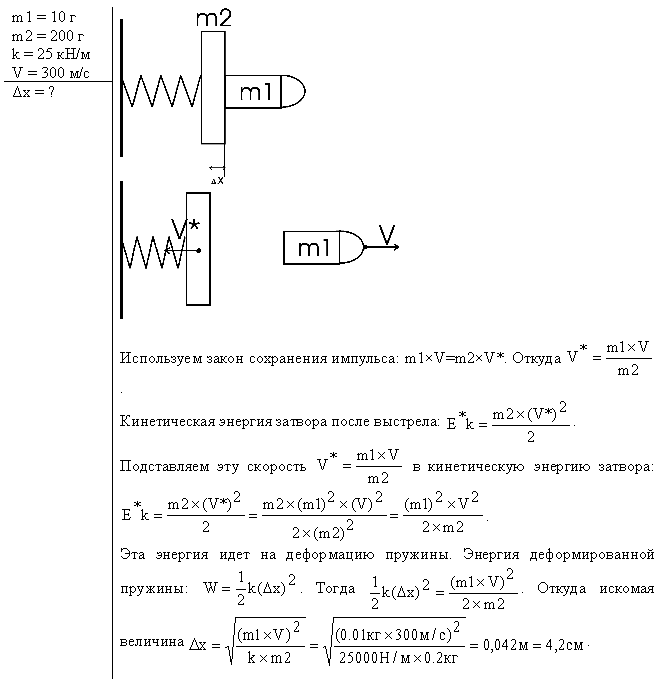
Используем закон сохранения импульса:

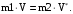(12)

Откуда

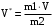(13)

в кинетическую энергию затвора:
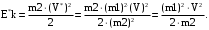(14)
Эта энергия идет на деформацию пружины. Энергия деформированной пружины:
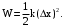(15)
Тогда
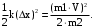(16)
Откуда искомая величина
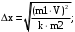(17)
Проверим размерности расчетных формул



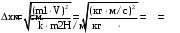
Подставляем числа.



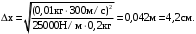
Ответ:
1.37. Из пружинного пистолета с пружиной жесткостью k = 150 Н/м был произведен выстрел пулей массой m = 8г. Определить скорость и пули при вылете ее из пистолета, если пружина была сжата на х = 4см.

Дано: k=150 Н/м; m=8 г; ∆x=4 см;

СИ: m=0,008 г; ∆x=0,04 м;

Найти: v-?

Решение:


Кинетическая энергия пули после выстрела:

где v – скорость пули.

Эта энергия идет на деформацию пружины. Энергия деформированной пружины:

Тогда


Откуда искомая величина равна


Проверим размерности расчетных формул



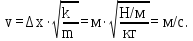
Подставляем числа.



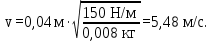
Ответ: v=5,48 м/с.

1.47. Определить момент силы М, который необходимо приложить к блоку, вращающемуся с частотой n = 12с^-1 , чтобы он остановился в течение времени
t = 8с. Диаметр блока D = 30см. Массу блока m = 6кг считать равномерно распределенной по ободу.

Дано: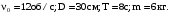

СИ: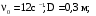

Найти: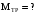

Решение:

Из второго закона Ньютона, применяемого к вращающимся телам, находим:
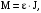(22)
где М - момент сил;

- угловое ускорение;

J – момент инерции диска.

Момент инерции однородного диска массой m и радиусом R равен
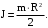(23)
Поэтому
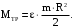(24)
Зависимость угловой скорости при равнозамедленном вращении записывается в виде
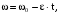(25)
где 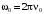- начальная угловая скорость.

Известно, что через время t=8 с диск остановился и 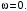Поэтому
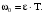(26)
Откуда угловое ускорение равно
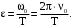(27)
Подставляем в
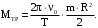(28)
Так как радиус
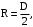(29)
то
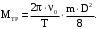(30)
Проверим размерности расчетных формул



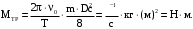
Подставляем числа.



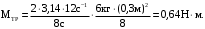
Ответ: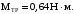
1.57. На краю платформы в виде диска, вращающейся по инерции вокруг вертикальной оси с частотой n₁ = 8 мин^-1 , стоит человек массой m₁ = 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n₂ = 10 мин ¹

---

Определить массу m₂; платформы. Момент инерции человека рассчитывать, как для материальной точки.

Дано:

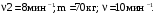
СИ:

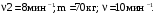
Найти: m₂=?

Решение:

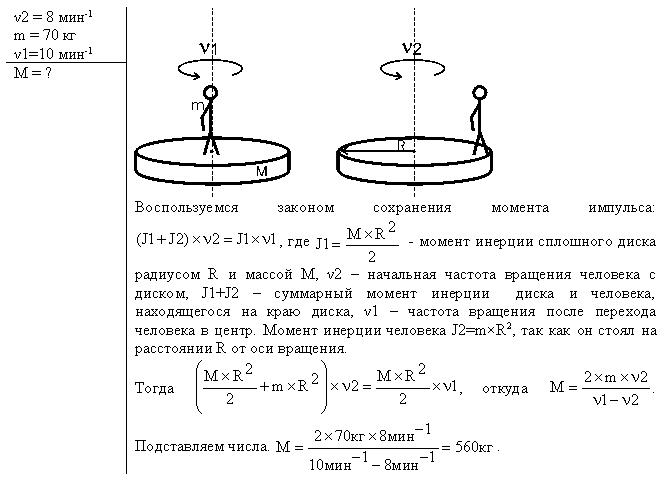
Воспользуемся законом сохранения момента импульса:
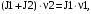(31)
где 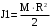- момент инерции сплошного диска радиусом R и массой М;

2 – начальная частота вращения человека с диском;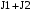

- суммарный момент инерции диска и человека, находящегося на краю диска;

1 – частота вращения после перехода человека в центр.

Момент инерции человека
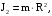(32)
так как он стоял на расстоянии R от оси вращения.

Тогда
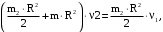(33)
откуда
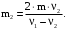(34)
Проверим размерности расчетных формул



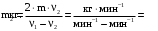
Подставляем числа.



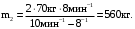
Ответ:
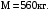
1.67. Спутник обращается вокруг Земли по круговой орбите на высоте h = 520 км. Определить период обращения спутника. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.

Дано:

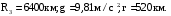
СИ:

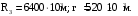
Найти:

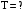
Решение:


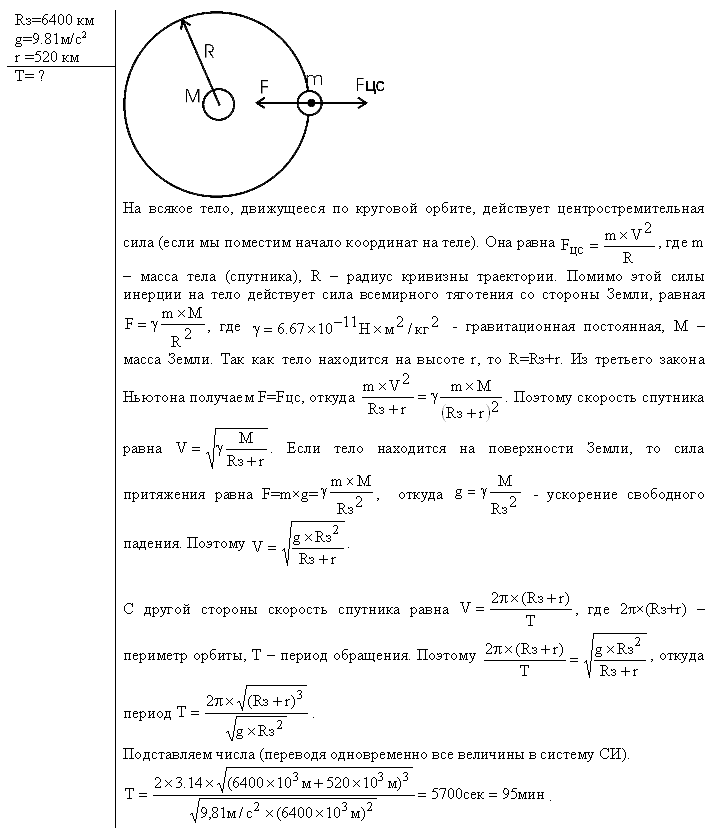
На всякое тело, движущееся по круговой орбите, действует центростремительная сила (если мы поместим начало координат на теле). Она равна
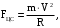(35)

где m – масса тела (спутника).

R – радиус кривизны траектории.

---

Помимо этой силы инерции на тело действует сила всемирного тяготения со стороны Земли, равная
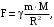(36)
где 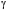=6,67·10^-11 Н·м²/кг² – гравитационная постоянная;

М – масса Земли.

Так как тело находится на высоте r, то

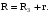(37)
Из третьего закона Ньютона получаем
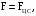(38)
откуда
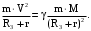(39)
Поэтому скорость спутника равна
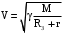. (40)
Если тело находится на поверхности Земли, то сила притяжения равна
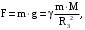(41)
откуда
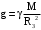- ускорение свободного падения.

Поэтому
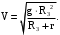(42)

C другой стороны скорость спутника равна
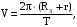(43)
где 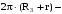пример орбиты;

Т – период обращения.

Поэтому
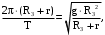(44)
откуда период
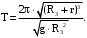(45)
Проверим размерности расчетных формул



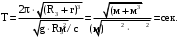
Подставляем числа.



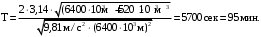
Ответ:
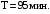
1.77. Материальная точка совершает простые гармони­ческие колебания так, что в начальный момент времени смещение х₀ = 4 см, а скорость v₀ = 10 см/с. Определить амплитуду А и начальную фазу ₀ колебаний, если их период Т = 2 с.

Дано:

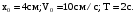
СИ:

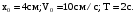
Найти:

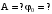
Решение:

Уравнение гармонических колебаний
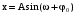, (46)
где х – смещение колеблющейся величины;

А – амплитуда колебаний;

---

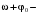
фаза колебаний;



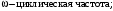
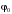– начальная фаза.

Скорость равна
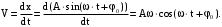(47)
В начальный момент T=0 имеем
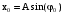(48)
и
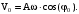(49)
Поделим начальное смещение на скорость и получим
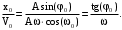(50)
Циклическая частота равна по определению
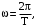(51)
где Т – период.

Поэтому
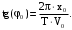(52)
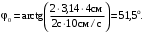(53)
Теперь найдем амплитуду. Умножим
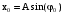(54)
на 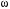, возведем все в квадрат и сложим с
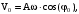(55)
возведенным в квадрат.

Получим следующее:
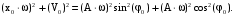(56)
Так как
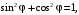(57)
то

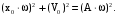(58)
Откуда амплитуда равна

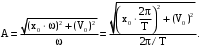(59)
Проверим размерности расчетных формул



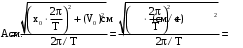
Подставляем числа.



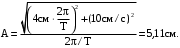
Ответ:

---

Смотрите также файлы

• Ю. И. Богданов Физико статистические основы.pdf

• Курсовая работа Описание Анализ документооборота в организации Моя организация ооо "Такстелеком",больше известная под брендом такси максим.docx

• 2. 2 Мотивация деятельности.docx

• Текст с егэ 9 (егэ 2021).docx

• Исследование конкурентоспособности предприятия на примере ооо Невельский морской торговый порт.docx