МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Контрольная работа по предмету

«Высшая математика»

Вариант №18


Выполнил:

Студент  
Зач.кн.

Проверил:


2022 г.

Вариант 18

1. Вычислить:
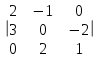
Вычислим определитель методом треугольников:




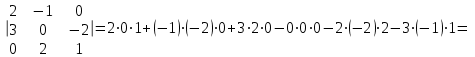
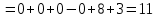
2. Найти сумму элементов матрицы 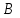, если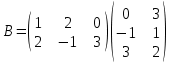



Находим матрицу :



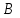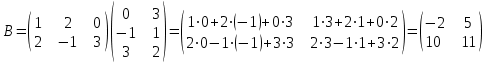
Сумма элементов матрицы :



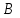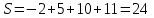
3. Решить систему уравнений, приняв в качестве базисных переменных 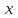и :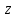


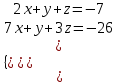
Методом исключения неизвестных найдем выражения зависимых (базисных) переменных через свободные








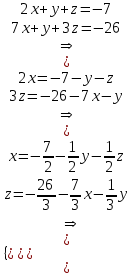
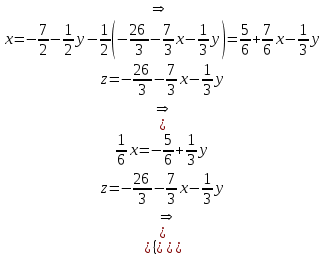
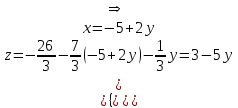
4. Вычислить 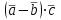, если , ,

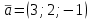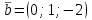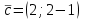
Найдем :



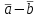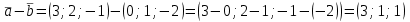
Тогдаскалярное произведение:

---

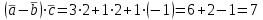
5. Найти площадь треугольника с вершинами в точках , ,
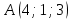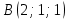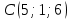
Площадь треугольника 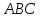определим по формуле 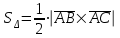. Находим векторное произведение векторов 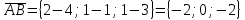и :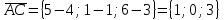

.

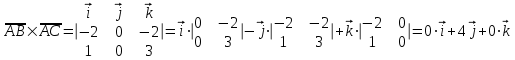Тогда .

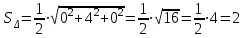6. Найти объем треугольной пирамиды с вершинами в точках , , ,
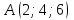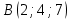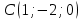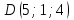
Объем треугольной пирамиды найдем через смешанное произведение векторов по формуле .

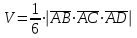Найдем смешанное произведение векторов 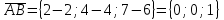, 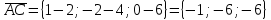и :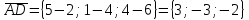

.

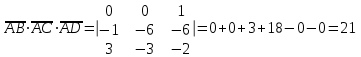Тогда искомый объем .

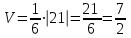7. Прямые 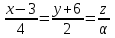и 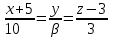параллельны. Найти .

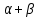Если две прямые в трехмерном пространстве параллельны, значит их направляющие векторы коллинеарны.

Направляющий вектор первой прямой 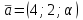, второй прямой – .

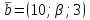Два вектора коллинеарны, если отношения их координат равны:

---

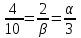
Отсюда находим, что , .

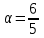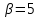Следовательно: .


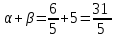8. Составить уравнение плоскости, проходящей через точку 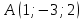, перпендикулярно прямой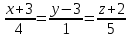
Из канонических уравнений прямой находим координаты ее направляющего вектора 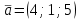. Поскольку искомая плоскость проходит перпендикулярно прямой, то ее нормальным вектором будет направляющий вектор прямой, т.е. .

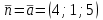А уравнение плоскости, которая проходит через точку 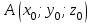и имеет нормальный вектор 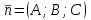, имеет вид: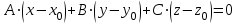



Подставляя соответствующие значения, получим:

.

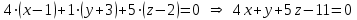9.

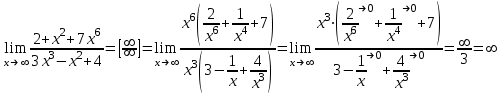
10. Найти 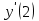, если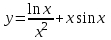
Находим производную:







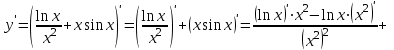
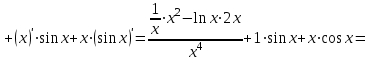
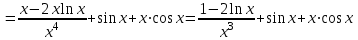
Тогда



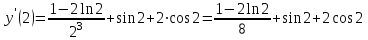
11. Для функци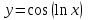и найти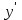


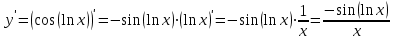
12. Найти интервал(ы) убывания функции
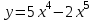
Найдем производную заданной функции:



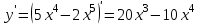
Найдем критические точки из уравнения

---

:



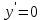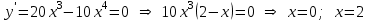
Таким образом, получили две критических точки.

Нанесем эти точки на числовую ось и исследуем знак производной слева и справа от каждой из них:




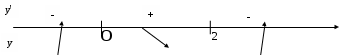
Поскольку при 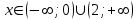производная 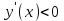, то на этих интервалах функция убывает.
13. Для функци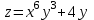и найти 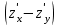в точке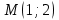
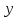Найдем частные производные первого порядка данной функции. При нахождении частной производной по переменную считаем постоянной, а при нахождении частной производной 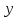переменную считаем постоянной: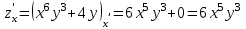

;

.

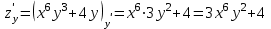Тогда



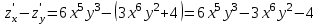
В точке :

---

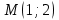Смотрите также файлы

• Программа среднего профессионального образования Дисциплина Основы философии Практическое занятие 2.doc

• Что такое античность и в чём особенности возникновения и развития античной цивилизации.docx

• Профессиограмма Трудограмма (описание труда в профессии) Предназначение профессии Психолог.docx

• Пп Пункт предложения.pdf

• Правовые методы природопользования Проблема охраны окружающей среды уже давно перестала быть только естественнонаучной и всё чаще затрагивает различные социальные и политические аспекты. Взаимосвязь экологии и права.pptx