Добавлен: 23.11.2023
Просмотров: 94
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- т.к. одно состояние не может перейти в другое состояние, если не произошло какое-либо действие.
- т.к. результатом действия не может быть другое действие, может быть только сущность или новое состояние. Если в переход входит несколько дуг, они символизируют условие для выполнения действия и связаны союзом «и».
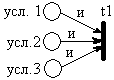
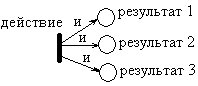
Если в состояние входит несколько дуг, они символизируют одно из действий, выполнение которого приведет к наступлению данного состояния и связаны союзом «или».
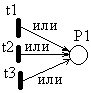
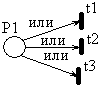
Каждая позиция может быть маркирована, т.е. содержать некоторое количество маркеров (фишек, точек, меток). Рi
Маркер – знак выполнения соответствующего условия и имеет смысл указания мощности потоков.
Если обозначить количество фишек, находящихся в позиции pi, как mi, то маркировка всей сети: M = {m1, m2… mn}. Тогда полное определение сети Петри, включая данные о начальной маркировке, можно записать в виде
PN = (N, M0),
где М0 – начальная маркировка сети.
При выполнении условий переходы срабатывают, действия выполняются.
Правила срабатывания переходов:
Переход срабатывает только в том случае, если во всех входных позициях имеется достаточное количество меток (по меньшей мере, по одной). При срабатывании перехода из входных позиций изымаются метки (в случае взвешенной СП изымается количество меток, соответствующее весам дуг, связывающих входные позиции с данным переходом), а во входные – добавляются (для взвешенной СП – также соответственно весам дуг).
При срабатывании перехода из всех выходных позиций изымается по одному маркеру и помещается по одному маркеру во входные позиции. Это символизирует результат выполнения действия.
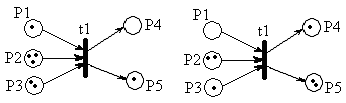
Веса дуг символизируют количество маркеров, которые переходят по ним.
Правила переходов для взвешенной цепи Петри:
Для срабатывания перехода необходимо, чтобы во всех входных позициях количество маркеров было не меньше весов соответствующих дуг.
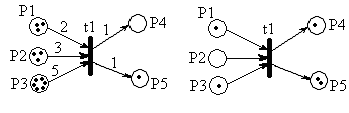
При моделировании процессов принятия решений с помощью СП ее позиции интерпретируют собой некоторые условия, состояния, значения переменных и т.д. Переходы интерпретируют собой логические предложения (принятие решений), соответствующие выполнению действий, при этом входные позиции – условия выполнения действий, выходные позиции – результат выполнения действий. Действие (переход) связано с принятием какого-либо решения, которое инициировано определенными условиями и результатом которого является новое состояние (условие).
Схема принятия решений при попытке получить деньги из банкомата.
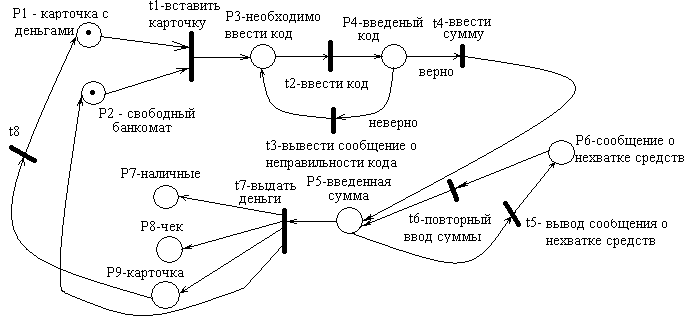
Начальная маркировка СП есть начальное состояние системы.
Таким образом, если осуществить начальную маркировку СП, то использованием формальных правил можно описать логику работы системы и произвести анализ ее работоспособности. Переходы меток описываются графом достижимости (ГД), у которого каждой вершине соответствует определенная маркировка, а каждой дуге – переход, который срабатывает при данной маркировке.
Таким образом, граф достижимости представляется как
GD = (V, E),
где V – массив (множество) вершин (маркировок, соответствующих вершинам):
V = {М1, М2 … Мq},
Мi – i-я маркировка, q – количество маркировок;
Е = {e1, e2 … ep} – массив дуг, связывающих вершины (р – количество дуг).
Каждая дуга представляется как совокупность ei = {1, 2, Т}, где 1 и 2 – номера начальной и конечной вершин графа; Т = {t1, t2, … tk} – массив переходов, соответствующий дуге; k – количество одновременно срабатывающих переходов при переходе от одной маркировки к другой.
Алгоритм построения графа по исходной СП:
1. За исходную берется маркировка М
0 и ей присваивается метка «новая».
2. Для каждой «новой» маркировки выполнять следующие операции:
2.1. определяются все переходы, которые могут быть запущены, а также все возможные комбинации этих переходов.
2.2. Для каждого разрешенного перехода или комбинации переходов производятся следующие действия:
2.2.1. Определяется маркировка М’, которая образуется при срабатывании данного перехода (комбинации переходов).
2.2.2. Просматриваются все маркировки в графе достижимости на пути от М’ к начальной М0. Если на пути находится маркировка Мi, элементы которой меньше соответствующих элементов маркировки М’, то эти элементы mi заменяются на символ «» (бесконечность), проводится дуга от новой маркировки к Мi и подписывается номером перехода.
2.2.3. Просматриваются все маркировки графа. Если находится маркировка Мi= М’ во всех элементах, то проводится дуга от новой маркировки к Мi и подписывается номером перехода.
Если в п.п. 2.2.2 и 2.2.3 маркировки не найдены, то создается новая вершина графа, которой соответствует маркировка М’, проводится дуга от новой маркировки к М’, помечается номер перехода, а самой М’ присваивается метка «новая».
Граф строится до тех пор, пока существуют маркировки с меткой «новая».
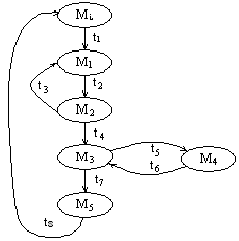
Таблица 4.3
| | (Р1 Р2 Р3 Р4 Р5 Р6 Р9) |
| М0 | (110000000) |
| М1 | (001000000) |
| М2 | (000100000) |
| М3 | (000010000) |
| М4 | (000001000) |
| М5 | (010000111) |
| М6 | (110000110) |
М0< М6
110000000 < 110000110
Переполнение в Р7 , Р8 М0 = (1100000)
С помощью ГД могут быть определены свойства СП и, в конечном счете, моделируемой системы. К ним относятся:
-
живость (отсутствие в графе достижимости тупиковых состояний);
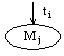- тупик. Сеть неживая. В реальной системе нет тупиковых состояний.- ограниченность (сеть ограниченна, если символ «» не входит ни в одну вершину графа), т.е. в реальной моделируемой системе нет бесконечного накопления какой-нибудь сущности;
- безопасность (сеть безопасна, если в маркировки входят только «0» и «1») – физически безопасность означает отсутствие зацикливаний;
- правильность (если сеть безопасная и живая, то она правильная);
- обратимость (сеть обратима, если в графе имеется хотя бы одна дуга, направленная к начальной маркировке М0);
- пассивность переходов (переход ti пассивен, если он не соответствует ни одной дуге графа достижимости, т.е. в реальной системе действие соответствующее этому переходу никогда не будет выполнено);
- число возможных состояний Nсост.
Сеть Петри называется k-ограниченной, если в любом состоянии в любой позиции скапливается не более k фишек.
Любая система должна представляться правильной сетью.
Для рассмотренного примера можно сделать вывод, что сеть правильная, обратимая и без пассивных переходов.
Практическое значение и наиболее ясную интерпретацию имеют два вида СП:
1) Маркированные графы – каждая позиция такой СП должна иметь не более одного входного и одного выходного перехода, т.е. в реальной системе нет выбора последующих действий;
2) А-сети (автоматные сети) – каждый переход такой СП должен иметь не более одной входной и одной выходной позиции (так моделируются различные автоматические устройства).
СП моделируют очень широкий класс логических задач. Существует много разновидностей сетей. Главное их достоинство – возможность анализировать логический процесс по неизбыточным моделям. Кроме того, формализованные методы анализа СП в сочетании с возможностью декомпозиции дают возможность решать очень сложные задачи принятия решений.
Построить сеть Петри, моделирующую работу рабочей станции, обслуживающей группу пользователей. Пользователь присылает заявку на обработку задания. Если станция свободна, она начинает обработку задания. После выполнения задания станция передает обслуженную заявку, освобождается и либо начинает обрабатывать новую заявку (если заявка поступила), либо ждет поступления новой заявки.
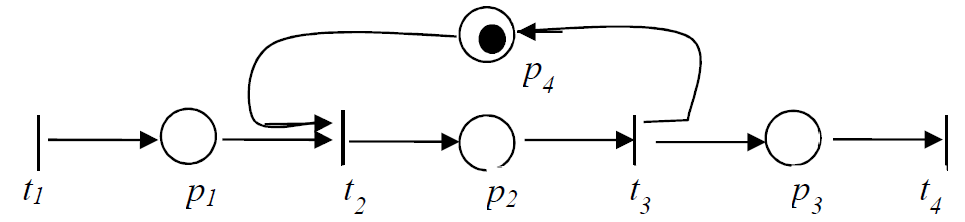
t1- поступила заявка на обработку; p1- задание ждет освобождения станции;
t2- задание начинает обрабатываться ; p2- задание обрабатывается ;
t3- конец обработки задания ; p3- задание ожидает очереди на выход ;
t4- передача выполненной заявки ; p4- рабочая станция свободна ;
Позиция p4 показывает, свободна ли рабочая станция. Наличие метки в позиции указывает на то, что станция свободна. Как только задание начинает обрабатываться, срабатывает переход t2, и маркировка позиции обнуляется. После окончания обработки запускается переход t3 и позиция p4 вновь получает метку. Таким образом, пока не сработает переход t3, новая заявка не может быть обработана.
Требуется описать с помощью сети Петри функционирование системы из предприятий A, В и С. Предприятия А и В поставляют узлы Х1 и X2 соответственно, а на предприятии С происходитсборка, в каждый сборочный узел входит один узел X1 и два узла X2. На рис. 2.10 предприятиям А, В и С соответствуют переходы t1, t2 и t3.
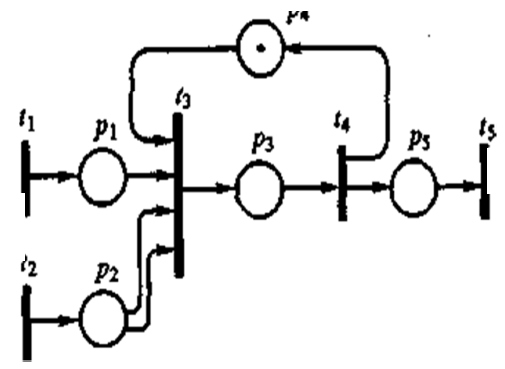
Срабатывание перехода t3 происходит только в том случае, если, во-первых, в позиции pl имеется метка, а в позиции р2 - не менее двух меток, что означает поступление от предприятия А и В соответствующих комплектующих, и, во-вторых, имеется метка в позиции p4, что означает, что предприятие С закончило сборку предыдущего изделия и готово приступить к сборке следующего. Пока очередное изделие не будет собрано, метки в p4 не будет, следовательно, запросы, пришедшие во входные позиции р1 и р2, вынуждены ожидать срабатывания перехода t4. Переходам t1, t2 и t3 поставлены в соответствие процедуры вычисления задержек срабатывания. Задержки в первых двух переходах равны интервалам времени между появлениями готовых узлов, задержка в t3 равна времени сборки изделия.
В практике моделирования объектов часто приходится решать задачи, связанные с формализованным описанием и анализом причинно- следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов. Самым распространенным в настоящее время формализмом, описывающим структуру и взаимодействие параллельных систем и процессов, являются сети Петри (англ. PetriNets), предложенные К. Петри.
Основные соотношения.Теория сетей Петри развивается в нескольких направлениях: разработка математических основ, структурная теория сетей, различные приложения (параллельное программирование, дискретные динамические системы и т. д.).
Формально сеть Петри (N-схема) задается четверкой вида N=,