Файл: правильные и полуправильные многогранники по дисциплине Математика.docx
Добавлен: 23.11.2023
Просмотров: 422
Скачиваний: 18
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В полуправильных многогранниках равны одноименные многоугольники; причем в каждой вершине сходится одно и тоже число одинаковых граней; в одинаковом порядке каждый из этих многогранников может быть вписан в сферу.
Конечно, возникает вопрос: сколько всего существует полуправильных многогранников? Более двух тысяч лет думали, что только тринадцать (их называют телами Архимеда, т.к. именно ему принадлежит их открытие), не считая двух бесконечных серий, составленных из призм и антипризм.
Но в настоящее время находят все новые и новые полуправильные многогранники. Так математик В.Г. Ашкинузе нашел еще один полуправильный многогранник. Если в многограннике ромбокубооктаэдр верхнюю «восьмиугольную чашу» повернуть на 45º, то получим многогранник, который «не совсем архимедово» тело: он не обладает некоторыми свойствами, которыми обладают тела Архимеда, но зато у него есть свои свойства. Кроме этого, можно еще представить полуправильные многогранники.
3.1. Тела Архимеда.
Многогранники, у которых все многогранные углы равны, а грани - правильные, но разноименные правильные многоугольники.
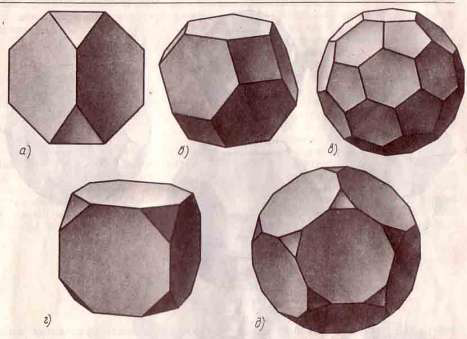
Многогранники такого типа называются равноугольно полуправильными многогранниками. Первую группу составляют пять многогранников, которые получаются из пяти платоновых тел в результате их усечения.
Вторую группу составляют два тела, называемых квазиправильными многогранниками. Это название означает, что гранями этого многогранника являются правильные многоугольники всего двух типов, причем каждая грань одного типа окружена гранями другого типа. Эти два тела называются: кубооктаэдр и икосододекаэдр. (приложение 1).
3.2 Тела Кеплера-Пуансо.
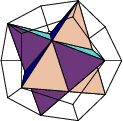Два тетраэдра, прошедших один сквозь другой, образуют восьмигранник. Иоганн Кеплер присвоил этой фигуре имя «стелла октангула» -«восьмиугольная звезда».Она встречается и в природе: это так называемый двойной кристалл. Такие тела получаются «озвездыванием» Платонова тела, то есть продлением его граней до пересечения друг с другом, и потому называются звездчатыми. Куб и тетраэдр не порождают новых фигур - грани их, сколько ни продолжай, не пересекаются. Эти многогранники ( приложение 2 ) из-за их необычных свойств симметрии исследуются с древнейших времѐн.
Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр. Пуансо открыл два других правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр.3.3. Тела Федорова.
Федоров Евграф Степанович (22.12.1853 –
21.05.1919) - русский кристаллограф, один из
основоположников структурной кристаллографии и
минерологи, геометр, петрограф и геолог, стал
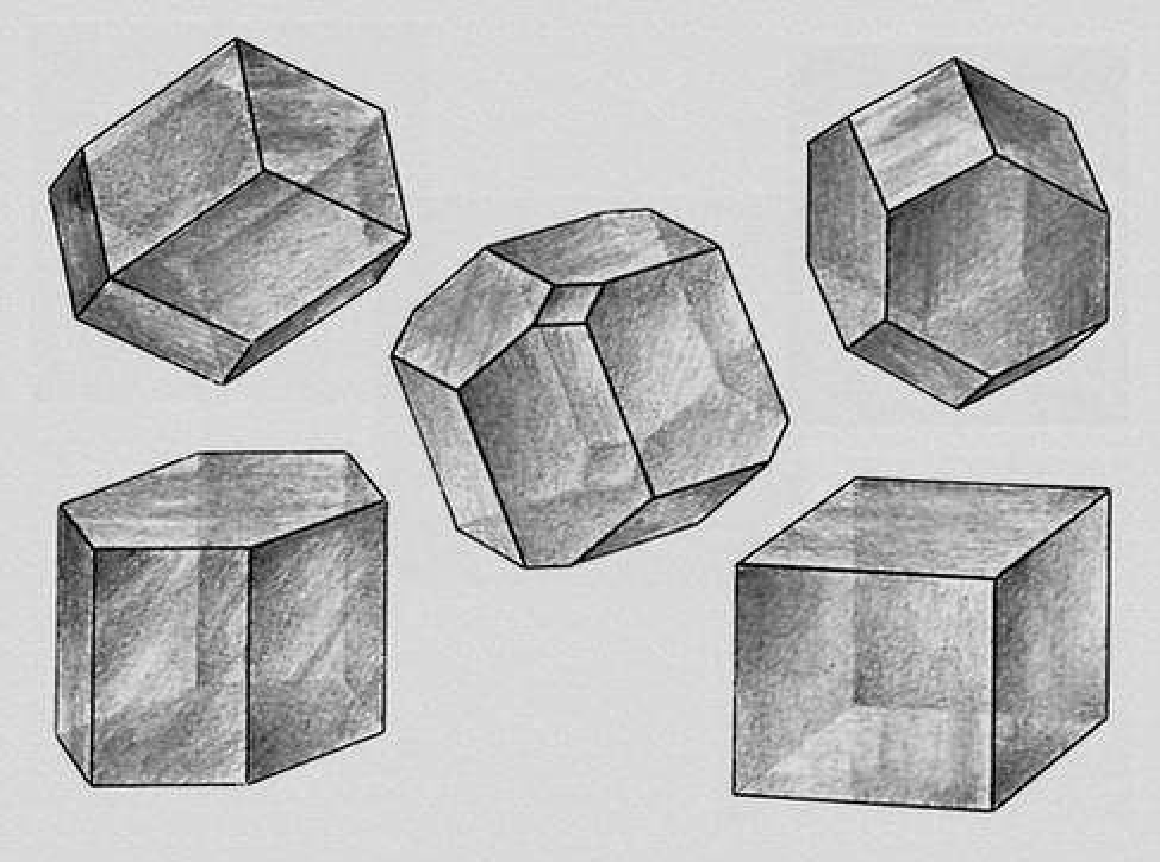
основоположником теории строения кристаллов. Его тела это выпуклые многогранники (параллелоэдры), параллельными переносами которых можно заполнить пространство так, чтобы они не входили друг в друга и не оставляли пустот между собой (т.е. являются параллелоэдрами). Существует 5 типов Федоровых тел, найденных им в 1881г.
3.4. Каталановы телаАрхимедовы тела являются полуправильными многогранниками в том смысле, что их грани - правильные многоугольники, но они не одинаковы, а каталановы - в том смысле, что их грани одинаковы, но не являются правильными многоугольниками; при этом для тех и других сохраняется условие пространственной симметрии.
4. Биография Платона.
(428 или 427до н. э., —347 до н. э.,) —древнегреческий философ, ученик Сократа, учитель Аристотеля. Настоящее имя — Аристокл. Платон — прозвище, означающее «широкий, широкоплечий».
Платон родился в семье, имевшей аристократическое происхождение. Первым учителем Платона был Кратил. Около 407 года познакомился с Сократом и стал одним из его учеников.
После смерти Сократа в 399 до н.э. уехал в Мегару.
В 389 году отправился в Южную Италию и Сицилию, где общался с пифагорейцами.
В 387 году Платон возвращается в Афины, где сновывает собственную школу — Платоновскую Академию. По древним преданиям Платон умер в
день своего рождения в 347 году. По свидетельству
Олимпиодора, Платон был не только философом, но и олимпийским чемпионом. Дважды он выигрывал соревнования по панкратиону — смесь бокса и борьбы.
4.1 Деятельность в цитатах.
Космос. Об отношении идеи к вещам.
«Мир — это не просто телесный космос, в нем общее совмещено с единичным, а космическое — с человеческим». Идеи — основа всего мира.
Политико-правовое учение Платона.
Основными политическими произведениями Платона являются трактаты «Государство», «Законы» и диалог «Политик».
Человек.
"Человек существо бескрылое, двуногое, с плоскими ногтями, восприимчивое к знанию, основанному на рассуждениях".
Математика.
Правильные многогранники или тела Платона Платону принадлежит разработка некоторых важных методологических проблем математического познания: аксиоматическое построение математики, исследование отношений между математическими методами и диалектикой, анализ основных форм математического знания.
4.2. Философия Платона
Великий древнегреческий ученый и его ученики в своих работах уделяли большое внимание правильным многогранникам, и их поэтому еще называют «платоновыми телами». Они считали, что эти тела олицетворяют сущность природы. Человечеству были известны четыре стихии: огонь, вода, земля и воздух. По мнению Платона их атомы имели вид правильных многогранников: огня — тетраэдр, земли — гексаэдр, воздуха —октаэдр, воды — икосаэдр. Но оставался еще додекаэдр, для которого отсутствует полное соответствие. Платон предположил, что существует еще одна сущность- мировой эфир, атомы которого имеют вид додекаэдра.
Огонь – наиболее подвижная стихия, он обладает разрушительным действием, проникая в другие тела (сжигая или расплавляя, или испаряя их); при соприкосновении с ним мы испытываем чувство боли, как если бы мы укололись или порезались. Какие частицы могли бы обусловить все эти свойства и действия? Очевидно, наиболее подвижные и легкие частицы, и притом обладающие режущими гранями и колющими углами. Из четырех многогранников, о которых может идти речь, в наибольшей степени удовлетворяет тетраэдр. Поэтому, говорит Платон, образ пирамиды (т.е. тетраэдра) и должен быть в согласии с правильным рассуждением и с правдоподобием, первоначалом и семенем огня. Наоборот, земля выступает как самая неподвижная и устойчивая из всех стихий. Поэтому частицы, из которых она состоит, должны иметь самые устойчивые основания. Из всех четырех тел этим свойством в максимальной мере обладает куб. Аналогичным образом с двумя прочими стихиями мы соотнесем частицы, обладающие промежуточными свойствами. Икосаэдр, как самый обтекаемый, представляет частичку воды, октаэдр – частицу воздуха.
Пятый многогранник – додекаэдр – воплощал в себе «все сущее», символизировал весь мир и почитался главнейшим.
ПРОНИКНОВЕНИЕ ПРАВИЛЬНЫХ И ПОЛУПРАВИЛЬНЫХ МНОГОГРАННИКОВ В ОКРУЖАЮЩИЙ МИР
1.Теория Кеплера
-
Кеплер Иоганн (Kepler I,1571-1630г) – немецкий астроном. Открыл законы движения планет. В 1596 году Кеплер предложил правило, по которому вокруг сферы Земли описывается додекаэдр, а в нее вписывается икосаэдр. ( «Гармония мира» 1619г.) -
И.Кеплер предположил, что расстояния между орбитами планет можно получить на основании Платоновых тел, вложенных друг в друга. Результаты его расчётов хорошо согласовались с действительными расстояниями между планетными орбитами -
Гипотеза Кеплера, в которой он попытался связать некоторые свойства Солнечной системы со свойствами правильных многогранников. Кеплер предположил, что расстояния между шестью известными тогда планетами выражаются через размеры пяти правильных выпуклых многогранников (Платоновых тел). Между каждой парой "небесных сфер", по которым, согласно этой гипотезе, вращаются планеты, Кеплер вписал одно из Платоновых тел. Вокруг сферы Меркурия, ближайшей к Солнцу планеты, описан октаэдр. Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы – додекаэдр( приложение 3). -
Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна. -
Эта модель выглядела для своего времени довольно правдоподобно. Во-первых, расстояния, вычисленные при помощи этой модели, были достаточно близки к истинным (учитывая доступную тогда точность измерения). Во-вторых, модель Кеплера давала объяснение, почему существует только шесть (именно столько было тогда известно) планет - именно шесть планет гармонировали с пятью Платоновыми телами. -
Однако даже на тот момент эта привлекательная модель имела один существенный недостаток: сам же Кеплер показал, что планеты вращаются вокруг Солнца не по окружностям ("сферам"), а по эллипсам (первый закон Кеплера). Нечего и говорить, что позже, с открытием еще трех планет и более точным измерением расстояний, эта гипотеза была полностью отвергнута. -
Замечено, что наша матушка-Земля последовательно проходит эволюцию правильных объемных фигур. Существует много данных о сравнении структур и процессов Земли с вышеуказанными фигурами. -
Полагают, что четырем геологическим эрам Земли соответствуют четыре силовых каркаса правильных Платоновских тел: Протозоа - тетраэдр (четыре плиты) Палеозою - гексаэдр (шесть плит) Мезозою - октаэдр (восемь плит) Кайнозою - додекаэдр (двенадцать плит).
2.Многогранники в искусстве
Большой интерес к формам правильных многогранников проявляли также скульпторы, архитекторы, художники. Их поражало совершенство, гармония многогранников. Леонардо да Винчи (1552-1519) увлекался теорией многогранников и часто изображал их на своих полотнах. Он любил изготовлять из дерева каркасы правильных многогранников и преподносить их в виде подарка различным знаменитостям. Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер (1471- 1528), в известной гравюре «Меланхолия» на переднем плане изобразил додекаэдр.
Сальвадор Дали на картине «Тайная вечеря» изобразил И.Христа со своими учениками на фоне огромного прозрачного додекаэдра.
Ярчайшим примером художественного изображения многогранников в XX веке являются, конечно, графические фантазии М.К. Эшера (1898-1972), голландского художника, родившегося в Леувардене. На гравюре "Четыре тела" Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.
Большое количество различных многогранников может быть получено объединением правильных многогранников, а также превращением многогранника в звезду. Изящный пример звездчатого додекаэдра можно найти в работе "Порядок и хаос". В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором.
Применения икосаэдров:
Титульный лист книги Ж. Кузена «Книга о перспективе».
Надгробный памятник в кафедральном соборе Солсбери.
Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц. Пирамида Хуфу, самая дальняя на рисунке, является самой большой. Пирамида его сына находится в середине и смотрится выше, потому что стоит на более высоком месте.
В III веке до н.э. был построен маяк, чтобы корабли могли благополучно миновать рифы на пути в александрийскую бухту. Ночью им помогало в этом отражение языков пламени, а днем - столб дыма. Это был первый в мире маяк, и простоял он 1500 лет.