Файл: правильные и полуправильные многогранники по дисциплине Математика.docx
Добавлен: 23.11.2023
Просмотров: 423
Скачиваний: 18
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Наш мир исполнен симметрии. С древнейших времен с ней связаны наши представления о красоте. Наверное, этим объясняется непреходящий интерес человека к правильным многогранникам - удивительным символам симметрии, привлекавшим внимание множества выдающихся мыслителей, от Платона и Евклида до Эйлера и Коши.
В моих приложениях (приложение 4) можно увидеть некоторые культурные ценности на которых изображены правильные многогранники.
-
(Сальвадор Дали. Тайная вечеря (1955)) -
Морис Эшер. “Рептилии”(литография, 1943 г). -
Надгробный памятник в кафедральном соборе Солсбери -
Титульный лист книги Ж. Кузена «Книга о перспективе»
3. Многогранники в природе
Правильные многогранники – самые выгодные фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов. Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она хорошо растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (NaCl) имеют форму куба.

-
При производстве алюминия пользуются алюминиево-калиевыми квасцами (K[Al(SO4)2]·12H2O), монокристалл которых имеет форму правильного октаэдра.

-
Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра (см.рис.).

-
В разных химических реакциях применяется сурьменистый сернокислый натрий (Na5(SbO4(SO4)) – вещество, синтезированное учеными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.

-
Последний правильный многогранник – икосаэдр передает форму кристаллов бора (B). В свое время бор использовался для создания полупроводников первого поколения.
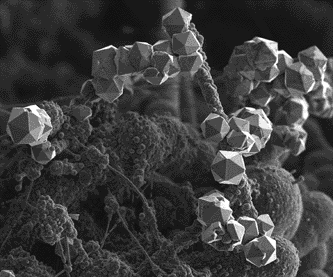
-
Итак, благодаря правильным многогранникам, открываются не только удивительные свойства геометрических фигур, но и пути познания природной гармонии.
На микроскопическом уровне, додекаэдр и икосаэдр являются относительными параметрами ДНК, по которым построена вся жизнь. Можно увидеть также, что молекула ДНК представляет собой вращающийся куб. При повороте куба последовательно на 72 градуса по определённой модели, получается икосаэдр, который, в свою очередь, составляет пару додекаэдру. Таким образом, двойная нить спирали ДНК построена по принципу двухстороннего соответствия : за икосаэдром следует додекаэдр, затем опять икосаэдр, и так далее. Это вращение через куб создаёт молекулу ДНК.
Вирусы, построенные только из нуклеиновой кислоты и белка, могут походить на жесткую палочкообразную или гибкую нитевидную спираль, точнее на правильный двадцатигранник, или икосаэдр. Есть вирусы, размножающиеся в клетках животных (позвоночных и беспозвоночных), другие облюбова-ли растения, третьи (их называют бактериофагами или просто фагами) паразитируют в микробах, но икосаэдрическая форма вирусов сохраняется во всех трех типах вирусов.
Математики говорили, что пчелы строили шестиугольные соты задолго до появления человека. Почему пчелы строят соты именно так?
Пчелы – удивительные создания. Если разрезать пчелиные соты плоскостью, то станет видна сеть равных друг другу правильных шестиугольников. Из правильных многоугольников с одинаковой площадью наименьший периметр именно у правильных шестиугольниковСтало быть, мудрые пчелы экономят воск (≈2% ) и время для постройки сот. На рисунке 1 изображена пчелиная ячейка в общем виде. На рисунке 2 можно увидеть, как соприкасаются ячейки в улье: их общая часть является ромбом.
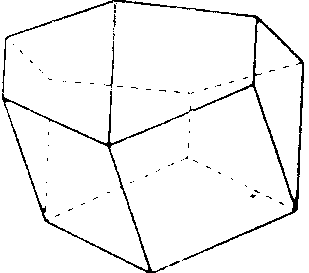
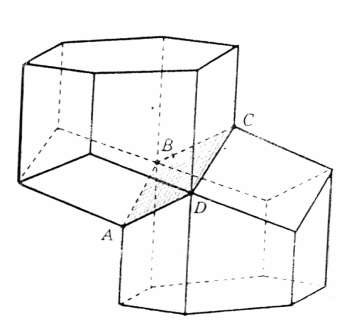
Рис. 1 Рис. 2
4. Мифические существа - духи.
Народное творчество, фантазия средневековых алхимиков и воображение поэтов населили 4 земные стихии мифическими существами – духами (приложение 5):
-
воздуха (октаэдр) – эльфы, -
земли (куб) – гномы, тролли, -
огня (тетраэдр) – саламандры, фениксы, -
воды (икосаэдр) – русалки, водяные. -
Духи земли - подземные человечки - гномы, или кобольды, помогали людям находить -
подземные богатства; -
Духи воды – златокудрые русалки, или ундины, с рыбьим хвостом вместо ног, пели
вечерами обворожительные песни;
Духи огня – пляшущие в огне человечки в виде ящериц – саламандры.
-
Светлые эльфы в средневековой демонологии духи воздуха, — красивые, маленькие человечки (ростом с дюйм) в шапочках из цветков, беззаботно кружились в своем вечном танце.
5. Планета Земля и многогранники.
Идеи Платона и Кеплера о связи правильных многогранников с гармоничным устройством мира и в наше время нашли своё продолжение в интересной научной гипотезе, по которой считается, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. «Лучи» этого кристалла, а точнее, его силовое поле, обуславливают икосаэдро-додекаэдровую структуру Земли. Она проявляется в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. 62 вершины и середины ребер многогранников, называемых авторами узлами
, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления. Если нанести на глобус очаги наиболее крупных и примечательных культур и цивилизаций Древнего мира, можно заметить закономерность в их расположении относительно географических полюсов и экватора планеты. Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки (приложение 6). Еще более удивительные вещи происходят в местах пересечения этих ребер: тут располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник. Московские инженеры В.Макаров и В.Морозов потратили десятилетия на исследование данного вопроса. Их теория утверждает, что ядро Земли представляет собой растущий кристалл железа, который наводит во всех оболочках планеты симметрию двух правильных платоновых многогранников - икосаэдра и додекаэдра, а также иерархию подсистем основного деления, - поэтому такая система получила название икосаэдро-додекаэдрической структуры Земли, то есть ИДСЗ, а за рубежом .
ЗАКЛЮЧЕНИЕ.
В огромном саду геометрии каждый
найдет букет себе по вкусу.
Д.Гильберт (1862-1943) -
немецкий математик.
Работая над рефератом «Правильные и полуправильные многогранники» мной были предприняты следующие действия:
- изучены информационные источники, имеющие отношение к истории возникновения и развития понятия симметрии (см. список информационных источников),
- уточнены и дополнены теоретические аспекты данного понятия,
- установлена значимость и проникновение правильных многогранников в определенные области знания.
Следует отметить, что изучая информационные источники:
- я столкнулась с разнообразными видами правильных и полуправильных многогранников,
мне пришлось окунуться в мир многообразия новых для меня терминов, а так же понять, что собранные мной сведения выходят за рамки школьного курса геометрии,
- выяснила, что правильные многогранники удивительным образом связаны с мифологическими существами.
Таким образом, учитывая все законы пространства и изучив различные типы правильных многогранников можно сделать вывод, что самое прекрасное и совершенное приходит к нам от природы.
СПИСОК ЛИТЕРАТУРЫ.
1. Атанасян, В.Ф. Бутузов, С.Б. Кардомцев и др.–5-е изд.– М.:Просвещение, 1997.
2. Лаптев Б.Л.. Н.И.Лобачевский и его геометрия. М.: Просвещение,1976.
3. Фридман Л.М., Изучаем математику, Москва, «Просвещение», 1995г
4. Гарднер М. Математические новеллы. Пер. с англ. Ю.А.Данилова.М., «Мир», 1974.
5. Погорелов А.В. Геометрия. Учебное пособие для 7-11 классов. М.,Просвещение, 1992.
6. Тихонов А.Н., Костомаров Д.П.. Рассказы о прикладной математике.М.: Вита-Пресс, 1996
7. Гильберт Д., Кон-фоссен С. Наглядная геометрия. М.: Наука, 1981
ИНТЕРНЕТ-РЕСУРСЫ.
http://ru.wikipedia.org
http://www.krugosvet.ru
http://schools.techno.ru
http://genius.pstu.ru/file.php/1/pupils_works_2012/Alikina_Alla.pdf