Файл: Задача 1 Расчёт идеального компрессора.docx

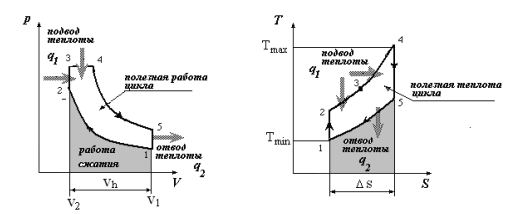
Задача №1Расчёт идеального компрессора.В одноступенчатом идеальном компрессоре сжимается идеальный газ, имеющий начальное избыточное давление р_1ман , кПа, температуру t₁, ⁰С и подается потребителю в количестве М, кг/с (массовый расход) под избыточным давлением р_2ман. Определить температуру газа в конце сжатия, плотность в начале и в конце сжатия при изотермическом, адиабатическом и политропном (показатель политропы n) процессах сжатия. Сравнить теоретические мощности, затрачиваемые на привод компрессора; количество выделяемой теплоты в каждом из указанных процессов сжатия. 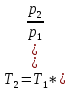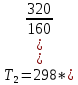Изобразить процессы сжатия в p-v и T-∆s координатах с учетом масштаба.Дано:Т₁= 298 Кр_1ман= 60 КПар₁= 60+100=160 КПаn = 1,8газ Кислород О₂k = 1,4R_О2 = 259,8 Дж/кг*КM = 0,25 кг/ср_2ман= 220 КПар₂=220+100=320 КПаРешение:1) Определение термических параметров состояния в характерных точках рабочего цикла компрессора1.1) Абсолютная температура газа после сжатия Адиабатический процесс:Политропный процесс: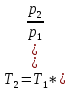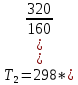Изотермический процесс: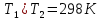1.2) Плотность газаВ начале сжатия: 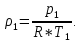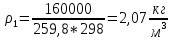В конце адиабатического сжатия: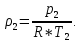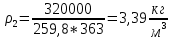В конце политропного сжатия: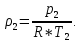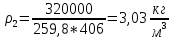В конце изотермического сжатия: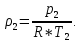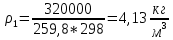2) Определение энергетических параметров работы компрессора

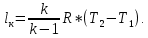
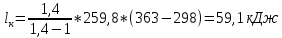
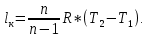
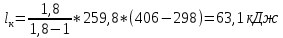
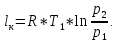
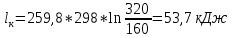
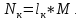
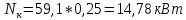
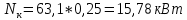
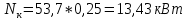
2.1) Определение удельных затрат механической энергии (работы) на привод компрессораПри адиабатическом сжатии:При политропном сжатии:При изотермическом сжатии:2.2) Определение теоретической мощности привода компрессора:Для адиабатического сжатия:Для политропного сжатия:Для изотермического сжатия:3) Определение теплоты, отводимой от газа в процессе сжатия3.1) Удельная теплота для изотермического процесса: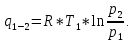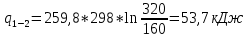3.2) Вся теплота с учетом массового расхода для изотермического процесса: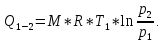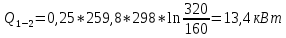3.3) Удельная теплота для политропного процесса: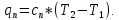где c_n- удельная массовая теплоемкость политропного процесса: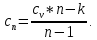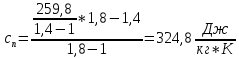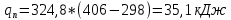3.4) Вся теплота с учетом массового расхода для политропного процесса:

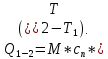
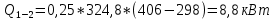
Вид процесса сжатия	Абсолютная температура в конце сжатия, К	Плотность газа до сжатия, кг/м³	Плотность газа после сжатия, кг/м³	Теоретическая мощность привода, кВт	Количество отводимой теплоты, кВт
Газ			Кислород (О₂)
Адиабатический	363		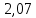		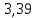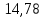0
Политропный	406		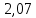		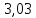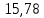8,8
Изотермический	298		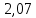		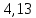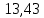13,4

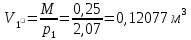
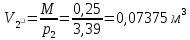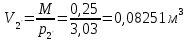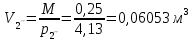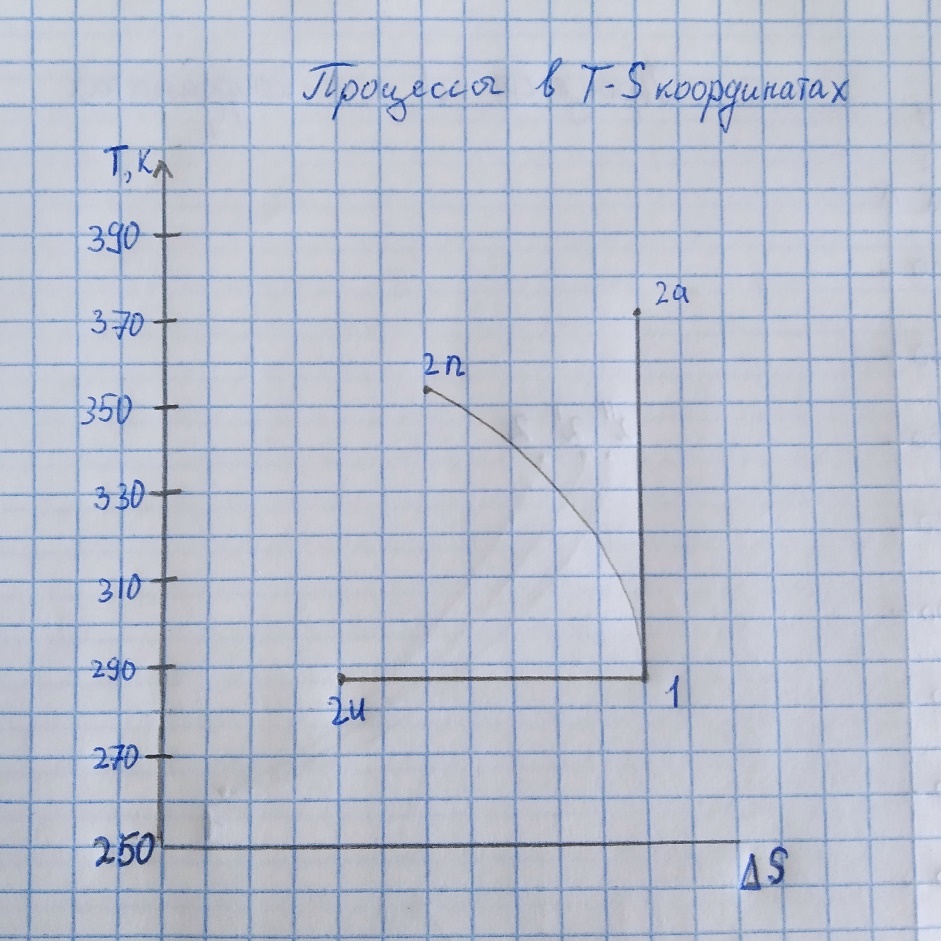
Таблица 1 - Результаты расчета (адиабатическое сжатие) (политропное сжатие) (изотерическое сжатие)1 – начало процесса, 2и – конец изотермического процесса, 2а – конец адиабатического процесса, 2п – конец политропного процессаВыводы:

Расчет параметров процесса сжатия водорода в компрессоре показал, что с ростом показателя политропы (от 1 до 1,9) увеличиваются такие характеристики как конечная температура, мощность привода, все максимальные значения получены для политропного процесса при n=1,3<1,4.
Плотность газа в конце процесса, напротив, убывает с ростом показателя политропы (максимальное значение в конце изотермического процесса 2,57 кг/м³и минимальное в конце политропного 1,46 кг/м³)

Задача №2Расчёт идеального прямого термодинамического цикла. Для идеального термодинамического цикла теплового двигателя определить параметры состояния рабочего тела в характерных точках, удельную работу расширения каждого процесса (для 1 кг рабочего тела), изменение внутренней энергии и энтальпии каждого процесса, термический КПД цикла, среднее давление цикла, удельную теоретическую литровую (для 1 л рабочего объема) мощность двигателя. Рабочее тело - идеальный газ со свойствами воздуха (R=287 Дж/(кг.К), k=1,4). Известны параметры в начальной точке: абсолютное давление p₁кПа и температура t₁=10˚С, а также степень сжатия ε=11, количество подводимой теплоты на изохорном участке цикла q_v₌₀, количество подводимой теплоты на изобарном участке q_р=1,4МДж/кг, частота вращения коленчатого вала n=5600 мин^-1. Изобразить цикл в координатных системах «p-v» и «T-∆s» с учетом масштаба.

Рисунок 2 – Схема идеального цикла Тринклера

Исходные данные:

ε=11;q_v=0.7МДж/кг; q_р=0.8МДж/кг;n=2000мин^-1;к=1.4

t₁=10С=283К; р₁=99кПа; R=287Дж/кгК

Найти: Т_1-5, Р_1-5, V_1-5, q_1-5, l_1-5, ΔU_1-5, ΔS_1-5, ΔH_1-5, P_t, H_t, N_t

Расчет идеального цикла Тринклера

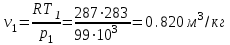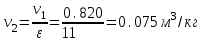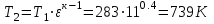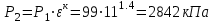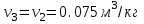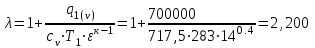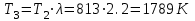
Процесс 1-2 (адиабата): . . . .Процесс 2-3 (изохора): . . .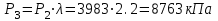Процесс 3-4 (изобара): 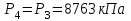. .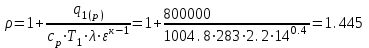 . .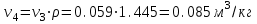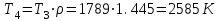Процесс 4-5 (адиабата):

.

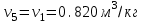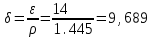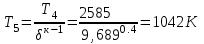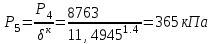Таблица 2 – Результаты расчета

Вид цикла – Тринклера, ε=14, λ=2,200, ρ=1,445
Характерные точки процессов цикла	Абсолютное давление, МПа	Абсолютная температура, К	Удельный объём, м³/кг
1	0,099	283	0,820
2	3,983	813	0,059
3	8,763	1789	0,059
4	8,763	2585	0,085
5	0,365	1042	0,820

Расчет энергетических характеристикПроцесс 1-2 (сжатие): 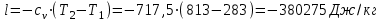. .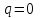 . .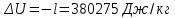 .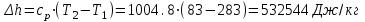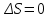Процесс 2-3 (подвод теплоты по изохоре): 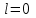. .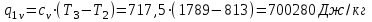 . .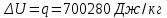 .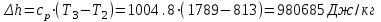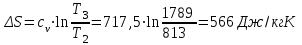Процесс 3-4 (подвод теплоты по изобаре): 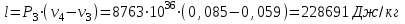. .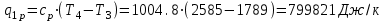 . .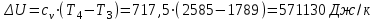 .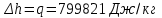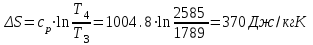Процесс 4-5 (расширение): 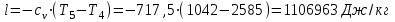. .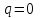 . .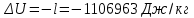 .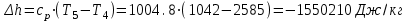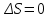Процесс 5-1 (отвод теплоты): 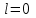. .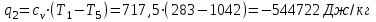 . .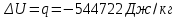 .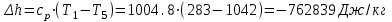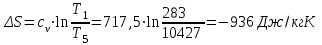Таблица 3 – Результаты расчетов

Вид цикла – Тринклер, ε=14, λ=2,200, ρ=1,445
Процесс	Уд. Теплота кДж/кг	Уд. Работа, кДж/кг	Изменение уд. Внутр. Энергии, кДж/кг	Изменение уд. Энтальпии, Дж/кг	Проверка выполнения q=ΔU+l
1-2	0	-380,275	380,275	0	380,275-380,275=0
2-3	700,280	0	700,280	566	0+700,2=700,28
3-4	799,821	228,691	571,130	370	571,13+228,691=799,821
4-5	0	1106,963	-1106,963	0	1106,963-1106,963=0
5-6	-544,722	0	-544,722	-935	-544,722+0=-544,722
Проверка	955,379	955,379	0	0