Файл: Задача 1 Расчёт идеального компрессора.docx

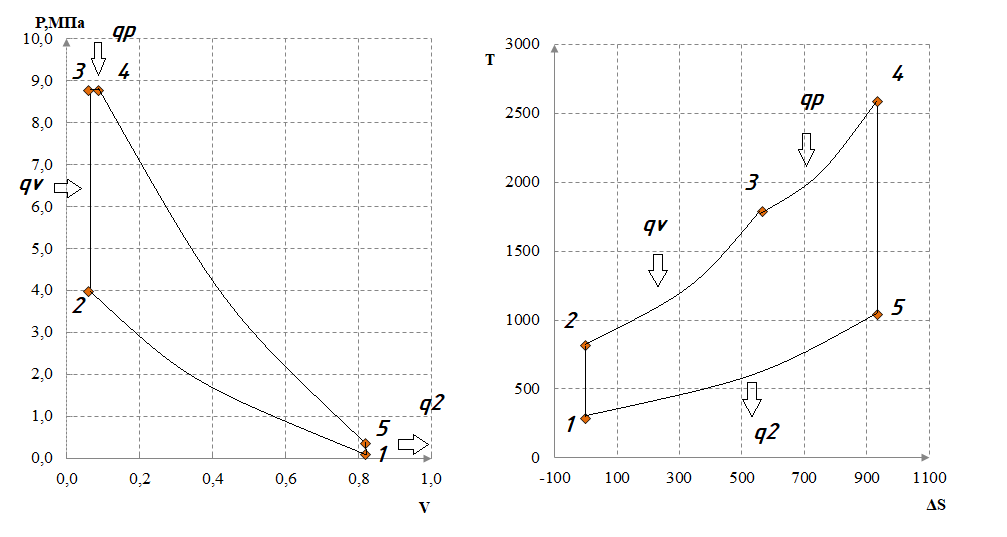
Рисунок 3 – Изображение цикла Тринклера согласно расчетов
Термический КПД:



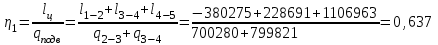
Среднее давление


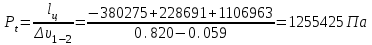
Теоретическая удельная литровая мощность двигателя:


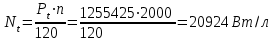
Выводы:

1. 
   Произведен расчет состояния рабочего тела (воздуха) в характерных точках цикла Тринклера (степень сжатия 14) - температура, давление, удельный объем.
   
2. 
   Произведен расчет энергетических характеристик – изменение удельной работы, теплоты, внутренней энергии, энтальпии и энтропии.
   
3. 
   Результаты расчетов отражены на графиках.
   
4. 
   Среднее давление цикла - 1,26МПа.
   
5. 
   Термический ЕПД 0,637.
   
6. 
   Теоретическая удельная литровая мощность равна 20,924 кВт/л.
   

Задача №3

Расчёт теплопередачи через плоскую стенку

Определить величину удельных тепловых потерь за счет конвекции ограждающей конструкции (стен) жилого здания, если на стене толщиной 1 с внутренней стороны имеется слой штукатурки (или дерева) толщиной 2 , под которым размещен слой тепловой изоляции толщиной 3. С наружной стороны стены имеется слои штукатурки такой же толщиной 2.

Известны: коэффициент теплопроводности материала стены 1, коэффициент теплопроводности материала слоя штукатурки или дерева 2, коэффициент теплопроводности слоя тепловой изоляции 3.

Внутри помещения требуется поддерживать температуру воздуха tf1; с наружной стороны стены установилась температура окружающего воздуха tf2.

Коэффициент теплоотдачи с внутренней стороны стены 1=8,7 Вт/(м2К), коэффициент теплоотдачи с внешней (уличной) стороны для зимних условий 2=23 Вт/(м2К) - соответствуют требованиям СНиП 23-02-2003 Свод правил. Тепловая защита зданий.

Рассчитать температуры поверхностей слоев стены. Построить графики изменения температуры по толщине многослойной стенки с учетом масштаба температуры и толщины.

Определить глубину промерзания стены для заданных условий (тепловая изоляция установлена на внутренней поверхности стены.

Дано :

α₁ = 8,7 Вт/(м²*К); α

---

₂ = 23 Вт/(м²*К).

Материал стены – Монолитный железобетон

δ₃ = 0,5 м; λ₃ = 1,55 Вт/(м*К);

δ₄ = 14 мм = 0,014м; λ₄= 0,44 Вт/(м*К);

Штукатурка;

Материал изоляции – Пенополистирол

δ₂ = 40 мм = 0,04 м; λ ₂= 0,064 Вт/(м*К);

λ ₁ =0,18 Вт/(м*К) δ₁ =0,018м( дерево сухая сосна)

t_{f 1}= 19°С; t_f2 = -30°С;

Решение:

1. 
   Термическое сопротивление теплопередачи через плоскую трёхслойную стенку:
   

2. 
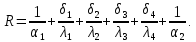
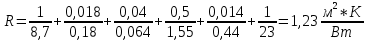
   Плотность теплового потока через плоскую четырехслойную стенку:
   

3. 
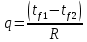
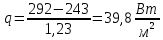
   Определение термического сопротивления и плотности теплового потока без изоляции:
   

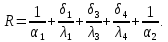
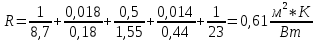
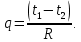
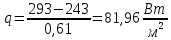
Тепловой поток без изоляции увеличится на 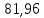-39,8=42,16 Вт/м²

4. 
   Температура внутренней и внешней поверхности многослойной стенки и на границе слоев:
   

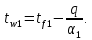
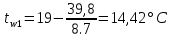
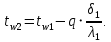
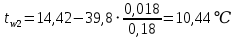
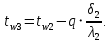
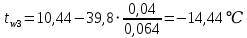
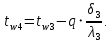
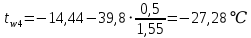
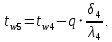
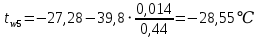
Проверка:





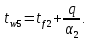
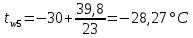
Определение глубины промерзания слоя пенополистирола:

---

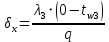
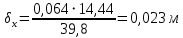
Глубина промерзания стены составит:

5. 
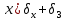
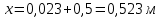
   Температура внутренней и внешней поверхности многослойной стенки и на границе слоев без изоляции:
   

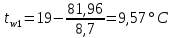
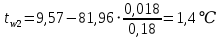
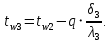
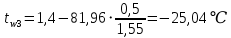
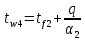
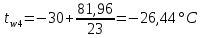
Определение глубины промерзания:





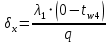
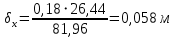
Глубина промерзания стены со штукатуркой (снаружи) составит:






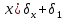
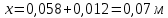
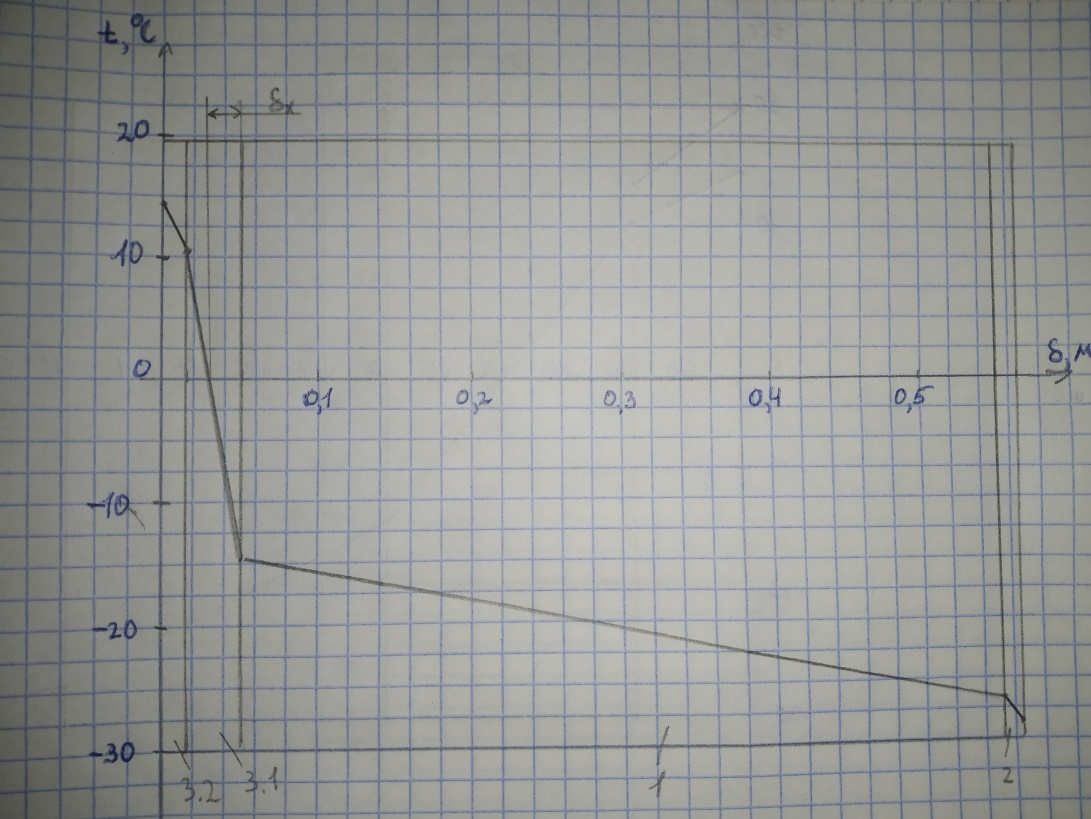
1 – Монолитный железобетон; 2 – штукатурка; 3.1 – пенополистирол; 3.2 – дерево (сухая сосна)

Рисунок 6 – Распределение температуры по толщине четырехслойной плоской стенки


Выводы:

1. 
   Удельные тепловые потери через стенку составляют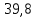 Вт/м².
   
2. 
   Рассчитаны температуры на границе слоев и на поверхностях стены. Построен график в масштабе.
   
3. 
   Глубина промерзания стены 0,523 м.
   

Задача 4

Расчёт теплопередачи через цилиндрическую стенку
Внутри трубы с внутренним диаметром d₁ и толщиной стенки δ₁, изготовленной из материала с коэффициентом теплопроводности λ₁, имеющей на внутренней поверхности слой накипи толщиной δ₀ с коэффициентом теплопроводности λ₀ , движется горячая вода со скоростью w₁, имеющая среднюю температуру t_f1.

Наружная поверхность покрыта слоем материала толщиной δ₂ с известным коэффициентом теплопроводности λ

---

₂ и находится в воздухе, имеющем температуру t_f2 при отсутствии вынужденного движения. Известна степень черноты наружной поверхности ε.

Определить:

1 Линейную плотность теплового потока (тепловые потери с 1 м длины), передаваемого в воздух с наружной поверхности за счет свободной конвекции.

2 Критический диаметр изоляции (внешнего слоя); сделать вывод об эффективности наружного слоя как тепловой изоляции.

3 Температуры: на поверхности накипи со стороны воды; на внутренней и наружной поверхности стенки трубы; на наружной поверхности внешнего слоя (изоляции). Построить график изменения температуры по толщине многослойной цилиндрической стенки для условий задачи в масштабе.

4 Линейную плотность теплового потока (тепловые потери с 1 м длины), передаваемого в воздух за счет излучения наружной поверхности трубы.


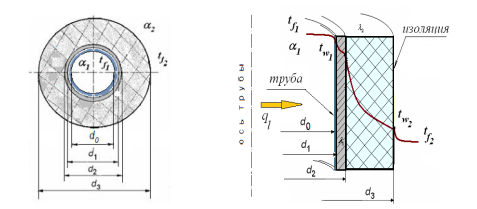
Рисунок 8 – Схема многослойной цилиндрической трубы

Дано:

Таблица 1 – Исходные данные

d1, мм	δ0, мм	δ1, мм	δ2, мм	λ0, Вт/мК	λ1 Вт/мК	λ2, Вт/мК	w1, м/с	tf1, ºС	tf2, ºС	ε
18	0,6	0,8	15	1,8	30	0,055	1,8	70	15	0,85

Материал трубы – Алюминиевый сплав, материал наружного покрытия трубы – Минер вата

Таблица 2 – Теплофизические свойства теплоносителей

№	Теплофизические свойства среды	Единицы измерения	Вода при средней температуре	Воздух при средней температуре
1	Коэффициент теплопроводности,	Вт/м*К	0,680	0,0263
2	Коэффициент кинематической вязкости, 106	м2/с	0,415	14,61
3	Число Прандтля (Pr) при средней температуре среды (tf)	-	2,55	0,704
4	Число Прандтля (Pr) при средней температуре стенки (tw)	-	2,98	0,702

---

Решение:

1. 
   Определение коэффициента теплоотдачи при вынужденном течении воды внутри трубы.
   

Критерий Рейнольдса:





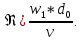
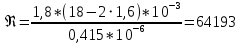
Критерий Нуссельта:





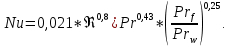
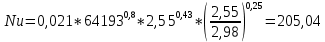
Коэффициент теплоотдачи при вынужденном течении воды внутри трубы:

2. 
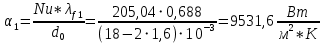
   Определение коэффициента теплоотдачи в воздух с внешней стороны трубы при свободной конвекции с изоляцией.
   

Критерий Грасгофа:





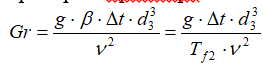
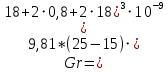
Критерий Нуссельта:





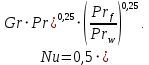
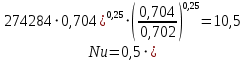
Коэффициент теплоотдачи в воздух с внешней стороны трубы при свободной конвекции:

3. 
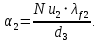
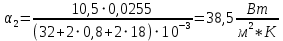
   Определение суммарного термического сопротивления и коэффициента теплопередачи.
   

Линейное термическое сопротивление внутри трубы:





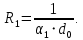
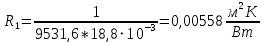
Линейное термическое сопротивление слоя накипи:





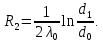
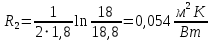
Линейное термическое сопротивление стенки трубы:





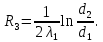
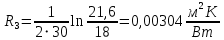
Линейное термическое сопротивление слоя изоляции:





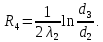
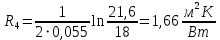
Линейное термическое сопротивление на границе:





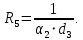
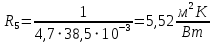
Суммарное линейное термическое сопротивление трубы:

---