Визуализация деревьев при помощи OpenGL в C++
Постановка задачи:

1. 
   Написать программу, которая будет рисовать бинарное дерево на подобии того, что показано на рис. 1:
   

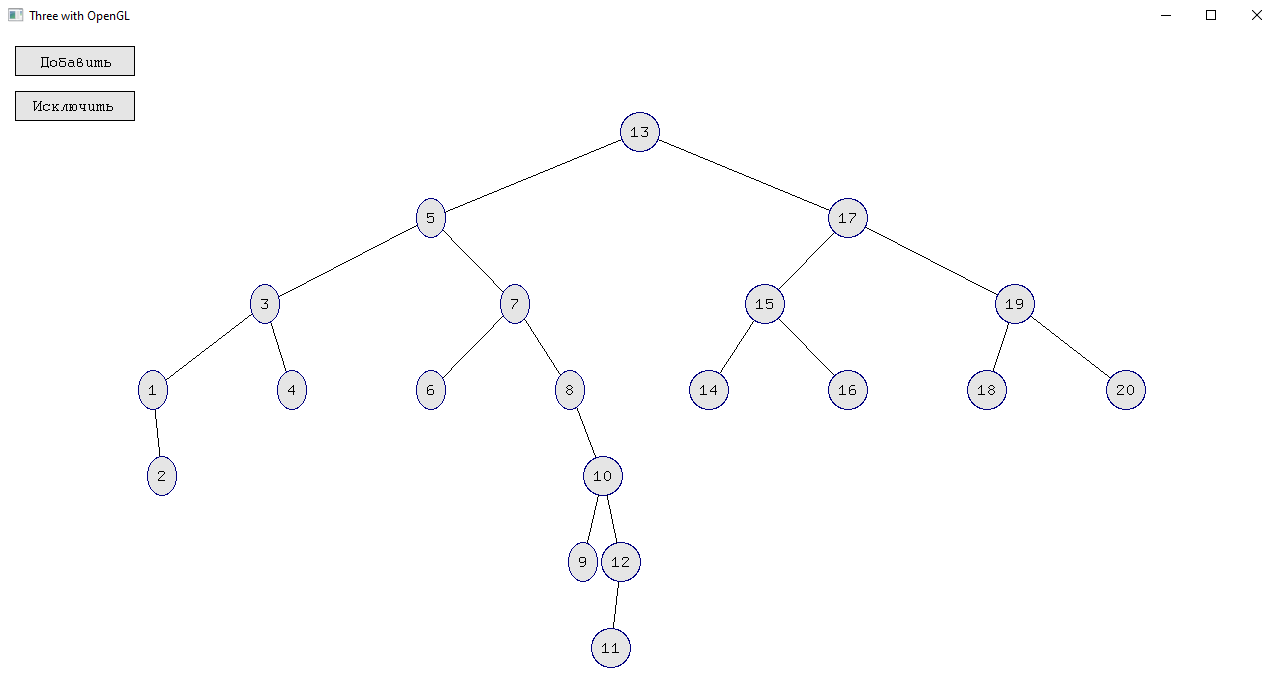
Рисунок 1 – Пример выполнения работы

2. 
   Программа должна содержать кнопки управления, которые будут позволять выполнять базовые операции и действия, указанные в вашем варианте Лабораторной работы №30 «АТД. Деревья»:
   

Рисунок 2 – Панель управления

3. 
   Для ввода можно использовать консоль:
   

Рисунок 3 – Ввод с консоли

4. 
   Кнопки и узлы дерева должны подсвечиваться при наведении на них курсора мыши. Это может быть смена фона, либо цвета и толщины границы элемента, либо комбинация перечисленного:
   

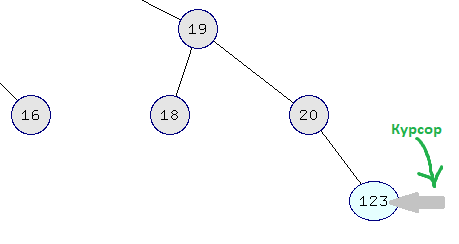
Рисунок 4 – Подсветка элементов

5. 
   При выполнении работы можно пользоваться:
   

• 
  Лекцией по OpenGL, выложенной на сайте;
  
• 
  Вспомогательными материалами, изложенными далее;
  
• 
  Лекциями по математике за 1 семестр (потребуется вычислить, содержится ли точка в области эллипса, например);
  
• 
  Книгой Дейва Шрайнера OpenGL Redbook, в которой вы найдете все ответы на оставшиеся вопросы (настоятельно рекомендуется).
  

Вспомогательные материалы

Переменные и прототипы функций

Для представления бинарного дерева в OpenGL необходимо знать координаты, каждого из элементов. Не случайно до этого была выведена формула вычисления координат каждого узла для функции вертикальной печати.

То, сколько пробелов нужно поставить перед данным элементом, отсчитывая с начала печатаемой в консоли строки, предназначенной для печати отдельного уровня дерева, зависит от уровня, на котором сейчас находится элемент, от уровня, который может быть в принципе в качестве максимального, и, естественно, от минимальной ширины дерева, требуемой для печати какого-либо полного дерева (если печатается неполное дерево, то оно пополнится значениями NULL). Ширина данных, хранимых в дереве, при печати может занимать более одного символа,

---

вследствие чего введен дополнительный коэффициент, выбираемый пользователем. И это очень удобно.

Можно считать, что это количество пробелов – эквивалент координаты х, а текущий уровень – это у. Следовательно, мы действительно имеем дело с координатами.

Но эти значения координат пока что не готовы к использованию в представлении дерева в OpenGL. Их нужно преобразовать в зависимости от ширины, высоты окна, возможного отступа (от краев окна), а так же от собственных характеристик дерева, как например, от введенной до этого понятия минимальной ширины печатаемого дерева и его высоты (будут использоваться некоторые понятия из функции вертикальной печати). Так, будущее дерево будет отображаться в некоторых рамках, то есть предусматриваем факт того, что пространство для изображения дерева ограничено. При этом будем стараться разместить дерево по максимуму в данном пространстве, соблюдая отступы, не нарушая границ окна. И распространяться дерево будет как в ширину, так и в высоту, но, в основном, размеры элементов будут зависеть от ширины.

Будут введены новые коэффициенты, которые помогут расширять дерево динамически. Имеется в виду, что, меняя факторы, от которых зависит рисунок дерева, будут меняться и координаты элементов, и размеры фигур, внутри которых будут размещены какие-либо данные. Кроме того, учтем то, что ширина данных может быть больше единицы.

Пусть такое дерево на рисунке 1 имеет высоту, равную 3, минимальную ширину (если бы мы его печатали), равную 7, и максимальную ширину данных - 3.
Ширина и высота окна, соответственно, 800 и 600, а отступ от краев 10.

При этом радиусы кругов (размещаться данные будут в кругах) таковы, что между любыми элементами можно расположить как минимум один такой же.


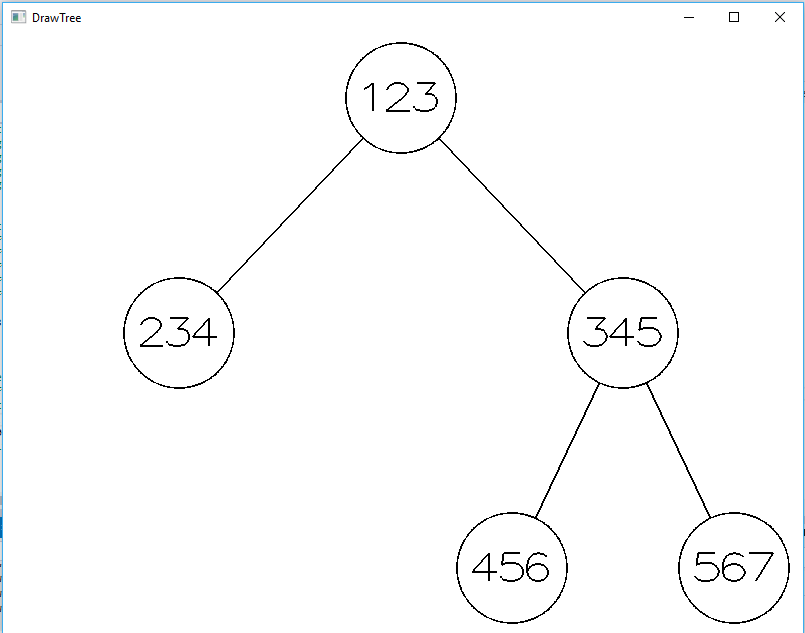
Рисунок 1 – изображение дерева в окне 800х600

Понадобится несколько аргументов, от которых в дальнейшем будет зависеть то, как дерево будет выглядеть на рисунке.

Кроме того, что в функцию отображения дерева придется занести само дерево, необходимо воспользоваться и знанием о ширине, высоте окна, величине отступа от краев окна (дабы дерево не находилось вплотную к его краям), а также знакомый нам из функции вертикальной печати коэффициент ширины данных. Вообще, у меня был еще коэффициент расширения дерева, преобразующий координаты элементов при вертикальной печати, таким же образом, что и КШД, но в данном случае использовать его бессмысленно, ведь он будет ухудшать видимость элементов (незачем еще раз масштабировать дерево, раз это приведет к дополнительным неудобствам даже для пользователя, желающего посмотреть на рисунок дерева).

---

На основании вышеизложенных аргументов нужно просчитать в первую очередь радиусы кругов элементов, затем в координаты самих элементов, а затем координаты текста.

Обозначения:

• 
  window_width – ширина окна;
  
• 
  window_height – высота окна;
  
• 
  tree_width – минимальная ширина дерева (МШД), используемая для вертикальной печати;
  
• 
  tree_height – высота дерева;
  
• 
  shift – отступ от краев (одинаковый с двух сторон);
  
• 
  R – радиус круга;
  
• 
  node_x – х-координата элемента;
  
• 
  node_y – y-координата элемента;
  
• 
  k_x – коэффициент пропорциональности по оси Ох;
  
• 
  k_y – коэффициент пропорциональности по оси Оy;
  
• 
  text_x – х-координата текста;
  
• 
  text_y – y-координата текста;
  
• 
  x – индекс узла на данном уровне, если представить уровень как массив;
  
• 
  у – текущий уровень;
  
• 
  k – коэффициент расширения данных.
  

Если элемент в дереве один (а это означает, что высота и МШД равны), то

(Формула 1)

Иначе

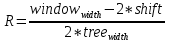.	(Формула 2)

Если элемент в дереве один, то

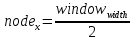,	(Формула 3)
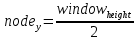,	(Формула 4)

иначе считаем коэффициенты пропорциональности по осям Ох и Оу, чтобы получить координаты:

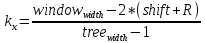,	(Формула 5)
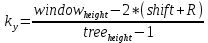,	(Формула 6)
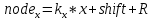,	(Формула 7)
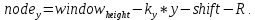	(Формула 8)
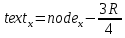,	(Формула 9)
.	(Формула 10)

---

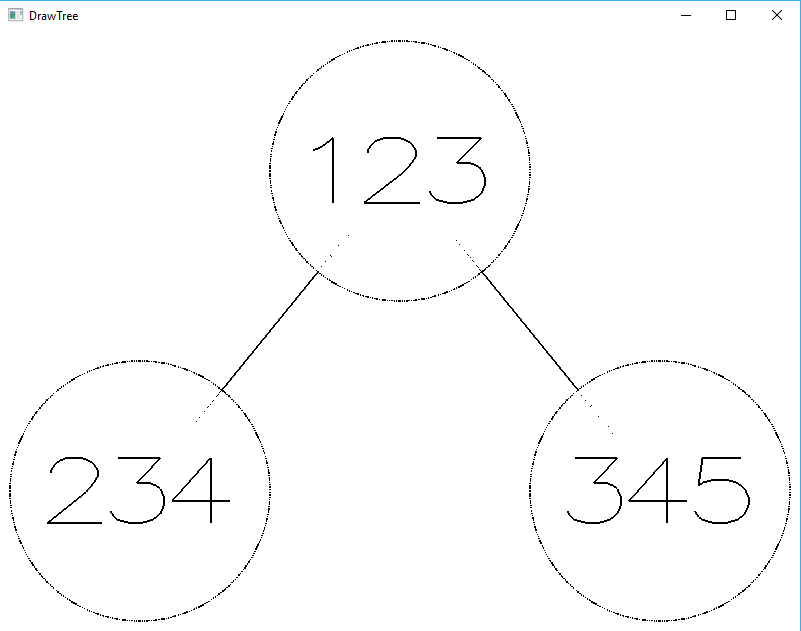
Главное свойство дерева, которое будет нарисовано – масштабируемость.
При этом меняются не только расстояние между элементами и размеры кругов, но и шрифт (необходимо заострить на этом внимание, так как в будущем на основании этого свойства будет рисоваться текст определенным шрифтом).

На рисунке 2 представлены деревья разных размеров в окошке одних и тех же размеров для показательности масштабирования.


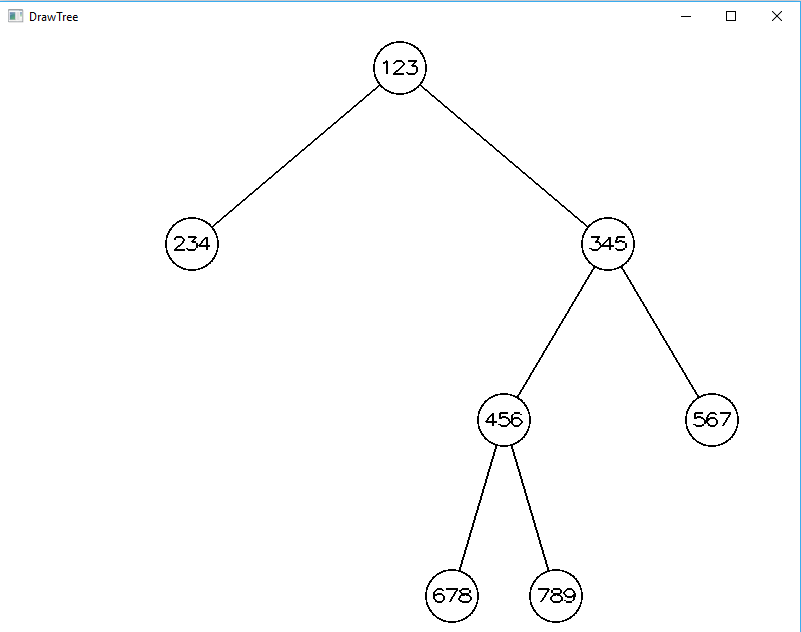Рисунок 2 – изображения разных деревьев в окне 800х600

Кроме того, при наведении курсора на элемент, цвет окружности поменяется на синий, что продемонстрирует работу с мышью (рисунок 3).


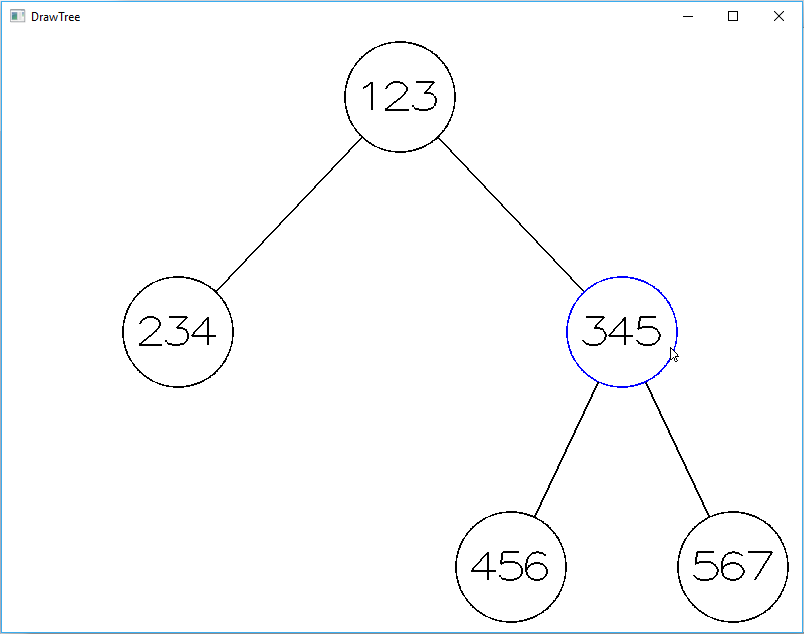
Рисунок 3 – изменение цвета окружности при наведении мыши

Так как некоторые актуальные функции OpenGL принимают только прописанные в них аргументы, что вызывает некоторые неудобства, придется воспользоваться глобальными переменными.

Ниже создается структура в заголовочном файле “tree.h”, в которой обозначены такие глобальные переменные, как tree – копия дерева, а также ширина, высота окна, отступ, коэффициент ширины данных, радиус круга, координаты чего-либо и переменная состояния, которая в будущем пригодится нам при работе с мышью:
struct SGlutContextStruct

{

void* tree;

int window_width, window_height, shift, k, R, x, y, state;

};

В классе Tree появятся новые поля и функции. Главная функция - drawTree():
int node_x;

int node_y;

int text_x;

int text_y;
//установить координаты для данного узла при рисовании

void setCoordsForNode(

int window_width, int window_height,

int shift,

int tree_width, int tree_height,

int x, int y, int R);
template

Tree* Tree::getNodeByCoords(int x, int y, int R);
//установить координаты для текста текущего узла при рисовании

void setCoordsForText(int k, int shift);
//рисовать дерево

void drawTree(

int argc, char** argv,

int window_width, int window_height,

int shift, int k);

Реализация функций

Подключается структура, позволяющая инициализировать переменные и выполнять с ними какие-либо операции в дальнейшем, в файле “tree.cpp” – он же файл описания классов Tree/SearchTreе:
extern SGlutContextStructglutContext;
Реализуются три первые новые функции, показанные до этого. Функции-сеттеры используют формулы, разработанные ранее, а функция-геттер, используя вспомогательную функцию, проходится по дереву и сверяется со стандартной формулой окружности в координатной плоскости хОу для того, чтобы найти узел.
template

void Tree::setCoordsForNode(

int window_width, int window_height,

int shift,

int tree_width, int tree_height,

int x, int y, int R)

{

//это условие не выполняется, когда дерево состоит из одного элемента

if (tree_width != tree_height)

{

//коэффициент пропорциональности по оси Ох

int k_x = (window_width - 2 * (shift + R)) / (tree_width - 1);

//коэффициент пропорциональности по оси Оy

int k_y = (window_height - 2 * (shift + R)) / (tree_height - 1);

//x-координата узла

node_x = k_x * x + shift + R;

//у-координата узла

node_y = window_height - k_y * y - shift - R;

}

else

{

//x-координата узла

node_x = window_width / 2;

//у-координата узла

node_y = window_height / 2;

}

}
Ниже представлены реализация функции установления координат для текста и функции получения узла по координатам и радиусу.

Во вспомогательной функции get_help() применяется прямой обход по дереву, проверяя справедливость формулы окружности:

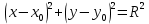(Формула 11)

, где x и y – координаты мыши, x0 и y0 – координаты центра окружности элемента, R – радиус данной окружности.

Если ни один элемент дерева не будет подходить по данной формуле, функция вернет NULL.
template

void Tree::setCoordsForText(int k, int R)

{

//х-координата первого символа текста

text_x = node_x - 3 * R / 4;

//у-координата первого символа текста

text_y = node_y - 3 * R / (4 * k);

}
template

Tree* Tree::getNodeByCoords(int x, int y, int R)

{

Tree* node = this;

node = get_help(node, x, y, R);

return node;

}
template

Tree* get_help(Tree* node, int x, int y, int R)

{

if (pow(x - node->node_x, 2) + pow(y - node->node_y, 2) <= pow(R, 2))

return node;

Tree* temp = NULL;

if (node->getLeft() != NULL)

temp = get_help(node->getLeft(), x, y, R);

if (temp != NULL)

return temp;

if (node->getRight() != NULL)

temp = get_help(node->getRight(), x, y, R);

return temp;

}
Чтобы формула нахождения координат элементов была справедлива, дерево должно быть полным. Для этого не случайно была объявлена переменная структуры tree, которая отныне будет хранить практически копию дерева, которое необходимо отобразить, только пополненного значениями NULL, не превышая высоту дерева. Сделаем мы это с помощью функции replaceNULLForEmpty(), ранее использованной в функции вертикальной печати.

Помимо изменений в переменной дерева, нужно инициализировать и другие глобальные переменные, обозначенные в структуре.

Первые два аргумента функции drawTree() берутся из аргументов main() и необходимы в дальнейшей инициализации, в связи с тем, что в данном примере приложение консольное, соответственно, может работать с консолью. Первый аргумент – это какое-либо число, а второй – массив символов.
template

void Tree::drawTree(

int argc, char** argv,

int window_width, int window_height,

int shift, int k)

{

Tree* temp = this->copyTree();

temp = temp->replaceNULLforEmpty();

glutContext.tree = temp;

glutContext.window_width = window_width;

glutContext.window_height = window_height;

glutContext.shift = shift;

glutContext.k = k;

initWindow(argc, argv);

}
Далее, опишем работу функции initWindow().

glutInit() инициализирует GLUT. Мы обязательно должны ее вызвать до того, как начнем использовать любые другие функции данной библиотеки

glutInitDisplayMode() задает режим дисплея, параметры GLUT_DOUBLE|GLUT_RGBA обозначают двойную буферизацию и четырехкомпонентный цвет.

glutInitWindowSize() по заданным ширине и высоте определяет окно.

glutCreateWindow() создает его с заголовком в качестве аргумента.

glutDisplayFunc() подключает дисплей.

glutReshapeFunc() подключает функцию обработки изменений размеров окна.

glutPassiveMotionFunc() подключает работу с мышью, в данном случае – пассивное движение мыши, обозначающее, что мы просто двигаем мышью, не совершая никаких нажатий на ее клавиши.

glutMainLoop() запускает главный цикл.
template

void initWindow(int argc, char** argv)

{

glutInit(&argc, argv);

glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGBA);

glutInitWindowSize(glutContext.window_width, glutContext.window_height);

glutCreateWindow("DrawTree");

glutDisplayFunc(display);

glutReshapeFunc(reshape);

glutPassiveMotionFunc(mouseMove);

glutMainLoop();

}

Функции изменений размеров окна, изображения линий и окружности

Реализуем функцию обработки изменений размеров окна.

glViewport() отвечает за вывод изображения, начиная с первых двух координат и заканчивая последними двумя.

glMaxtrixMode(GL_PROJECTION) и glMatrixMode (GL_MODELVIEW) подключают матрицу проекции и модельно-видовую матрицу, а glLoadIdentity() загружает единичную матрицу.

gluOrtho2D() по четырем аргументам определяет систему координат. Первый аргумент – абстрактное лево, второй – право, третий – низ, четвертый – верх. Так, слева-направо задается привычная нам ось Ох, а снизу-вверх – ось Оу. В данном случае Ох начинается нулем, а заканчивается численным значением ширины окна. А ось Оу начинается нулем и заканчивается численным значением высоты окна.

glutContext.window_width и glutContext.window_height инициализируют переменные размеров окна, а glutPostRedisplay() будет перерисовывать изображение в окне, если его два параметра будут меняться.
static void reshape(int w, int h)

{

glViewport(0, 0, (GLsize i)w, (GLsize i)h);

glMatrixMode(GL_PROJECTION);

glLoadIdentity();

gluOrtho2D(0, (GLsize i)w, 0, (GLsize i)h);

glMatrixMode(GL_MODELVIEW);

glLoadIdentity();

glutContext.window_width = w;

glutContext.window_height = h;

glutPostRedisplay();

}
Создадим и реализуем простейшую функцию рисования линии по координатам первой и второй точек.

glBegin(GL_LINES) говорит о том, что все отдельные пары вершин, написанные после него, будут соединяться линиями.

glColor3f(0.0, 0.0, 0.0) задает черный цвет.

glVertex2i(x1, y1) и glVertex2i(x2, y2) определяют, соответственно, конечные первую и вторую точку линии.

glEnd() говорит об окончании действия glBegin().
static void drawLine(int x1, int y1, int x2, int y2)

{

glBegin(GL_LINES);

glColor3f(0.0, 0.0, 0.0);

glVertex2i(x1, y1);

glVertex2i(x2, y2);

glEnd();

}
Реализуем функции изображения кругов и окружностей.

Обе функции используют три аргумента: x- и y-координаты в сочетании с радиусом R.

drawFillCircle() рисует сначала белый круг, а затем окаймляет его черным «ободком» - окружностью. Белый круг – это просто точки, x- и y-координаты которых задаются формулами:

x1=i*sin(t)+x	(Формула 12)
y1=i*cos(t)+y	(Формула 13)

где i – это часть или весь радиус, а t – градусная мера угла.

drawBlueCircle() рисует только окружность синего цвета.
static void drawFillCircle(int x, int y, int R)

{

glColor3f(1.0, 1.0, 1.0);

float x1, y1;

glBegin(GL_POINTS);

for (int i = 0; i <= R; i++) {

for (int t = 0; t <= 360; t++) {

x1 = i * sin(t) + x;

y1 = i * cos(t) + y;

glVertex2f(x1, y1);

}

}

glEnd();

glColor3f(0.0, 0.0, 0.0);

glBegin(GL_POINTS);

for (int i = R - 1; i <= R; i++) {

for (int t = 0; t <= 360; t++) {

x1 = R * sin(t) + x;

y1 = R * cos(t) + y;

glVertex2f(x1, y1);

}

}

glEnd();

}
static void drawBlueCircle(int x, int y, int R)

{

glColor3f(0.0, 0.0, 1.0);

float x1, y1;

glBegin(GL_POINTS);

for (int i = R - 1; i <= R; i++) {

for (int t = 0; t <= 360; t++) {

x1 = R * sin(t) + x;

y1 = R * cos(t) + y;

glVertex2f(x1, y1);

}

}

glEnd();

}

Реализуем функцию изображения текста

Функция использует в качестве аргументов текст неопределенного типа, который затем переводится в строковый; шрифт, координаты текста, радиус и коэффициент ширины данных.

glPushMatrix() - положить в стек текущую матрицу, а glPopMatrix() - вытащить со стека положенную туда матрицу.

Между этими двумя командами мы будем делать различные расчеты и рисовать текст.

glTranslatef() – это переход в точку, с которой нужно начать что-либо рисовать.

После нее следует преобразование строки из типа string, сконвертированного из типа Т, в тип char*.

Затем идет прохождение по массиву char* и с помощью функции glutStrokeWidth() получается целочисленное значение ширины каждого символа. Из всех значений выбирается максимальное.

По формулам:

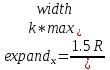,	(Формула 14)
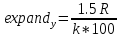	(Формула 15)

определяется коэффициент расширения для осей Ох и Оу, чтобы масштабировать текст.

Условимся, что максимальная высота символа = 100 пикселей, но это только для цифр. Можно, конечно, посчитать и для других символов, но нет необходимости вычислять пиксели и для них, пусть пока что для ознакомления будет достаточно цифр.

glScalef() масштабирует символы текста, а glStrokeCharacter() выводит.
template

static void drawText(T text, void* font, int text_x, int text_y, int R, int k)

{

glColor3f(0.0, 0.0, 0.0);

glPushMatrix();

glTranslatef(text_x, text_y, 0.0);

string s = to_string(text);

char* s1 = newchar[s.size() + 1];

for (int i = 0; i < s.size(); i++) {

s1[i] = s.at(i);

}

s1[s.size()] = 0;

char* c;

int max_char_width = 0;

int char_width = 0;

for (c = s1; *c != '\0'; c++) {

char_width = glutStrokeWidth(font, *c);

if (max_char_width < char_width) max_char_width = char_width;

}

float expand_x = (float)1.5 * R / (float)(k * max_char_width);

float expand_y = (float)1.5 * R / (float)(k * 100);

glScalef(expand_x, expand_y, 1.0);

for (c = s1; *c != '\0'; c++)

glutStrokeCharacter(font, *c);

glPopMatrix();

}
Простейший пример использования glutBitmapCharacter():
void draw_string_bitmap(void* font, const char* string)

{

while (*string)

glutBitmapCharacter(font, *string++);

}
// далее где-то в коде

glRasterPos2f(0, 0);

draw_string_bitmap(GLUT_BITMAP_HELVETICA_18, "Hello!");
Для рисования текста с помощью Bitmap достаточно указать позицию с помощью glRasterPos2f() и посимвольно вывести каким-либо шрифтом, например GLUT_BITMAP_HELVECITCA_18, какую-либо строчку. Однако, этот шрифт нельзя масштабировать самостоятельно, из-за чего приходится пользоваться уже готовыми вариантами размеров данного шрифта.

Легче уследить по математической зависимости за поведением векторного шрифта, чем за поведением растрового, учитывая его ограничения в масштабировании. Вследствие этого оперируем именно glutStrokeCharacter().

Организация функции display()

Первая часть функции – это инициализация и расчеты.

Во временные переменные копируются значения соответствующих глобальных переменных. Определяется высота дерева и минимальная ширина дерева – как в функции вертикальной печати. Инициализируются первоначальные значения известных переменных текущего уровня, индекса и числа пробелов для корня.

Задаются структура и два списка.

Далее, идет расчет радиуса для каждого из элементов дерева по ширине, высоте окна и ширине дерева. Именно здесь устанавливается глобальная переменная R.

Просчитываются координаты для первого узла – корня, обновляются списки и структура элемента.
void display(void) {

Tree* tree = (Tree*)glutContext.tree;

int k = glutContext.k;

int window_width = glutContext.window_width;

int window_height = glutContext.window_height;

int shift = glutContext.shift;

int height = tree->getHeight();

int maxLeafs = pow(2, height - 1); //максимальное число листов на нижнем уровне (нумерация с нуля)

int width = 2 * maxLeafs - 1; //минимальная ширина дерева для печати (не конечная, но необходимая)

int curLevel = 0; //номер строки (на выводе)

int index = 0; //номер элемента в строке (нумерация с нуля)

intfactSpaces = getPos(index, width, curLevel, height - 1); //позиция корня (число пробелов перед ним)

pos node;

vector*> V;

vector
Vi;

int R; //радиускруга

R = (window_width - 2 * shift) / (2 * width);

if (2 * R * height > (window_height - 2 * shift)) R = (window_height - 2 * shift) / (2 * height);

glutContext.R = R;

tree->setCoordsForNode(window_width, window_height, shift, width, height, factSpaces, curLevel, R); //установили координаты корня при рисовании

V.push_back(tree);

node.col = factSpaces;

node.str = curLevel;

Vi.push_back(node);

. . .

glClearColor() устанавливает белый цвет экрана, glClear() очищает его, glLineWidth() устанавливает ширину линии, с помощью которой будут отображаться в дальнейшем соединительные линии между вершинами, glEnable() с данным параметром устанавливает режим сглаживания.

Далее, реализуется обычное поперечное прохождение по дереву, какое использовалось в функции вертикальной печати.

При условии, что потомок слева имеет данные, не равные NULL, будет отображаться линия в его сторону, начиная с текущего элемента. То есть если у узла А слева узел с данными NULL, линия между ними чертиться не будет.

. . .

glClearColor(1.0, 1.0, 1.0, 1.0);

glClear(GL_COLOR_BUFFER_BIT);

glLineWidth(2);

glEnable(GL_POINT_SMOOTH);

for (int i = 0; i < tree->getAmountOfNodes(); i++) {

if (pow(2, curLevel) <= index + 1) {

index = 0;

curLevel++;

}

if (V.at(i)->getLeft() != NULL) {

V.push_back(V.at(i)->getLeft());

factSpaces = getPos(index, width, curLevel, height - 1);

node.col = factSpaces;

node.str = curLevel;

Vi.push_back(node);

index++;

V.at(i)->getLeft()->setCoordsForNode(window_width, window_height, shift, width, height, factSpaces, curLevel, R);

if (V.at(i)->getLeft()->getData() != NULL) {

int x1 = V.at(i)->node_x;

int y1 = V.at(i)->node_y;

int x2 = V.at(i)->getLeft()->node_x;

int y2 = V.at(i)->getLeft()->node_y;

drawLine(x1, y1, x2, y2);

}

}

}

. . .

Аналогичным образом идет работа с правыми потомками:

. . .

if (V.at(i)->getRight() != NULL) {

V.push_back(V.at(i)->getRight());

factSpaces = getPos(index, width, curLevel, height - 1);

node.col = factSpaces;

node.str = curLevel;

Vi.push_back(node);

index++;

V.at(i)->getRight()->setCoordsForNode(window_width, window_height, shift, width, height, factSpaces, curLevel, R);

if (V.at(i)->getRight()->getData() != NULL) {

int x1 = V.at(i)->node_x;

int y1 = V.at(i)->node_y;

int x2 = V.at(i)->getRight()->node_x;

int y2 = V.at(i)->getRight()->node_y;

drawLine(x1, y1, x2, y2);

}

}

. . .

Только после того, как нарисовались линии, нужно отобразить круги, а затем и текст.

Делается это все при условии, что данные таких элементов не равны NULL.

Затем проверяется значение переменной state. Если она равна 0, нарисуется просто белый круг, окаймленный черной окружностью.

В противном случае, допустим 1, нарисуется белый круг, окаймленный синей окружностью. То есть при наведении мыши (функцию работы с мышью мы рассмотрим позже). Но произойдет это, если координаты данного узла будут соответствовать области, в которой сейчас находится курсор.

Далее, рисуется текст и заканчивается цикл.

Напоследок после рисования нужно попросить OpenGL сменить экранные буфера при помощи glutSwapBuffers(), ведь у нас включена двойная буферизация.

glDisable() отключает сглаживание при таком параметре.

. . .

if (V.at(i)->getData() != NULL) {

if (glutContext.state == 0) {

drawFillCircle(V.at(i)->node_x, V.at(i)->node_y, R);

}

else {

drawFillCircle(V.at(i)->node_x, V.at(i)->node_y, R);

if ((tree->getNodeByCoords(glutContext.x, glutContext.y, R)->node_x == V.at(i)->node_x)

& (tree->getNodeByCoords(glutContext.x, glutContext.y, R)->node_y == V.at(i)->node_y))

drawBlueCircle(V.at(i)->node_x, V.at(i)->node_y, R);

}

V.at(i)->setCoordsForText(k, R);

drawText(V.at(i)->getData(), GLUT_STROKE_ROMAN, V.at(i)->text_x, V.at(i)->text_y, R, k);

}

}

glutSwapBuffers();

glDisable(GL_POINT_SMOOTH);

}

Дополнительно

Деление экрана пополам так же справедливо для рисования дерева отдельно для каждого уровня. Например, корень дерева должен располагаться по центру, соответственно, его x-координата – численно половина ширины окна (учтем то, что нужно вычесть два отступа). Его потомок слева имеет x-координату, расположенную по середине между левой границей рисования дерева и x-координатой своего родителя – корня. Потомок справа находится ровно в середине между x-координатой корня и правой границей. Все узлы на последующих уровнях так же будут располагаться в середине пространства, ограниченного слева и справа x-координатами ближайших по оси Ох узлов.

Для этого в функцию setCoordsForNode() вместо аргумента factSpaces, представляющего собой количество пробелов перед узлом (если бы это был вывод дерева в консоли), нужно поместить аргумент index, идентифицирующий индекс элемента отдельного уровня-массива.

И теперь node_x – x-координата узла будет высчитываться по такой формуле:

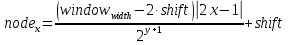(Формула 16)

Соответственно, в самой функции node_x будет высчитываться иначе:

node_x = (window_width-2*shift)*abs(2*x-1)/pow(2,y+1)+shift;

(Формула 17)

В отличие от предыдущего варианта вычисления node_x этот справедлив как для корня, так и для любого другого узла.

Работа с мышью в OpenGL

Регистрация нажатий мыши

GLUT предлагает Вам способ, чтобы зарегистрировать функцию, которая будет отвечать за обработку событий, создаваемых нажатиями клавиш мыши. Название этой функции glutMouseFunc(). Синтаксис выглядит следующим образом:

void glutMouseFunc(void (*func)(int button, int state, int x, int y));

Параметры:

*func - имя функции, которая будет обрабатывать события мыши.

Как видно, с момента подписания glutMouseFunc(), функция, которая будет обрабатывать события мыши, должна иметь 4 параметра. Первый из них касается того, какая кнопка была нажата или отпущена. Этот аргумент может иметь одно из трех значений:

25. 
    GLUT_LEFT_BUTTON;
    
26. 
    GLUT_MIDDLE_BUTTON;
    
27. 
    GLUT_RIGHT_BUTTON;
    

Второй аргумент относится к состоянию кнопки, то есть идентификации момента нажатия и отпускания кнопки. Возможные значения:

25. 
    GLUT_DOWN;
    
26. 
    GLUT_UP;
    

Если ответный вызов генерируется со статусом GLUT_DOWN, приложение может предположить, что GLUT_UP будет после этого события, даже если мышь перемещается за пределы окна. Остальные два параметра обеспечивают (х, у) координаты мыши относительно левого верхнего угла рабочей области окна.

Определение перемещения мыши

GLUT дает возможность обнаружения движения мыши для нашего приложения. Есть два типа движения для GLUT: активные и пассивные движения. Активное движение происходит при перемещении мыши и нажатия кнопки. Пассивные движения, когда мышь движется, но ни одна кнопка не нажата. Если приложение отслеживает движение манипулятора, будет сгенерировано событие в кадре во время периода, когда мышь движется.

Нужно зарегистрировать функцию, которая будет отвечать за обработку событий движения. Определено две различных функции: одна для отслеживания пассивных движений, а другая, чтобы отслеживать активные движения.

Синтаксис GLUT функций слежения за перемещением:

void glutMotionFunc(void (*func) (int x,int y));

void glutPassiveMotionFunc(void (*func) (int x, int y));

Параметры:

*func - функция, которая будет отвечать за соответствующий тип движения.

Параметры функции обработки движения мыши являются (х, у) декартовы координаты курсора мыши относительно левого верхнего угла рабочей области окна.

Обнаружение попадания или выхода из рабочей области окна курсора мыши

GLUT может определять, когда мышь покидает или входит в рабочую область окна. Зарегистрируем функцию обратного вызова для обработки этих двух событий. GLUT функцией регистрации является обратный вызов glutEntryFunc() и синтаксис выглядит следующим образом:

void glutEntryFunc(void (*func)(int state));

Параметры:

*func - функция, которая будет обрабатывать эти события.

Параметр функции, которая будет обрабатывать эти события, сообщает нам, если мышь попадает в левую область окна. GLUT определяет две константы, которые можно использовать в приложении[22]:

25. 
    GLUT_LEFT;
    
26. 
    GLUT_ENTERED;
    

Реализуем функцию работы с мышью.

Функция работы с мышью в качестве аргументов принимает текущие координаты курсора. Затем по функции нахождения узла по этим координатам определяется, попадает ли курсор в нужную область.

О том, что он не попадает, сообщит функция getNodeByCoords(), вернув значение NULL. Тогда придадим глобальной переменной state значение 0. Учтем: в функции display() это значение говорило о том, что соответствующий узел будет нарисован по умолчанию, то есть белый круг и черная окружность вокруг него.

Если значение не равно NULL, обновятся глобальные переменные x и y полученными значениями, обновится переменная state, допустим, значением 1.

В обоих случаях необходимо перерисовать изображение с помощью функции glutPostRedisplay().
template

static void mouseMove(int x, int y) {

Tree* tree = (Tree*)glutContext.tree;

int R = glutContext.R;

Tree* node = tree->getNodeByCoords(x, glutContext.window_height - y, R);

if (node != NULL) {

glutContext.x = x;

glutContext.y = glutContext.window_height - y;

glutContext.state = 1;

glutPostRedisplay();

}

else {

glutContext.state = 0;

glutPostRedisplay();

}

}
В итоге составим дерево на рисунке 4 по программному коду:
vector arr = { 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24 };

Tree* tree = newTree(arr.at(0));

for (int i = 0; i < arr.size(); i++) {

int left = 2 * i + 1;

int right = left + 1;

if (left < arr.size()) {

tree->findElement_insertLeft(tree, arr.at(i), arr.at(left));

}

if (right < arr.size()) {

tree->findElement_insertRight(tree, arr.at(i), arr.at(right));

}

}

tree->drawTree(argc, argv, 800, 600, 10, 2);


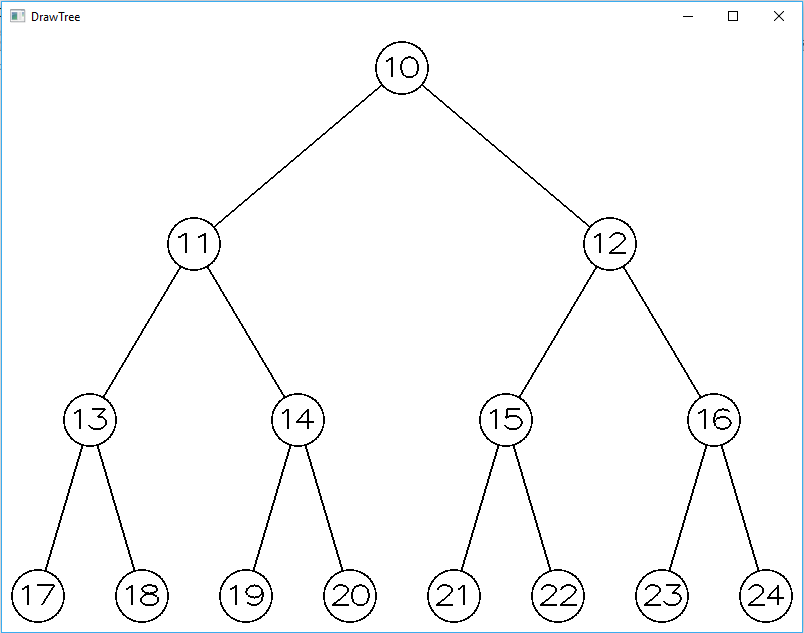
Рисунок 4 – изображение полного дерева

---

Смотрите также файлы

• Тема 15. Правовые и организационные основы деятельности коммерческих банков в Российской федерации.docx

• Составление рациональных режимов дня для различных возрастных групп.docx

• 6В01302 Бастауышта оыту педагогикасы мен дістемесі білім беру бадарламасыны 1 курс студенттеріне арналан Ерекше білім беруге мтаж балалармен бастауыш мектеп маліміні жмыс мазмны.docx

• Программа рылымы шін мселені алыптасттыруды маыздылыын тжырымдайды.docx

• Коррупция понятие, виды, причины.docx