ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 45
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Введение в теорию графов
Графом называется множество узлов и связей между ними. Каждый узел называется вершиной, а каждая связь – ребром. Каждое ребро соединяет две вершины.Виды графов
Графы делятся на ориентированные и неориентированные. Ориентированный граф – такой граф, в котором можно двигаться от вершины к вершине только в одном направлении. Например, на рисунке 1 можно двигаться из вершины v0 в v1, а из v1 в v0 нельзя. В неориентированных графах можно двигаться в обе стороны. Например, на рисунке 2 из вершины 1 можно двигаться в вершину 2, и наоборот.
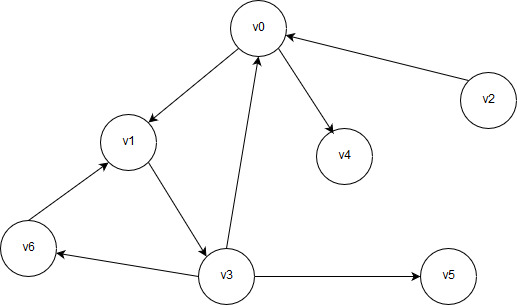
Рисунок 1 – Ориентированный граф
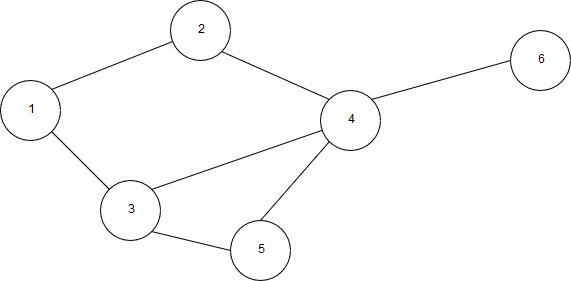
Рисунок 2 – Неориентированный граф
Граф, в котором присутствуют как ориентированные ребра, так и неориентированные, называется смешанным.
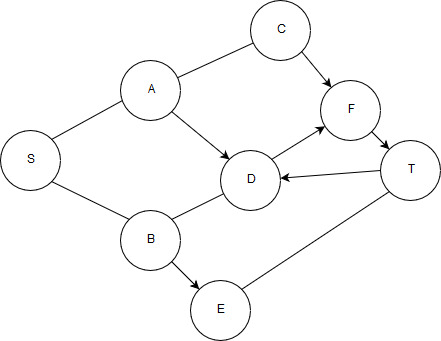
Рисунок 3 – Смешанный граф
Кроме того, графы делятся на взвешенныеи невзвешенные. Граф, в котором каждому ребру в соответствие поставлено некоторое числовое значение – вес, называется взвешенным графом (например, длина дороги). Если никакого числового значения рёбрам не поставлено, то граф называется невзвешенным. Чаще всего, в названии графа указывают как его ориентированность или неориентированность, так и его взвешенность или невзвешенность.
Граф, в котором между любой парой вершин существует, как минимум, один путь, называется связным. Если в графе существует хотя бы одна вершина, не связанная с другими, он называется несвязным.
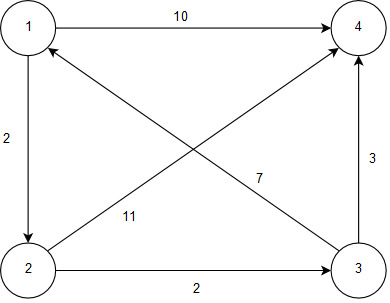
Рисунок 4 – Взвешенный связанный ориентированный граф
Граф, в котором число рёбер близко к максимальному (когда каждая вершина графа связана с любой другой вершиной графа рёбрами), называется
плотным графом.
Граф с противоположным свойством, имеющий малое число рёбер, называется разреженным графом.
Петлёй называется ребро, которое соединяет вершины v1 и v2, причём v1 и v2 совпадают. Иными словами, петля – это ребро, которое начинается и заканчивается в одной вершине.
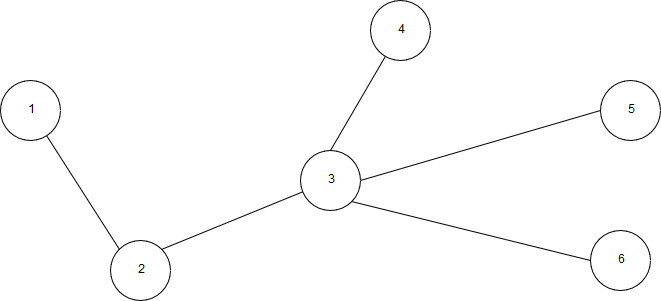
Рисунок 5 – Несвязный граф
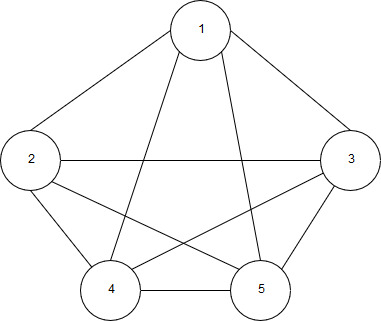
Рисунок 6 – Плотный граф
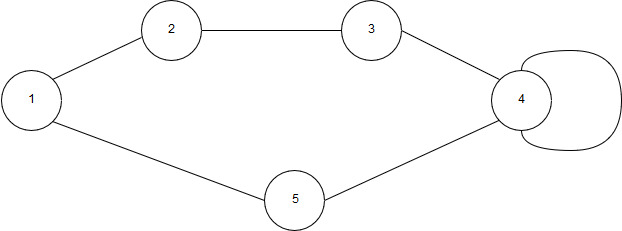
Рисунок 7 – Граф с петлёй
Инцидентность – понятие, используемое только в отношении ребра и вершины. Если v1, v2 - вершины, а e = (v1, v2) - соединяющее их ребро, тогда вершина v1 и ребро e инцидентны, вершина v2 и ребро e тоже инцидентны. Две вершины (или два ребра) инцидентными быть не могут. Например, на рисунке 7 вершина 1 инцидентна ребру 1-2.
Смежность – понятие, используемое в отношении только двух рёбер, либо только двух вершин: два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными. Например, на рисунке 7 вершины 1 и 2 смежные, поскольку инциденты одному ребру.
Маршрутомназывается такая чередующаяся последовательность вершин и рёбер vertex0, edge1, vertex1, edge2, vertex2,….edgek, vertexk, v 0 , e 1 , v 1 , e 2 , v 2 , . . . , e k , v k {\displaystyle v_{0},e_{1},v_{1},e_{2},v_{2},...,e_{k},v_{k}} …..//в которой любые два соседних элемента инцидентны. Если v 0 = v k {\displaystyle v_{0}=v_{k}} vertex0 = vertexk, то маршрут замкнут, иначе маршрут открыт.
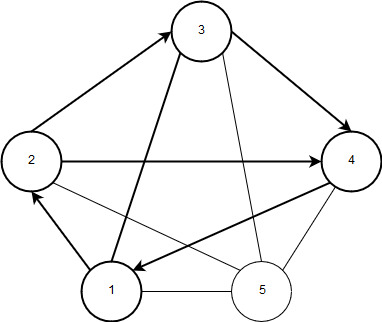
Рисунок 8 – Открытый маршрут (вершины 2-4-1-2-3-4-1).
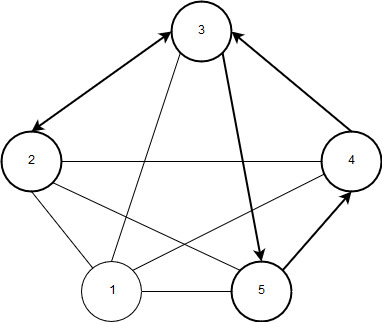
Рисунок 9 – Замкнутый маршрут (вершины 2-3-5-4-3-2)
Цепь – маршрут, все ребра которого различны. Если все вершины такого маршрута различны, то цепь называется
простой. В цепи vertex0, edge1, ….., edgek, vertexk вершины vertex0 и vertexk называются концами цепи.
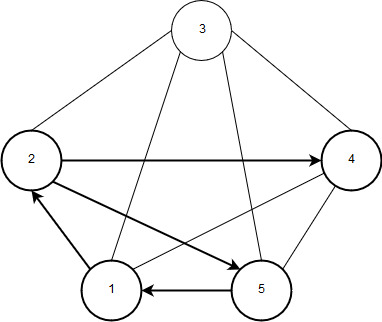
Рисунок 10 – Открытая цепь (вершины 2-5-1-2-4)
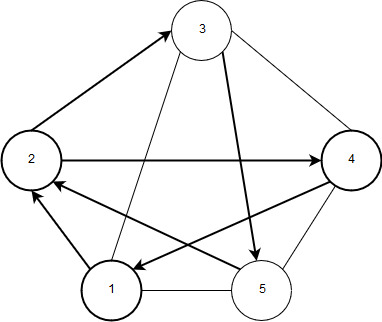
Рисунок 11 – Замкнутая цепь (вершины 2-4-1-2-3-5-2)
Циклом называется замкнутая цепь (см. рисунок 11).
Представление графов. Матрица смежности
Матрица смежности графа – это квадратная матрица, в которой каждый элемент принимает одно из двух значений: 0 или 1 для невзвешенного графа. Значения 1 и 0 отображают существование ребра между вершинами: если между вершинами 1 и 2 есть ребро, то в матрице на пересечении первой строки и второго столбца и второй строки и первого столбца будут стоять единицы. Если граф взвешенный, то элементами матрицы смежности будут числа, соответствующие весам ребер, соединяющих вершины, на пересечении которых в таблице стоит элемент.
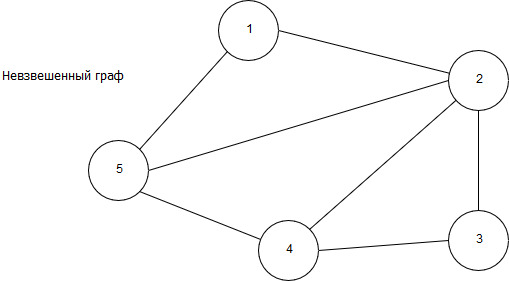
Рисунок 12 – Невзвешенный неориентированный граф
Матрица смежности для графа, изображенного на рисунке 7, представлена следующим образом:
| № вершины | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 2 | 1 | 0 | 1 | 1 | 1 |
| 3 | 0 | 1 | 0 | 1 | 0 |
| 4 | 0 | 1 | 1 | 0 | 1 |
| 5 | 1 | 1 | 0 | 1 | 0 |
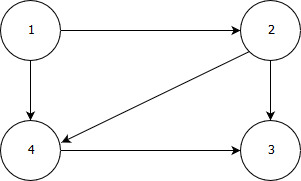
Рисунок 13 – Невзвешенный ориентированный граф
Матрица смежности для графа, изображенного на рисунке 8, представлена следующим образом:
| № вершины | 1 | 2 | 3 | 4 |
| 1 | 0 | 1 | 0 | 1 |
| 2 | 0 | 0 | 1 | 1 |
| 3 | 0 | 1 | 0 | 0 |
| 4 | 1 | 0 | 1 | 0 |
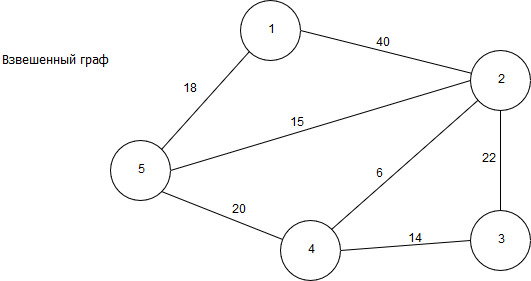
Рисунок 14 – Взвешенный неориентированный граф
Матрица смежности для графа, изображенного на рисунке 9, представлена следующим образом:
| № вершины | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 40 | 0 | 0 | 18 |
| 2 | 40 | 0 | 22 | 6 | 15 |
| 3 | 0 | 22 | 0 | 14 | 0 |
| 4 | 0 | 6 | 14 | 0 | 22 |
| 5 | 18 | 15 | 0 | 20 | 0 |
Граф может быть представлен с помощью вектора смежности. В векторе смежности для каждой вершины хранятся номера смежных с ней вершин.
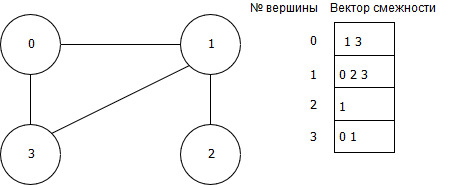
Рисунок 15 – Представление графа с помощью вектора смежности
Еще одной формой представления графа является матрица инцидентности, в которой указываются связи между инцидентными элементами графа (ребра и вершины). Столбцы матрицы соответствуют ребрам, строки – вершинам. Ненулевое значение в ячейке матрицы указывает на связь между вершиной и ребром (их инцидентность).
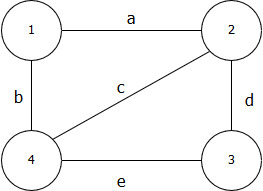
Рисунок 16 – Взвешенный неориентированный граф
Матрица инцидентности, соответствующая графу, выглядит следующим образом:
| № вершины | a | b | c | d | e |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 1 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 1 | 0 | 1 |