ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 47
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Приведем пример построения матрицы инцидентности для взвешенного ориентированного графа
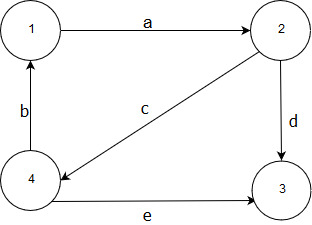
Рисунок 17 – Пример матрицы инцидентности для ориентированного графа
Матрица инцидентности, соответствующая графу, выглядит следующим образом:
| № вершины | a | b | c | d | e |
| 1 | 1 | -1 | 0 | 0 | 0 |
| 2 | -1 | 0 | 1 | 1 | 0 |
| 3 | 0 | 0 | 0 | -1 | -1 |
| 4 | 0 | 1 | -1 | 0 | 1 |
Список смежности – один из способов представления графа в виде коллекции списков вершин. Каждой вершине графа соответствует список, состоящий из "соседей" этой вершины. Если граф взвешенный, то рядом с номером вершины-соседа также указывается длина ребра до этого соседа.
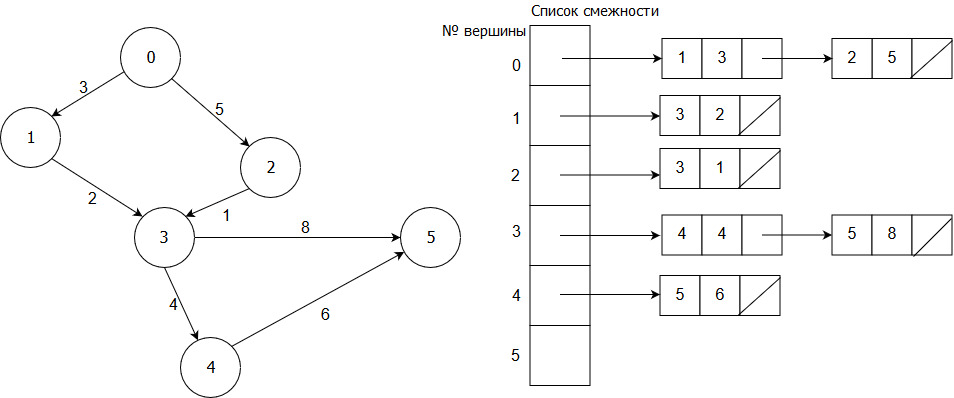
Рисунок 18 – Cписок смежности для ориентированного взвешенного графа
Если хватает памяти компьютера, то матрицу смежности реализовать и применить легче, чем списки смежности. В графе, представленном списком смежности, удобно искать вершины, смежные с данной, добавлять ребра и вершины, работать с разреженными графами. Однако, при таком представлении неудобно удалять элемент и выполнять поиск элемента.
Проектирование графов на алгоритмическом языке С++
В программном представлении графа работают с матрицей смежности, так как при ее использовании удобнее выполнять поиск элемента.
Создается класс Graph, он будет шаблонным, чтобы узел графа мог содержать данные разного типа (например, строки или числа). Перед описанием класса объявляется целочисленная константа – максимальный размер матрицы смежности (пусть она равна 20).
Граф будет представлен следующим образом: все вершины графа заносятся в вектор вершин (вектор – это контейнер из библиотеки STL (Standard Template Library [18]), где индекс каждой вершины соответствует ее индексу в матрице смежности. Например, если в векторе вершин у вершины индекс [1], то в матрице смежности эта вершина располагается по индексу [1][1]. В приватном (private) поле класса Graph хранится вектор вершин vertList (от vertex list) и матрица смежности (размером 20х20). Для работы с графом в поле public описаны следующие методы:
Конструктор Graph()
В нем происходит заполнение матрицы смежности нулями.
Названия переменных составлены таким образом, что они отображают смысл того, для чего они предназначены. Здесь: Graph – это имя класса, maxSize – максимальный размер матрицы смежности, adjMatrix (от adjacency matrix) – матрица смежности.
Код конструктора:
template //объявление шаблона с формальным параметром класс Т
Graph::Graph() { //конструктор, который инициализирует значения объектов класса Graph
//перебор строк и столбцов матрицы смежности и заполнение её нулями
for (int i = 0; i < maxSize; ++i) {
for (int j = 0; j < maxSize; ++j) {
this->adjMatrix[i][j] = 0;
}
}
}
Деструктор
Graph()
template
Graph::
Graph() {Проектирование графов на алгоритмическом языке С++
В программном представлении графа работают с матрицей смежности, так как при ее использовании удобнее выполнять поиск элемента.
Создается класс Graph, он будет шаблонным, чтобы узел графа мог содержать данные разного типа (например, строки или числа). Перед описанием класса объявляется целочисленная константа – максимальный размер матрицы смежности (пусть она равна 20).
Граф будет представлен следующим образом: все вершины графа заносятся в вектор вершин (вектор – это контейнер из библиотеки STL (Standard Template Library [18]), где индекс каждой вершины соответствует ее индексу в матрице смежности. Например, если в векторе вершин у вершины индекс [1], то в матрице смежности эта вершина располагается по индексу [1][1]. В приватном (private) поле класса Graph хранится вектор вершин vertList (от vertex list) и матрица смежности (размером 20х20). Для работы с графом в поле public описаны следующие методы:
Конструктор Graph()
В нем происходит заполнение матрицы смежности нулями.
Названия переменных составлены таким образом, что они отображают смысл того, для чего они предназначены. Здесь: Graph – это имя класса, maxSize – максимальный размер матрицы смежности, adjMatrix (от adjacency matrix) – матрица смежности.
Код конструктора:
template
Graph
//перебор строк и столбцов матрицы смежности и заполнение её нулями
for (int i = 0; i < maxSize; ++i) {
for (int j = 0; j < maxSize; ++j) {
this->adjMatrix[i][j] = 0;
}
}
}
Деструктор
Graph
}
Метод int GetVertPos(const T& vertex).
Находит позицию вершины в векторе вершин. Сравнивает вершину, ссылку на которую получил, с каждой вершиной в векторе. Как только будет найдено совпадение - возвращается номер этой вершины. Если ни одного совпадения не было, возвращается число, которое равно (-1).
GetVertPos(const T& vertex) - GetVertexPosition - получить позицию вершины типа Т; vertList -это список вершин; IsEmpty – является ли пустым; IsFull – является ли полным. GetAmountVerts - получить количество вершин; GetAmountEdges – получить количество ребер; amount - количество; vertListSize - размер списка вершин.
Код метода int GetVertPos(const T& vertex):
template
int Graph
for (int i = 0; i < this->vertList.size(); ++i) {
if (this->vertList[i] == vertex)
return i;
}
return -1;
}
Метод bool IsEmpty()
Проверяет, пуст ли граф, то есть в нём нет ни одной вершины. Проверяется, пуст ли вектор вершин. Если да, то возвращает значение true, если нет, то false.
Код метода bool IsEmpty():
template
bool Graph
if (this->vertList.size() != 0)
return false;
else
return true;
}
Метод bool IsFull()
Проверяет, достигло ли количество вершин в графе максимально возможного предела (для нашего примера это 20). Если размер вектора вершин равен 20, то метод вернет true, если меньше, то false. Если граф пуст, то метод вернет false.
Код метода bool IsFull():
template
bool Graph
return (vertList.size() == maxSize);
}
Метод int GetAmountVerts().
Метод возвращает количество вершин в графе, то есть размер вектора вершин. Если граф пуст, то метод вернет 0.
Код метода int GetAmountVerts().
template
int Graph
return this->vertList.size();
}
Метод int GetAmountEdges()
Метод возвращает количество ребер в графе. Для каждой из вершин графа в цикле проверяется: если в матрице смежности данные ячейки с индексами [i][j] равны данным ячейки с индексами [j][i] и это значение не ноль, то найден вес ребра, соединяющего две вершины. В конце, после цикла, он делится нацело на 2 (если граф неориентированный). Деление на 2 нужно потому, что в неориентированном графе и в ячейке [i][j], и в ячейке [j][i] значение одно и то же. Это означает, что в цикле одно и то же значение будет посчитано 2 раза: сначала для ячейки [i][j], затем для ячейки [j][i]. Следовательно, между каждыми двумя вершинами к концу работы цикла будет по 2 ребра, что неправильно, поскольку рёбер изначально было по одному между каждыми двумя вершинами. Поэтому нужно итоговое значение счетчика поделить нацело на 2, чтобы результат был корректным. Если граф ориентированный, то деление на 2 и проверка на равенство элемента [i][j] элементу [j][i] не нужны. Если граф невзвешенный (до этого был описан алгоритм для взвешенных графов), то в условии проверяется равенство элемента матрицы смежности единице, если граф ориентированный, то только элемента [i][j], если граф неориентированный, то элементов [i][j] и [j][i].
Код метода GetAmountEdges() для взвешенного ориентированного графа:
template
int Graph
int amount = 0; // обнуляем счетчик
if (!this->IsEmpty()) { // проверяем, что граф не пуст
for (int i = 0, vertListSize = this->vertList.size(); i < vertListSize; ++i) {
for (int j = 0; j < vertListSize; ++j) {
if (this->adjMatrix[i][j] == 1) // находим рёбра
amount += 1; // считаем количество рёбер
}
}
return amount; // возвращаем количество рёбер
}
else
return 0; // если граф пуст, возвращаем 0
}
Код метода GetAmountEdges() для взвешенного неориентированного графа:
template
int Graph
int amount = 0; // обнуляем счетчик
if (!this->IsEmpty()) { // проверяем, что граф не пуст
for (int i = 0, vertListSize = this->vertList.size();
i < vertListSize; ++i) {
for (int j = 0; j < vertListSize; ++j) {
if (this->adjMatrix[i][j] ==
this->adjMatrix[j][i] &&
this->adjMatrix[i][j] != 0) // находим рёбра
amount += 1; // считаем количество рёбер
}
}
return (amount / 2); // приводим счетчик к корректному результату и возвращаем его
}
else
return 0; // если граф пуст, возвращаем 0
}
Код метода GetAmountEdges() для невзвешенного ориентированного графа:
template
int Graph
int amount = 0; // обнуляем счетчик
if (!this->IsEmpty()) { // проверяем, что граф не пуст
for (int i = 0, vertListSize = this->vertList.size(); i < vertListSize; ++i) {
for (int j = 0; j < vertListSize; ++j) {
if (this->adjMatrix[i][j] == 1) // находим рёбра
amount += 1; // считаем количество рёбер
}
}
return amount; // возвращаем количество рёбер
}
else
return 0; // если граф пуст, возвращаем 0
}
Код метода GetAmountEdges() для невзвешенного неориентированного графа:
template
int Graph
int amount = 0; // обнуляем счетчик
if (!this->IsEmpty()) { // проверяем, что граф не пуст
for (int i = 0, vertListSize = this->vertList.size(); i < vertListSize; ++i) {
for (int j = 0; j < vertListSize; ++j) {
if (this->adjMatrix[i][j] == 1 && this->adjMatrix[j][i] == 1) // находим рёбра
amount += 1; // считаем количество рёбер
}
}
return (amount / 2); // приводим счетчик к корректному результату и возвращаем его
}
else
return 0; // если граф пуст, возвращаем 0
}
Метод int GetWeight(const T& vertex1, const T& vertex2)
Метод возвращает вес ребра, соединяющего вершины vertex1 и vertex2, ссылки на которые метод принимает. Сначала производится проверка, что граф не пуст, затем вычисляются позиции вершин vertex1 и vertex2 в графе и из матрицы смежности извлекается значение на пересечении этих вершин. В невзвешенных графах этот метод не используется.
GetWeight - получить вес, vertPos1 - позиция первой вершины, vertPos2 - позиция второй вершины, vertex1 - исходная вершина, vertex2 – конечная вершина (в которую идёт ребро, вес которого ищет функция).
Код метода GetWeight(const T & vertex1, const T & vertex2):
template
int Graph
if (!this->IsEmpty()) {
int vertPos1 = GetVertPos(vertex1);
int vertPos2 = GetVertPos(vertex2);
return adjMatrix[vertPos1][vertPos2];
}
return 0;
}
Метод std::vector
Рассмотрим граф, представленный на рисунке 19:
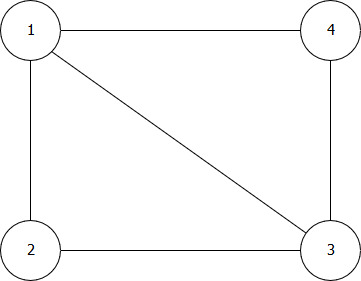
Рисунок 19 – Невзвешенный неориентированный граф
Матрица смежности, соответствующая графу, выглядит следующим образом:
| № вершины | 1 | 2 | 3 | 4 |
| 1 | 0 | 1 | 1 | 1 |
| 2 | 1 | 0 | 1 | 0 |
| 3 | 1 | 1 | 0 | 1 |
| 4 | 1 | 0 | 1 | 0 |
Опишем, как работает метод GetNbrs на примере приведенного выше графа. Но перед описанием непосредственно работы алгоритма рассмотрим матрицу смежности. После её анализа можно сделать следующие выводы:
-
Для вершины 1 соседями являются вершины 2,3,4; -
Для вершины 2 соседями являются вершины 1 и 3 -
Для вершины 3 соседями являются вершины 1,2,4 -
Для вершины 4 соседями являются вершины 1 и 3.
Сначала метод получает вершину, соседей которой необходимо найти. Пусть требуется найти соседей вершины 1. Алгоритм работает следующим образом:
Создаётся список, состоящий из соседей (изначально он пуст) – nbrsList. В матрице смежности вычисляется позиция вершины, соседей которой необходимо найти. Вершина 1 имеет позицию [1][1] – пересечение первой строки и первого столбца. В специальную переменную запоминается значение 1.
Затем в ходе циклического процесса проверяется, что элемент с индексом строки как у вершины 1 и индексом столбца i не равен 0 и что элемент с индексом строки i и индексом столбца, равным индексу строки у вершины 1, не равен 0. Если это так, то найден сосед, он заносится в список соседей. Например, проверяется элемент [1][2]: обнаруживается, что он не равен нулю. То есть между вершиной 1 и вершиной 2 есть ребро. Далее проверяется, что находится в ячейке [2][1]. Там тоже находится не ноль, значит, от вершины 2 до вершины 1 есть ребро, значит, они соседи. Вершина 2 заносится в список соседей. Подобные действия выполняются для других вершин. Если бы граф был ориентированный, то в циклическом процессе для поиска соседей проверялось бы, что в ячейках с индексом вершины 1 и индексом столбца i находятся не нули, а вторая проверка отсутствовала бы.
Функция возвращает список соседей.
Таким образом, в списке соседей окажутся вершины 2,3,4. После анализа матрицы смежности было выяснено, что соседями вершины 1 являются вершины 2,3,4. Значит, функция работает корректно.
Код метода GetNbrs(const T& vertex) для взвешенного и невзвешенного ориентированных графов:
template
std::vector
std::vector
int pos = this->GetVertPos(vertex); /* вычисление позиции vertex в матрице смежности */
if (pos != (-1)) { /* проверка, что vertex есть в матрице смежности */
for (int i = 0, vertListSize = this->vertList.size(); i < vertListSize; ++i) {
if (this->adjMatrix[pos][i] != 0) /* вычисление соседей*/
nbrsList.push_back(this->vertList[i]); /* запись соседей в вектор */
}
}
return nbrsList; // возврат списка соседей
}
Код метода GetNbrs(const T& vertex) для взвешенного и невзвешенного неориентированных графов:
template
std::vector
std::vector
int vertPos = this->GetVertPos(vertex); // вычисление позиции vertex в матрице смежности
if (vertPos != (-1)) { проверка, что vertex есть в матрице смежности
for (int i = 0, vertListSize = this->vertList.size(); i < vertListSize; ++i) {
if (this->adjMatrix[vertPos][i] != 0 &&
this->adjMatrix[i][vertPos] != 0) // вычисление соседей
nbrsList.push_back(this->vertList[i]); запись соседей в вектор
}
}
return nbrsList; возврат списка соседей
}
Метод void InsertVertex(const T& vertex)
Метод служит для добавления вершины. Проверяет, что вектор вершин не полон, и добавляет туда вершину vertex, ссылку на которую он получил.
Код метода void InsertVertex(const T& vertex):
template
void Graph
if (!this->IsFull()) {
this->vertList.push_back(vertex);
}
else {
cout << "Граф уже заполнен. Невозможно добавить новую вершину " << endl;
return;
}
}
Метод void InsertEdge(const T& vertex1, const T& vertex2)
Метод вставляет между вершинами vertex1 и vertex2 ребро весом weight (для взвешенного графа). Сначала проверяется, что vertex1 и vertex2 есть в векторе вершин, затем берутся их номера, и проверяется, что между ними еще нет ребра, если нет, то в матрицу смежности вставляется значение weight (или 1 – для невзвешенного графа), если есть, то выводится об этом сообщение на экран. Если граф ориентированный, то вставляется значение в матрицу смежности по индексам [vertPos1][vertPos2]. Если граф неориентированный, то еще вставляется значение по индексам [vertPos2][vertPos1]. Если граф невзвешенный, то третий параметр weight не нужен.
Код метода void InsertEdge(const T& vertex1, const T& vertex2) для взвешенного ориентированного графа:
template
void Graph
if (this->GetVertPos(vertex1) != (-1) && this->GetVertPos(vertex2) != (-1)) {
int vertPos1 = GetVertPos(vertex1);
int vertPos2 = GetVertPos(vertex2);
if (this->adjMatrix[vertPos1][vertPos2] != 0) {
cout << "Ребро между этими вершинами уже существует" << endl;
return;
}
else {
this->adjMatrix[vertPos1][vertPos2] = weight;
}
}
else {
cout << "Обеих вершин (или одной из них) нет в графе " << endl;
return;
}
}
Код метода void InsertEdge(const T& vertex1, const T& vertex2) для взвешенного неориентированного графа:
template
void Graph
if (this->GetVertPos(vertex1) != (-1) && this->GetVertPos(vertex2) != (-1)) {
int vertPos1 = GetVertPos(vertex1);
int vertPos2 = GetVertPos(vertex2);
if (this->adjMatrix[vertPos1][vertPos2] != 0
&& this->adjMatrix[vertPos2][vertPos1] != 0) {
cout << "Ребро между вершинами уже есть" << endl;
return;
}
else {
this->adjMatrix[vertPos1][vertPos2] = weight;
this->adjMatrix[vertPos2][vertPos1] = weight;
}
}
else {
cout << "Обеих вершин (или одной из них) нет в графе " << endl;
return;
}
}
Код метода void InsertEdge(const T& vertex1, const T& vertex2) для невзвешенного ориентированного графа:
template
void Graph
if (this->GetVertPos(vertex1) != (-1) && this->GetVertPos(vertex2) != (-1)) {
int vertPos1 = GetVertPos(vertex1);
int vertPos2 = GetVertPos(vertex2);
if (this->adjMatrix[vertPos1][vertPos2] != 0) {
cout << "Ребро между этими вершинами уже существует" << endl;
return;
}
else {
this->adjMatrix[vertPos1][vertPos2] = 1;
}
}
else {
cout << "Обеих вершин (или одной из них) нет в графе " << endl;
return;
}
}
Код метода void InsertEdge(const T& vertex1, const T& vertex2) для невзвешенного неориентированного графа:
template
void Graph
if (this->GetVertPos(vertex1) != (-1) && this->GetVertPos(vertex2) != (-1)) {
int vertPos1 = GetVertPos(vertex1);
int vertPos2 = GetVertPos(vertex2);
if (this->adjMatrix[vertPos1][vertPos2] != 0
&& this->adjMatrix[vertPos2][vertPos1] != 0) {
cout << "Ребро между этими вершинами уже существует" << endl;
return;
}
else {
this->adjMatrix[vertPos1][vertPos2] = 1;
this->adjMatrix[vertPos2][vertPos1] = 1;
}
}
else {
cout << "Обеих вершин (или одной из них) нет в графе " << endl;
return;
}
}
Метод void Print()
Этот метод используется для печати матрицы смежности графа. Самым первым печатается номер вершины, а затем значения из матрицы смежности для неё. Например, 3 0 1 0 1 будет означать, что вершина 3 не связана с вершинами 1 и 3, но связана с вершинами 2 и 4.
Код метода void Print():
template
void Graph
if (!this->IsEmpty()) {
cout << "Матрица смежности графа: " << endl;
for (int i = 0, vertListSize = this->vertList.size(); i < vertListSize; ++i) {
cout << this->vertList[i] << " ";
for (int j = 0; j < vertListSize; ++j) {
cout << " " << this->adjMatrix[i][j] << " ";
}
cout << endl;
}
}
else {
cout << "Граф пуст " << endl;
}
}
Рассмотрим следующие графы:
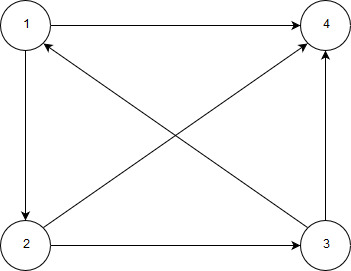
Рисунок 20 – Невзвешенный ориентированный граф
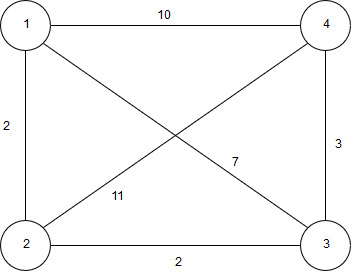
Рисунок 21 – Взвешенный неориентированный граф
Здесь выполняется ввод вершин графа и вызываются функции.
Далее будут рассмотрены невзвешенный ориентированный (рисунок 20) и взвешенный неориентированный (рисунок 21) графы (так как в остальных случаях функции выглядят также). Обе функции похожи, за исключением того, что для взвешенного графа еще требуется переменная веса.
В функции main() создается объект graph класса Graph типа int, а также объявляются переменные: amountVerts (количество вершин), amountEdges (количество ребер), vertex (вершина), sourceVertex, targetVertex (исходная и конечная вершины - sourceVertex это вершина, из которой ребро будет идти в вершину targetVertex), для взвешенного графа еще edgeWeight (вес ребра).
Затем пользователь вводит нужное ему количество вершин и ребер. После этого в цикле пользователь вводит вершины.
Объявляется и инициализируется указатель на вершину (инициализируется адресом введенной вершины), затем у объекта graph вызывается метод InsertVertex, куда передается вершина.
После этого цикла идет ввод ребер. Ввод ребер осуществляется также в цикле, пользователь вводит стартовую вершину, конечную вершину и вес ребра (для взвешенного графа), после того, как все данные введены, вызывается функция InsertEdge у объекта класса Graph с двумя или тремя параметрами (в зависимости от того, взвешенный граф или нет). После этого вызывается метод Print, и выводится матрица смежности.
После этого программа завершает работу.
vertPtr – vertexPointer - указатель на вершину, аналогично targetVertPtr - targetVertexPointer указатель на конечную(целевую) вершину, sourceVertPtr - указатель на исходную вершину.
Код файла main.cpp для невзвешенного ориентированного графа:
#include "Unweighted directed Graph.h"
#include
#include
#include
using namespace std;
int main() {
setlocale(LC_ALL, "Russian");
{
Graph
int amountVerts, amountEdges, vertex, sourceVertex, targetVertex; // создание необходимых для ввода графа переменных
cout << "Введите количество вершин графа: "; cin >> amountVerts; cout << endl; // ввод количества рёбер графа в переменную amountVerts
cout << "Введите количество ребер графа: "; cin >> amountEdges; cout << endl; // ввод количества рёбер графа в переменную amountEdges
for (int i = 0; i < amountVerts; ++i) {
cout << "Вершина: "; cin >> vertex; // ввод вершины
int* vertPtr = &vertex; // запоминаем адрес вершины с помощью указателя
graph.InsertVertex(*vertPtr); передаём ссылку на вершину в функцию InsertVertex; происходит вставка вершины в вектор вершин
cout << endl;
}
for (int i = 0; i < amountEdges; ++i) {
cout << "Исходная вершина: "; cin >> sourceVertex; cout << endl; // ввод исходной вершины
int* sourceVertPtr = &sourceVertex; // запоминаем адрес исходной вершины
cout << "Конечная вершина: "; cin >> targetVertex; cout << endl; // ввод вершины, до которой будет идти ребро от исходной вершины
int* targetVertPtr = &targetVertex; // запоминаем адрес конечной вершины (до которой будет идти ребро от исходной вершины)
graph.InsertEdge(*sourceVertPtr, *targetVertPtr); // вставка ребра между исходной и конечной вершинами, в функцию передаются ссылки на исходную и конечную вершины
}
cout << endl;
graph.Print(); // печать матрицы смежности графа
}
_getch();
return 0;
}
Файл main.cpp для взвешенного неориентированного графа:
#include "Weighted undirected Graph.h"
#include
#include
#include
using namespace std;
int main() {
setlocale(LC_ALL, "Russian");
{
Graph
int amountVerts, amountEdges, vertex, sourceVertex, targetVertex, edgeWeight; // создание необходимых для ввода графа переменных (добавилась переменная edgeWeight)
cout << "Введите количество вершин графа: "; cin >> amountVerts; cout << endl; // ввод количества рёбер графа в переменную amountVerts
cout << "Введите количество ребер графа: "; cin >> amountEdges; cout << endl; // ввод количества рёбер графа в переменную amountEdges
for (int i = 0; i < amountVerts; ++i) {
cout << "Вершина: "; cin >> vertex; ввод вершины
int* vertPtr = &vertex; // запоминаем адрес вершины с помощью указателя
graph.InsertVertex(*vertPtr); передаём ссылку на вершину в функцию InsertVertex; происходит вставка вершины в вектор вершин
cout << endl;
}
for (int i = 0; i < amountEdges; ++i) {
cout << "Исходная вершина: "; cin >> sourceVertex; cout << endl; // ввод исходной вершины
int* sourceVertPtr = &sourceVertex; // запоминаем адрес исходной вершины
cout << "Конечная вершина: "; cin >> targetVertex; cout << endl; // ввод вершины, до которой будет идти ребро от исходной вершины (ввод конечной вершины)
int* targetVertPtr = &targetVertex; // запоминаем адрес конечной вершины
cout << "Вес ребра: "; cin >> edgeWeight; cout << endl; // ввод числового значения веса ребра в переменную edgeWeight
graph.InsertEdge(*sourceVertPtr, *targetVertPtr, edgeWeight); // вставка ребра весом edgeWeight между исходной и конечной вершинами
}
cout << endl;
graph.Print(); // печать матрицы смежности
}
_getch();
return 0;
}
Результат работы программы:
Введите количество вершин графа: 4
Введите количество ребер графа: 6
Вершина: 1
Вершина: 2
Вершина: 3
Вершина: 4
Исходная вершина: 1
Конечная вершина: 2
Исходная вершина: 1
Конечная вершина: 4
Исходная вершина: 2
Конечная вершина: 4
Исходная вершина: 2
Конечная вершина: 3
Исходная вершина: 3
Конечная вершина: 4
Исходная вершина: 3
Конечная вершина: 1
Матрица смежности графа: // граф представлен на рисунке 20
1 0 1 0 1
2 0 0 1 1
3 1 0 0 1
4 0 0 0 0
Ещё один пример результата работы программы:
Введите количество вершин графа: 4
Введите количество ребер графа: 6
Вершина: 1
Вершина: 2
Вершина: 3
Вершина: 4
Исходная вершина: 1
Конечная вершина: 2
Вес ребра: 2
Исходная вершина: 1
Конечная вершина: 4
Вес ребра: 10
Исходная вершина: 2
Конечная вершина: 3
Вес ребра: 2
Исходная вершина: 3
Конечная вершина: 4
Вес ребра: 3
Исходная вершина: 3
Конечная вершина: 1
Вес ребра: 7
Исходная вершина: 2
Конечная вершина: 4
Вес ребра: 11
Матрица смежности графа: // граф представлен на рисунке 21
1 0 2 7 10
2 2 0 2 11
3 7 2 0 3
4 10 11 3 0
Алгоритмы обхода графов
Обход графа – процедура однократного посещения всех вершин.
Обход графа в глубину
Алгоритм обхода графа в глубину начинает выполнение с одной из вершин графа - начальной вершины, фиксирует информации о посещении этой вершины, и, перемещаясь по ребру, посещает соседние вершины. Обход графа в глубину применяется в различных расчётах на графах – например, в алгоритме Диница для поиска максимального потока в транспортной сети. Кроме того, правило левой руки при прохождении лабиринта (идти, ведя левой рукой по стенке) также является обходом в глубину. По завершении обхода все вершины окажутся пройдёнными - обработанными. Если при обходе встречается вершина, которая уже была пройдена, то повторной обработки делать не нужно.

Рисунок 22 – Алгоритм обхода графа в глубину
Обход начинается с вершины v0. Не важно, какая именно обработка выполняется на каждой вершине – может быть, выводится на печать метка вершины или выполняется более сложная процедура. После обработки вершины v0 выполняется переход по одному из ребер к одной из соседних вершин. В данном примере существуют две возможности: перейти к вершине v1 или к вершине v4. Итак, алгоритм обхода стоит перед выбором: перейти к вершине v1 или к вершине v4. Не имеет значения, как именно сделать этот выбор, - допустим, что выбрана вершина v1. После ее обработки рисунок будет выглядеть так:
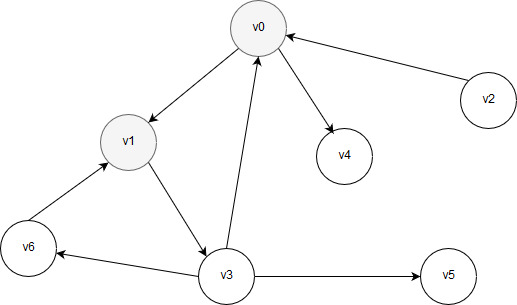
Рисунок 23 – Обработаны вершины v0 и v1
Затем алгоритм совершает переход к вершине, соседствующей с вершиной v1. Если соседняя вершина уже обработана, то алгоритм продвигается дальше, пропуская уже обработанные соседние вершины. В данном примере рассматривается только одна соседняя вершина v3 и обрабатывается. В данный момент обработанными являются три вершины, как показано ниже.
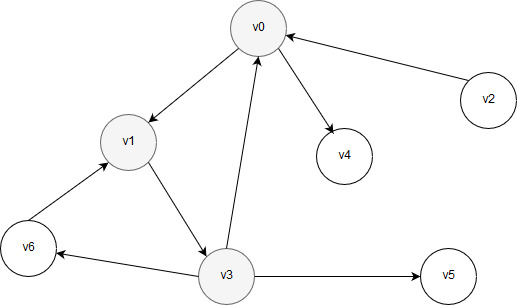
Рисунок 24 – Обработаны вершины v0, v1 и v3
Одной из соседних вершин по отношению к вершине v3 является вершина v0, однако она уже обработана. Таким образом, чтобы предотвратить зацикливание, переходить от вершины v3 в вершину v0 нельзя. Поэтому можно перейти к другому соседу: v5 или v6. Перейдем в вершину v5. После ее обработки на графе будут цветом отмечены вершины v0 и v1 как посещённые:
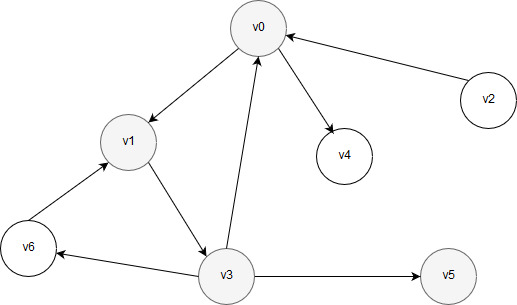
Рисунок 25 – Обработаны вершины v0, v1, v3 и v5
Поскольку у вершины v5 нет соседних вершин, дальнейший поиск в глубину невозможен. Далее, алгоритм возвращается назад и проверяет, нет ли у предыдущей вершины v3 других необработанных соседних вершин. У вершины v3 есть ещё необработанная соседняя вершина v6. Выполняется переход в вершину v6 и обработка вершины v6. После обработки вершины v6 рисунок имеет следующий вид:
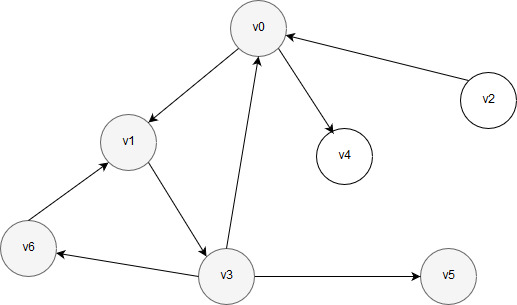
Рисунок 26 – Вершина v6 обработана после возврата к вершине v3
У вершины v6 есть соседняя вершина – v1, однако она уже обработана. Таким образом, у вершины v6 нет обработанных соседних вершин, поэтому обход возвращается назад – в вершину v3, чтобы проверить, остались ли у нее другие необработанные соседи. У вершины v3 больше нет необработанных соседей. Значит, алгоритм возвращается к предыдущей вершине v1, чтобы проверить, есть ли у нее непомеченные соседние вершины. У вершины v1 нет необработанных соседних вершин, поэтому выполняется возврат в вершину v0 для проверки, есть ли у вершины v0 необработанные соседи. Такой сосед есть – это вершина v4, поэтому алгоритм переходит в нее. После перехода граф выглядит так:
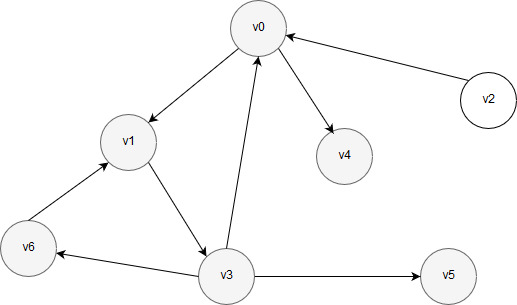
Рисунок 27 – Вершина v4 обработана
У вершины v4 соседних вершин нет, поэтому происходит возврат в вершину v0. У вершины v0 больше нет необработанных соседних вершин. Поскольку вершина v0 была отправной точкой нашего обхода, дальнейшее перемещение по графу невозможно (из вершины v0 в вершину v2 попасть невозможно). Обход графа завершен.
Во время обхода графа в глубину обрабатываются лишь те вершины, которые достижимы из начальной вершины графа. Существует еще одно важное свойство обхода графа в глубину: из начальной вершины осуществляется переход в соседнюю вершину, оттуда – в соседнюю к соседней и так далее – при этом обход графа осуществляется настолько глубоко, насколько это возможно, и только потом выполняется возврат в исходную вершину. Таким образом, алгоритм обхода графа в глубину работает рекурсивно[8].
Рассмотрим программную реализацию обхода графа в глубину.
В заголовочном файле появится массив посещенных вершин bool *visitedVerts = new bool[20], о нём будет рассказано позже. Алгоритм обхода графа в глубину выполняет функция void DFS(T& startVertex, bool *visitedVerts).
Она принимает в качестве входных параметров ссылку на вершину, из которой начать обход графа и указатель на первый элемент массива из логических значений. В этом массиве индекс каждой вершины соответствует индексу вершины в векторе вершин vertList. Если в visitedVerts элемент по какому-либо индексу указывает на 1, это значит, что вершина по этому индексу уже посещена. Например, если *visitedVerts[0] = 1, то вершина vertList[0] уже обработана. С помощью массива visitedVerts помечаются посещенные вершины.
Как только выполнение программы переходит в функцию, происходит следующее:
-
Выводится сообщение о том, что вершина startVertex посещена. -
В массиве visitedVerts по индексу вершины startVertex в векторе vertList устанавливается значение true (вершина посещена). -
Создается вектор вершин, соседних с startVertex, в него записываются соседи startVertex с помощью функции GetNbrs. -
Работает цикл с параметром. Он работает, пока значение переменной цикла меньше размера вектора соседей startVertex. В цикле осуществляется проверка, что вершина по индексу i (переменная цикла) в векторе соседей не посещена (то есть что в массиве visitedVerts по индексу this->GetVertPos(neighbors[i]) стоит не значение true). Если это так, то функция DFS вызывается для соседа neighbors[i]. В функцию передается этот сосед и наш массив visitedVerts.
Затем алгоритм повторится уже для соседа. На экран выведется сообщение, что сосед посещен, в visitedVerts записывается значение true по нужному индексу, а затем для соседей переданного в функцию соседа выполняются те же действия. Как только у кого-то не окажется соседей, пойдет возврат из рекурсии.
В функции main() после печати графа добавится несколько строк – ввод стартовой вершины и вызов функции DFS().
Код метода void DFS(T& startVertex, bool *visitedVerts):
template
void Graph
cout << "Вершина " << startVertex << " посещена" << endl; // выводим сообщение о том, что вершина посещена
visitedVerts[this->GetVertPos(startVertex)] = true; // отмечаем в массиве посещенных вершин, что вершина посещена
std::vector
for (int i = 0, size = this->GetNbrs(startVertex).size(); i < size; ++i) {
if (visitedVerts[this->GetVertPos(neighbors[i])] != true)
this->DFS(neighbors[i], visitedVerts); // в цикле проверяем, что соседи текущей вершины ещё не посещены и вызываем функцию обхода графа в глубину
}
}
Код файла main.cpp:
#include "Unweighted directed Graph.h"
#include
#include
#include
using namespace std;
int main() {
setlocale(LC_ALL, "Russian");
{
Graph
int amountVerts, amountEdges, vertex, sourceVertex, targetVertex; // создание необходимых для ввода графа переменных
cout << "Введите количество вершин графа: "; cin >> amountVerts; cout << endl; // ввод количества вершин в переменную amountVerts
cout << "Введите количество ребер графа: "; cin >> amountEdges; cout << endl; // ввод количества рёбер в переменную amountEdges
for (int i = 0; i < amountVerts; ++i) {
cout << "Вершина: "; cin >> vertex; // ввод вершины
int* vertPtr = &vertex; // запоминаем адрес вершины с помощью указателя
graph.InsertVertex(*vertPtr); // вставка вершины в вектор вершин с помощью функции InsertVertex, в функцию передается ссылка на введенную вершину
cout << endl;
}
for (int i = 0; i < amountEdges; ++i) {
cout << "Исходная вершина: "; cin >> sourceVertex; cout << endl; // ввод исходной вершины в переменную sourceVertex
int* sourceVertPtr = &sourceVertex; // запоминаем адрес исходной вершины
cout << "Конечная вершина: "; cin >> targetVertex; cout << endl; // ввод конечной вершины (вершины, до которой идет ребро от исходной) в переменную targetVertex
int* targetVertPtr = &targetVertex; // запоминаем адрес конечной вершины
graph.InsertEdge(*sourceVertPtr, *targetVertPtr); // вставка ребра между исходной и конечной вершинами с помощью функции InsertEdge, в которую передаются ссылки на исходную и конечную вершины
}
cout << endl;
graph.Print(); // печать матрицы смежности графа
cout << "Введите вершину, с которой начать обход: "; cin >> vertex; cout << endl; // ввод начальной вершины, с которой начнется обход графа в глубину (в нашем случае это 0)
int* vertPtr = &vertex; // запоминаем адрес введенной вершины
graph.DFS(*vertPtr, visitedVerts); вызываем функцию обхода графа в глубину, в функцию передаются ссылка на введенную вершину и вектор посещенных вершин
}
В качестве результата приведена матрица смежности и выведенные сообщения во время выполнения метода DFS, поскольку ввод данных был продемонстрирован ранее.
Матрица смежности графа: // граф представлен на рисунке 22
0 0 1 0 0 1 0 0
1 0 0 0 1 0 0 0
2 1 0 0 0 0 0 0
3 1 0 0 0 0 1 1
4 0 0 0 0 0 0 0
5 0 0 0 0 0 0 0
6 0 0 0 0 0 0 0
Введите вершину, с которой начать обход: 0
Вершина 0 посещена
Вершина 1 посещена
Вершина 3 посещена
Вершина 5 посещена
Вершина 6 посещена
Вершина 4 посещена