ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 46
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Обход графа в ширину
Существует еще один алгоритм обхода графа – обход в ширину (англ. Breadth First Search). Этот алгоритм использует очередь для отслеживания необработанных соседних вершин. Этот алгоритм обхода графа применяется для поиска компонент связности в графе, а так же, как и алгоритм обхода в глубину, применяется при прохождении лабиринтов. Поиск начинается с начальной вершины, которая обрабатывается, маркируется и помещается в очередь. Возьмем для примера граф, рассмотренный на рисунке 22(с прошлого раздела):
Предположим, что начальной является вершина v0. Тогда вершина является первой вершиной, подлежащей обработке, маркировке цветом и сохранению в очереди.
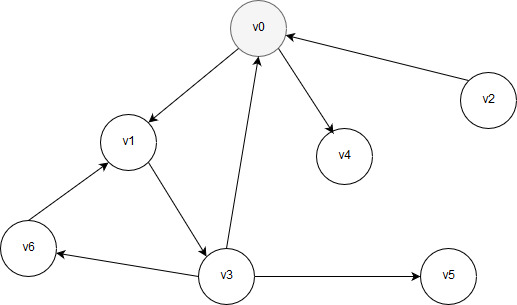

Рисунок 28 – Вершина v0 промаркирована и занесена в очередь
На данный момент в голове очереди находится начальная вершина v0.
После того, как начальная вершина обработана, промаркирована и помещена в очередь, начинается выполнение основной части алгоритма обхода графа в ширину. Основой алгоритма является циклический процесс, в котором обработанная вершина удаляется из очереди, а в очередь помещаются соседствующие с обработанной вершины. Таким образом, тело цикла состоит из двух основных шагов:
-
Удалить вершину v из головы очереди -
Для каждой непомеченной вершины u, соседней по отношению к вершине v, обработать вершину u, маркировать ее и поместить в очередь (вершина u может иметь соседние необработанные вершины).
Эти действия выполняются до тех пор, пока очередь не станет пустой.
Рассмотрим работу алгоритма на примере, когда вершина v0 находится в голове очереди. Вершина v0 удаляется из очереди и отмечается, что у нее остались необработанными две соседние вершины – v1 и v4. Каждая из них обрабатывается, маркируется и помещается в очередь. Допустим, сначала в очередь поставлена вершина v1, а затем вершина v4 (очередность может быть любой, вершина v4 может быть поставлена первой, а вершина v1 за ней – алгоритм будет работать корректно в любом случае). После того, как вершины v1 и v4 были поставлены в очередь, граф выглядит следующим образом:
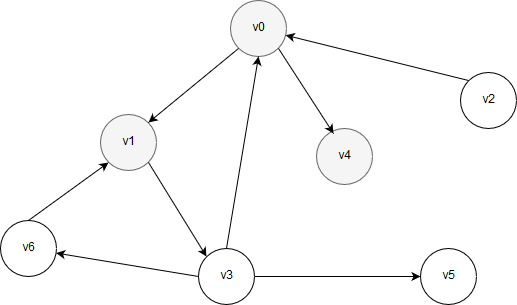

Рисунок 29 – Промаркированы вершины v0, v1, v4, в очереди находятся вершины v1 и v4
Поскольку очередь не пуста, два шага выполняются снова: первый элемент (вершина v1) удаляется, обрабатывается, все необработанные соседние вершины маркируются и помещаются в очередь. Единственным неотмеченным соседом вершины v1 является вершина v3, поэтому после обработки, маркировки и постановки в очередь вершины v3 граф выглядит так:
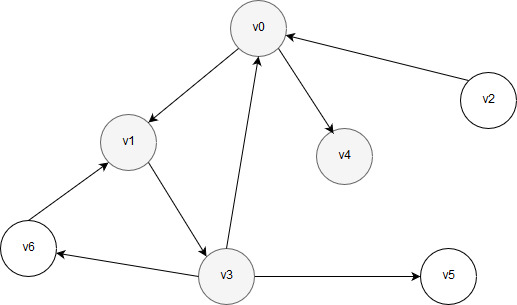

Рисунок 30 – Промаркированы вершины v0, v1, v4, v3, в очереди находятся вершины v3 и v4
Далее из головы очереди удаляется вершина v4. Поскольку у нее нет соседних вершин, никакие вершины больше не обрабатываются и не становятся в очередь, при этом граф выглядит так:


Рисунок 31 - Промаркированы вершины v0, v1, v4, v3, в очереди находится только вершина v3
Следующей из очереди удаляется вершина v3. У нее есть две непомеченные соседние вершины (вершины v5 и v6), которые обрабатываются, маркируются и помещаются в очередь. Граф выглядит следующим образом:


Рисунок 32 – Промаркированы вершины v0, v1, v4, v3, v5, v6, в очереди находятся вершины v5 и v6
Вершина v0 не обрабатывается повторно, так как она уже помечена.
Результат обхода графа в глубину и в ширину одинаков – отличается порядок обработки. Вершины v0, v1, v3, v4, v5 и v6 обработаны, поскольку все они достижимы из начальной точки (вершины 0). Вершина v2 не обрабатывается, поскольку не существует пути из вершины v0 в вершину v2. При обходе графа в ширину вершины обрабатываются в следующем порядке: сначала вершина v0, потом v1 и v4, затем обрабатываются их соседи (вершина v3) и так далее. При обходе графа в глубину сначала обрабатываются вершины v0, v1, v3 и v5 [8].
Рассмотрим программную реализацию обхода графа в ширину.
Она, как и функция DFS, принимает в качестве входных параметров вершину, с которой надо начать обход графа и массив значений булева типа для вершины (посещена или нет вершина по определенному индексу; индекс в массиве visitedVerts совпадает с номером вершины в векторе вершин). Кроме того, в описании класса появляется очередь std::queue
Когда выполнение программы переходит внутрь функции BFS, выполняется проверка, является ли посещенной вершина startVertex. Если ее еще не посещали, то она заносится в очередь, затем на экран выводится сообщение о том, что вершина обработана и в массиве visitedVerts для нее устанавливается значение true. Если вершина обработана, ничего не происходит, управление передается следующим операторам программы: выделяются соседи вершины startVertex, из очереди удаляется голова, затем в цикле для всех соседей выполняются следующие действия.
-
Выполняется проверка, посещен ли сосед -
Если не посещен, то эта соседняя вершина помещается в очередь и на экран выводится сообщение о том, что вершина обработана
После работы этого цикла, работает следующий цикл:
-
Пока очередь не пуста, циклически вызывается функция BFS, в которую в качестве начальной вершины передается головная вершина очереди -
В функции main() после ввода всех вершин и ребер пользователь вводит начальную вершину и вызывается функция BFS.
Код функции void BFS(T& startVertex, bool *visitedVerts):
template
void Graph
if (visitedVerts[this->GetVertPos(startVertex)] == false) { // проверяем, была ли ранее посещена вершина startVertex
this->VertsQueue.push(startVertex); // если startVertex ещё не была посещена, то она заносится в очередь вершин VertsQueue
cout << "Вершина " << startVertex << " обработана" << endl; // выводится сообщение, что startVertex теперь посещена
visitedVerts[this->GetVertPos(startVertex)] = true; // в массиве посещенных вершин отмечаем, что вершина по индексу, который на данный момент имеет startVertex, является посещенной
}
std::vector
this->VertsQueue.pop(); // удаляем голову очереди
for (int i = 0, size = neighbors.size(); i < size; ++i) {
if (visitedVerts[this->GetVertPos(neighbors[i])] != true) {
this->VertsQueue.push(neighbors[i]); // в цикле проверяем, посещен ли сосед вершины startVertex, если он еще не посещен, то он помещается в очередь вершин VertsQueue
visitedVerts[this->GetVertPos(neighbors[i])] = true; // а также он помещается в массив посещенных вершин
cout << "Вершина " << neighbors[i] << " обработана" << endl; // затем на экран выводится сообщение, что соседняя вершина обработана
}
}
while (!this->VertsQueue.empty()) {
this->BFS(this->VertsQueue.front(), visitedVerts); // в цикле вызывается функция обхода графа в ширину до тех пор, пока в очереди есть вершины
}
}
Код файла main.cpp:
#include "Unweighted directed Graph.h"
#include
#include
#include
using namespace std;
int main() {
setlocale(LC_ALL, "Ru");
{
Graph
int amountVerts, amountEdges, vertex, sourceVertex, targetVertex; // создание необходимых для ввода графа переменных
cout << "Введите количество вершин графа: "; cin >> amountVerts; cout << endl; // ввод количества вершин в переменную amountVerts
cout << "ВВедите количество ребер: "; cin >> amountEdges; cout << endl; // ввод количества рёбер в переменную amountEdges
for (int i = 0; i < amountVerts; ++i) {
cout << "Вершина: "; cin >> vertex; // ввод вершины
int* VertPtr = &vertex; // запоминаем адрес вершины с помощью указателя
graph.InsertVertex(*VertPtr); // вставка вершины в вектор вершин с помощью функции InsertVertex, в функцию передается ссылка на введенную вершину
cout << endl;
}
for (int i = 0; i < amountEdges; ++i) {
cout << "Исходная вершина: "; cin >> sourceVertex; cout << endl; // ввод исходной вершины в переменную sourceVertex
int* sourceVertPtr = &sourceVertex; // запоминаем адрес исходной вершины
cout << "Конечная вершина: "; cin >> targetVertex; cout << endl; // ввод конечной вершины (вершины, до которой идет ребро от исходной) в переменную targetVertex
int* targetVertPtr = &targetVertex; // запоминаем адрес конечной вершины
graph.InsertEdge(*sourceVertPtr, *targetVertPtr); // вставка ребра между исходной и конечной вершинами с помощью функции InsertEdge, в которую передаются ссылки на исходную и конечную вершины
}
cout << endl;
graph.Print(); // печать матрицы смежности
cout << "Введите вершину, с которой нужно начать обход: "; cin >> vertex; cout << endl; // ввод начальной вершины, с которой начнется обход графа в ширину (в нашем случае это 0)
int* VertPtr = &vertex; // запоминаем адрес введенной вершины
graph.BFS(*VertPtr, visitedVerts); вызываем функцию обхода графа в ширину, в функцию передаются ссылка на введенную вершину и вектор посещенных вершин
}
_getch();
return 0;
}
Результат работы программы:
Матрица смежности графа: // граф представлен на рисунки 22
0 0 1 0 0 1 0 0
1 0 0 0 1 0 0 0
2 1 0 0 0 0 0 0
3 1 0 0 0 0 1 1
4 0 0 0 0 0 0 0
5 0 0 0 0 0 0 0
6 0 0 0 0 0 0 0
Введите вершину, с которой начать обход: 0
Вершина 0 обработана
Вершина 1 обработана
Вершина 4 обработана
Вершина 3 обработана
Вершина 5 обработана
Вершина 6 обработана